Menu Close

Question-67564

Tinku Tara 0 Comments
Pin




Question Number 67564 by azizullah last updated on 28/Aug/19
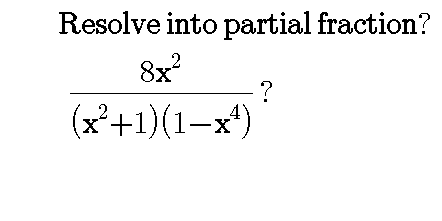
Commented by mathmax by abdo last updated on 28/Aug/19
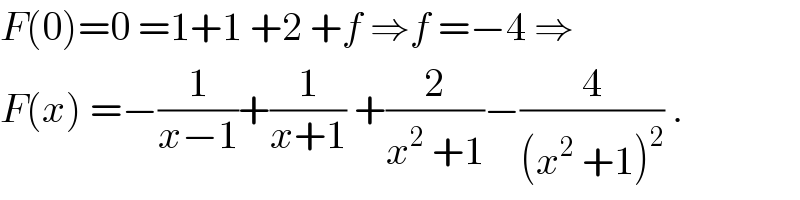
F(0)=0 =1+1 +2 +f ⇒f =−4 ⇒ F(x) =−(1/(x−1))+(1/(x+1)) +(2/(x^2 +1))−(4/((x^2 +1)^2 )) .
$${F}\left(\mathrm{0}\right)=\mathrm{0}\:=\mathrm{1}+\mathrm{1}\:+\mathrm{2}\:+{f}\:\Rightarrow{f}\:=−\mathrm{4}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=−\frac{\mathrm{1}}{{x}−\mathrm{1}}+\frac{\mathrm{1}}{{x}+\mathrm{1}}\:+\frac{\mathrm{2}}{{x}^{\mathrm{2}} \:+\mathrm{1}}−\frac{\mathrm{4}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:. \\ $$
Commented by mathmax by abdo last updated on 28/Aug/19
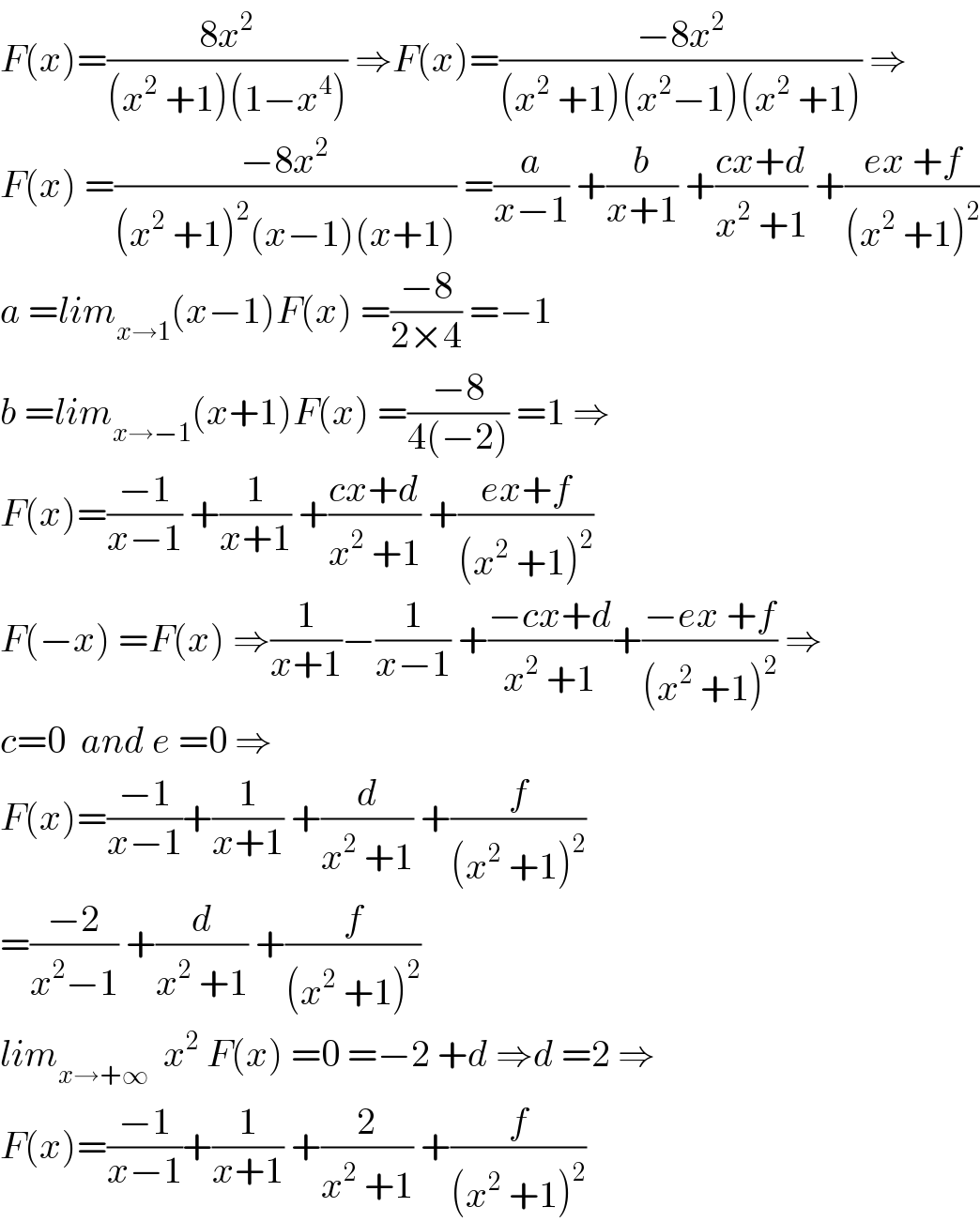
F(x)=((8x^2 )/((x^2 +1)(1−x^4 ))) ⇒F(x)=((−8x^2 )/((x^2 +1)(x^2 −1)(x^2 +1))) ⇒ F(x) =((−8x^2 )/((x^2 +1)^2 (x−1)(x+1))) =(a/(x−1)) +(b/(x+1)) +((cx+d)/(x^2 +1)) +((ex +f)/((x^2 +1)^2 )) a =lim_(x→1) (x−1)F(x) =((−8)/(2×4)) =−1 b =lim_(x→−1) (x+1)F(x) =((−8)/(4(−2))) =1 ⇒ F(x)=((−1)/(x−1)) +(1/(x+1)) +((cx+d)/(x^2 +1)) +((ex+f)/((x^2 +1)^2 )) F(−x) =F(x) ⇒(1/(x+1))−(1/(x−1)) +((−cx+d)/(x^2 +1))+((−ex +f)/((x^2 +1)^2 )) ⇒ c=0 and e =0 ⇒ F(x)=((−1)/(x−1))+(1/(x+1)) +(d/(x^2 +1)) +(f/((x^2 +1)^2 )) =((−2)/(x^2 −1)) +(d/(x^2 +1)) +(f/((x^2 +1)^2 )) lim_(x→+∞) x^2 F(x) =0 =−2 +d ⇒d =2 ⇒ F(x)=((−1)/(x−1))+(1/(x+1)) +(2/(x^2 +1)) +(f/((x^2 +1)^2 ))
$${F}\left({x}\right)=\frac{\mathrm{8}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{1}−{x}^{\mathrm{4}} \right)}\:\Rightarrow{F}\left({x}\right)=\frac{−\mathrm{8}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\frac{−\mathrm{8}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)}\:=\frac{{a}}{{x}−\mathrm{1}}\:+\frac{{b}}{{x}+\mathrm{1}}\:+\frac{{cx}+{d}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{ex}\:+{f}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${a}\:={lim}_{{x}\rightarrow\mathrm{1}} \left({x}−\mathrm{1}\right){F}\left({x}\right)\:=\frac{−\mathrm{8}}{\mathrm{2}×\mathrm{4}}\:=−\mathrm{1} \\ $$$${b}\:={lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right){F}\left({x}\right)\:=\frac{−\mathrm{8}}{\mathrm{4}\left(−\mathrm{2}\right)}\:=\mathrm{1}\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{−\mathrm{1}}{{x}−\mathrm{1}}\:+\frac{\mathrm{1}}{{x}+\mathrm{1}}\:+\frac{{cx}+{d}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{ex}+{f}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${F}\left(−{x}\right)\:={F}\left({x}\right)\:\Rightarrow\frac{\mathrm{1}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{{x}−\mathrm{1}}\:+\frac{−{cx}+{d}}{{x}^{\mathrm{2}} \:+\mathrm{1}}+\frac{−{ex}\:+{f}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${c}=\mathrm{0}\:\:{and}\:{e}\:=\mathrm{0}\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{−\mathrm{1}}{{x}−\mathrm{1}}+\frac{\mathrm{1}}{{x}+\mathrm{1}}\:+\frac{{d}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{f}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{1}}\:+\frac{{d}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{f}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${lim}_{{x}\rightarrow+\infty} \:\:{x}^{\mathrm{2}} \:{F}\left({x}\right)\:=\mathrm{0}\:=−\mathrm{2}\:+{d}\:\Rightarrow{d}\:=\mathrm{2}\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{−\mathrm{1}}{{x}−\mathrm{1}}+\frac{\mathrm{1}}{{x}+\mathrm{1}}\:+\frac{\mathrm{2}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{f}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Commented by Rasheed.Sindhi last updated on 29/Aug/19
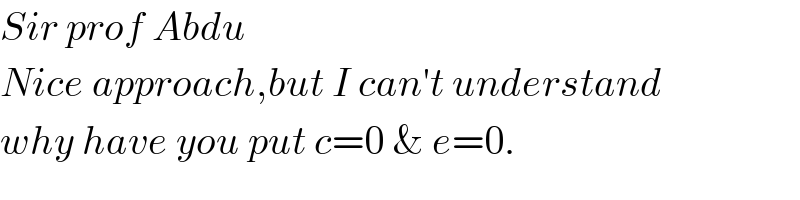
Sir prof Abdu Nice approach,but I can′t understand why have you put c=0 & e=0.
$${Sir}\:{prof}\:{Abdu} \\ $$$${Nice}\:{approach},{but}\:{I}\:{can}'{t}\:{understand} \\ $$$${why}\:{have}\:{you}\:{put}\:{c}=\mathrm{0}\:\&\:{e}=\mathrm{0}. \\ $$
Commented by mathmax by abdo last updated on 29/Aug/19
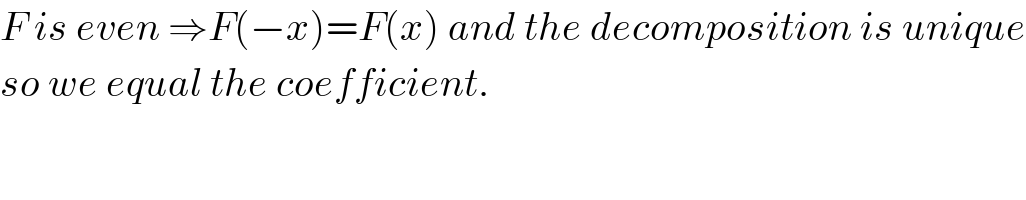
F is even ⇒F(−x)=F(x) and the decomposition is unique so we equal the coefficient.
$${F}\:{is}\:{even}\:\Rightarrow{F}\left(−{x}\right)={F}\left({x}\right)\:{and}\:{the}\:{decomposition}\:{is}\:{unique} \\ $$$${so}\:{we}\:{equal}\:{the}\:{coefficient}. \\ $$
Commented by Rasheed.Sindhi last updated on 29/Aug/19
ThαnX A L♥⊤ ∫!⋎.
$$\mathcal{T}{h}\alpha{n}\mathcal{X}\:\mathcal{A}\:\mathcal{L}\heartsuit\top\:\int!\curlyvee. \\ $$
Commented by azizullah last updated on 29/Aug/19
Thanks so much
$$\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{Thanks}}\:\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{much}} \\ $$
Commented by Abdo msup. last updated on 30/Aug/19
you are welcome
$${you}\:{are}\:{welcome} \\ $$
Commented by azizullah last updated on 13/Sep/19
excuse me sur! i need all theorems proof of class 9th. can you send me? i share it in our note.
$$\boldsymbol{\mathrm{excuse}}\:\boldsymbol{\mathrm{me}}\:\boldsymbol{\mathrm{sur}}!\:\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{need}}\:\boldsymbol{\mathrm{all}}\:\boldsymbol{\mathrm{theorems}}\:\boldsymbol{\mathrm{proof}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{class}}\:\mathrm{9}\boldsymbol{\mathrm{th}}. \\ $$$$\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{send}}\:\boldsymbol{\mathrm{me}}?\:\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{share}}\:\boldsymbol{\mathrm{it}}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{our}}\:\boldsymbol{\mathrm{note}}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *