Menu Close

Given-a-10-digit-number-X-1345789026-How-many-10-digit-number-that-can-be-made-using-every-digit-from-X-with-condition-If-a-number-n-is-located-in-k-th-position-of-X-then-the-new-created-numb

Tinku Tara 0 Comments
Pin




Question Number 88876 by Joel578 last updated on 13/Apr/20
Given a 10−digit number X = 1345789026 How many 10−digit number that can be made using every digit from X, with condition: If a number n is located in k^(th) position of X, then the new created number must not contain number n in k^(th) position Example: • Number 1 is located in 1^(st) position of X, hence 1234567890 is not valid, but 2134567890 is valid • Number 5 and 0 are located in 4^(th) and 8^(th) position of X, hence 9435162087 is not valid, but 9431506287 is valid. • 1345026789 is not valid • and so on...
$$\mathrm{Given}\:\mathrm{a}\:\mathrm{10}−\mathrm{digit}\:\mathrm{number}\:{X}\:=\:\mathrm{1345789026} \\ $$$$\mathrm{How}\:\mathrm{many}\:\mathrm{10}−\mathrm{digit}\:\mathrm{number}\:\mathrm{that}\:\mathrm{can}\:\mathrm{be}\:\mathrm{made} \\ $$$$\mathrm{using}\:\mathrm{every}\:\mathrm{digit}\:\mathrm{from}\:{X},\:\mathrm{with}\:\mathrm{condition}: \\ $$$$\mathrm{If}\:\mathrm{a}\:\mathrm{number}\:{n}\:\:\mathrm{is}\:\mathrm{located}\:\mathrm{in}\:{k}^{{th}} \:\mathrm{position}\:\mathrm{of}\:{X},\:\mathrm{then} \\ $$$$\mathrm{the}\:\mathrm{new}\:\mathrm{created}\:\mathrm{number}\:\mathrm{must}\:\mathrm{not}\:\mathrm{contain} \\ $$$$\mathrm{number}\:{n}\:\mathrm{in}\:{k}^{{th}} \:\mathrm{position} \\ $$$$ \\ $$$$\mathrm{Example}: \\ $$$$\bullet\:\mathrm{Number}\:\mathrm{1}\:\mathrm{is}\:\mathrm{located}\:\mathrm{in}\:\mathrm{1}^{{st}} \:\mathrm{position}\:\mathrm{of}\:{X},\:\mathrm{hence} \\ $$$$\mathrm{1234567890}\:\mathrm{is}\:\mathrm{not}\:\mathrm{valid},\:\mathrm{but}\:\mathrm{2134567890} \\ $$$$\mathrm{is}\:\mathrm{valid} \\ $$$$\bullet\:\mathrm{Number}\:\mathrm{5}\:\mathrm{and}\:\mathrm{0}\:\mathrm{are}\:\mathrm{located}\:\mathrm{in}\:\mathrm{4}^{{th}} \:\mathrm{and}\:\mathrm{8}^{{th}} \:\mathrm{position} \\ $$$$\mathrm{of}\:{X},\:\mathrm{hence}\:\mathrm{9435162087}\:\mathrm{is}\:\mathrm{not}\:\mathrm{valid},\:\mathrm{but} \\ $$$$\mathrm{9431506287}\:\mathrm{is}\:\mathrm{valid}. \\ $$$$\bullet\:\mathrm{1345026789}\:\mathrm{is}\:\mathrm{not}\:\mathrm{valid} \\ $$$$\bullet\:\mathrm{and}\:\mathrm{so}\:\mathrm{on}… \\ $$
Commented by Joel578 last updated on 13/Apr/20
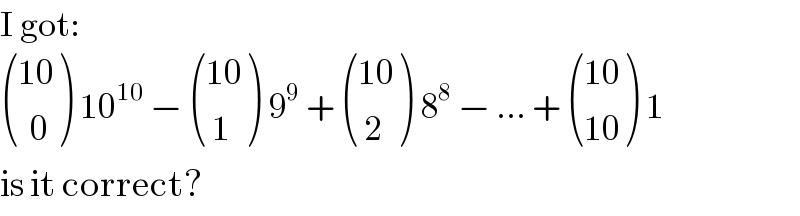
I got: (((10)),(( 0)) ) 10^(10) − (((10)),(( 1)) ) 9^9 + (((10)),(( 2)) ) 8^8 − ... + (((10)),((10)) ) 1 is it correct?
$$\mathrm{I}\:\mathrm{got}: \\ $$$$\begin{pmatrix}{\mathrm{10}}\\{\:\:\mathrm{0}}\end{pmatrix}\:\mathrm{10}^{\mathrm{10}} \:−\:\begin{pmatrix}{\mathrm{10}}\\{\:\mathrm{1}}\end{pmatrix}\:\mathrm{9}^{\mathrm{9}} \:+\:\begin{pmatrix}{\mathrm{10}}\\{\:\mathrm{2}}\end{pmatrix}\:\mathrm{8}^{\mathrm{8}} \:−\:…\:+\:\begin{pmatrix}{\mathrm{10}}\\{\mathrm{10}}\end{pmatrix}\:\mathrm{1} \\ $$$$\mathrm{is}\:\mathrm{it}\:\mathrm{correct}? \\ $$
Commented by mr W last updated on 29/Mar/21
(8/9)×!10=1 186 632
$$\frac{\mathrm{8}}{\mathrm{9}}×!\mathrm{10}=\mathrm{1}\:\mathrm{186}\:\mathrm{632} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *