Question Number 67623 by mr W last updated on 29/Aug/19

Commented by mr W last updated on 29/Aug/19
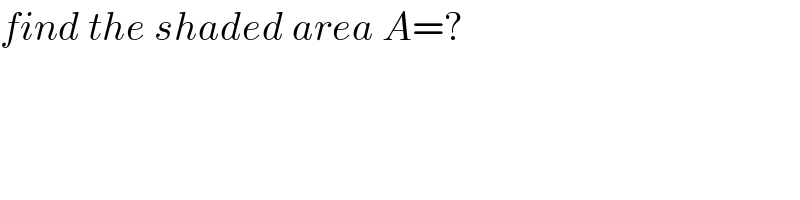
$${find}\:{the}\:{shaded}\:{area}\:{A}=? \\ $$
Commented by Prithwish sen last updated on 29/Aug/19

$$\because\mathrm{AL}\:\mathrm{is}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{bisector} \\ $$$$\therefore\:\mathrm{AL}\:=\sqrt{\mathrm{7}×\mathrm{8}\left[\mathrm{1}−\left(\frac{\mathrm{9}}{\mathrm{7}+\mathrm{8}}\right)^{\mathrm{2}} \right.}\:=\:\frac{\mathrm{8}\sqrt{\mathrm{14}}}{\mathrm{5}}\:\backsim\:\mathrm{6} \\ $$$$\mathrm{CL}=\:\mathrm{s}−\mathrm{c}\:=\:\left(\frac{\mathrm{7}+\mathrm{8}+\mathrm{9}}{\mathrm{2}}\right)−\mathrm{8}\:=\:\mathrm{4}\:=\:\mathrm{CD} \\ $$$$\mathrm{Let}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{be}\:\mathrm{R} \\ $$$$\therefore\:\mathrm{From}\:\bigtriangleup\mathrm{AOD} \\ $$$$\left(\mathrm{R}+\mathrm{6}\right)^{\mathrm{2}} =\:\mathrm{R}^{\mathrm{2}} +\left(\mathrm{4}+\mathrm{7}\right)^{\mathrm{2}} \Rightarrow\mathrm{R}=\:\mathrm{7}.\mathrm{08}\:\left(\mathrm{approx}\right) \\ $$$$\mathrm{Area}\:\mathrm{of}\:\mathrm{LODC}\:=\:\mathrm{4}×\mathrm{7}.\mathrm{08}\:\backsim\:\mathrm{28}.\mathrm{32} \\ $$$$\mathrm{Now}\:\angle\mathrm{DCO}\:=\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{OD}}{\mathrm{DC}}\:=\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{7}.\mathrm{08}}{\mathrm{4}}\:\backsim\:\mathrm{60}^{°} \\ $$$$\therefore\:\angle\mathrm{COD}\:=\:\mathrm{30}^{°} \\ $$$$\therefore\angle\mathrm{LOD}\:=\:\mathrm{60}^{°} \\ $$$$\therefore\:\mathrm{Area}\:\mathrm{of}\:\mathrm{sector}\:\mathrm{OLD}\:=\:\left(\mathrm{7}.\mathrm{08}\right)^{\mathrm{2}} ×\pi×\frac{\mathrm{60}}{\mathrm{360}}\:\backsim\:\mathrm{26}.\mathrm{25} \\ $$$$\therefore\:\boldsymbol{\mathrm{Area}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{shaded}}\:\boldsymbol{\mathrm{portion}}\:=\mathrm{28}.\mathrm{32}−\mathrm{26}.\mathrm{25}=\mathrm{2}.\mathrm{07} \\ $$$$\boldsymbol{\mathrm{S}}\mathrm{ir}\:\mathrm{waiting}\:\mathrm{for}\:\mathrm{your}\:\mathrm{valuable}\:\mathrm{response}. \\ $$
Commented by Prithwish sen last updated on 29/Aug/19
Commented by mr W last updated on 29/Aug/19
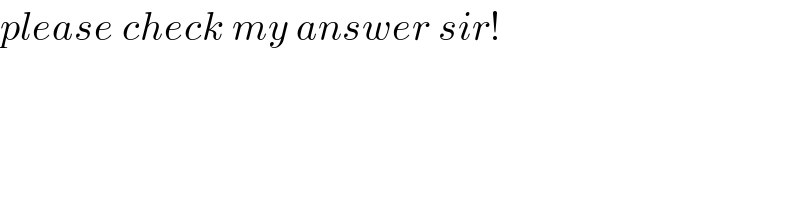
$${please}\:{check}\:{my}\:{answer}\:{sir}! \\ $$
Commented by Prithwish sen last updated on 29/Aug/19

$$\mathrm{Your}\:\mathrm{solution}\:\mathrm{makes}\:\mathrm{the}\:\mathrm{problem}\:\mathrm{so}\:\mathrm{simple}. \\ $$$$\mathrm{You}\:\mathrm{just}\:\mathrm{have}\:\mathrm{an}\:\mathrm{extraordinary}\:\mathrm{creative} \\ $$$$\mathrm{mind}.\:\mathrm{Everyday}\:\mathrm{I}\:\mathrm{am}\:\mathrm{learning}\:\mathrm{something}\: \\ $$$$\mathrm{new}\:\mathrm{from}\:\mathrm{you}.\:\mathrm{Thanks}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{sir}. \\ $$
Answered by mr W last updated on 29/Aug/19
Commented by mr W last updated on 29/Aug/19
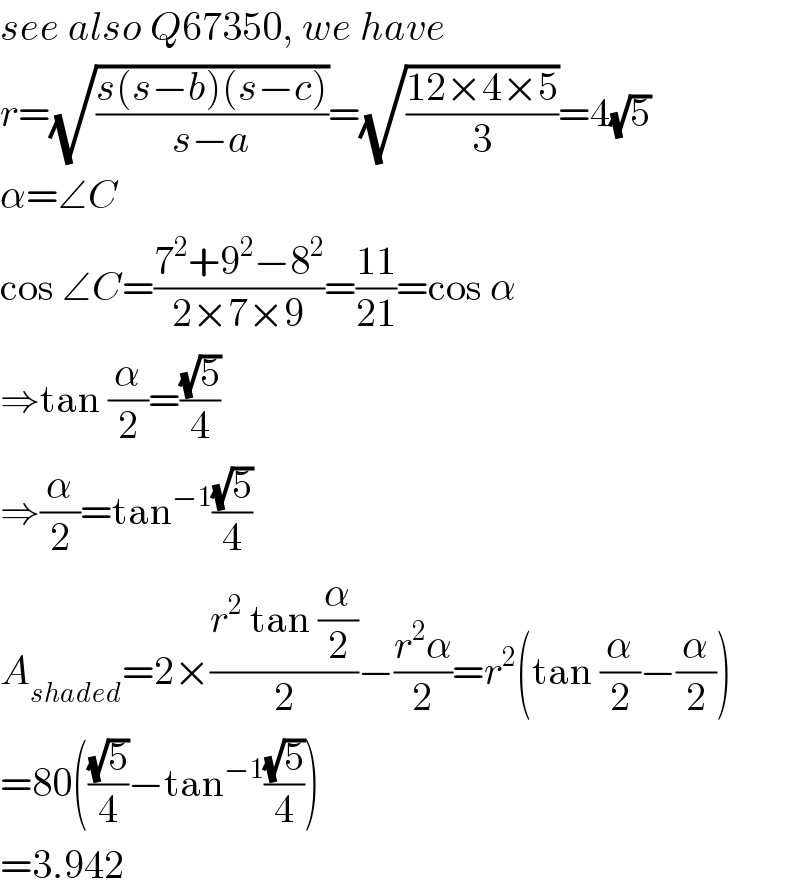
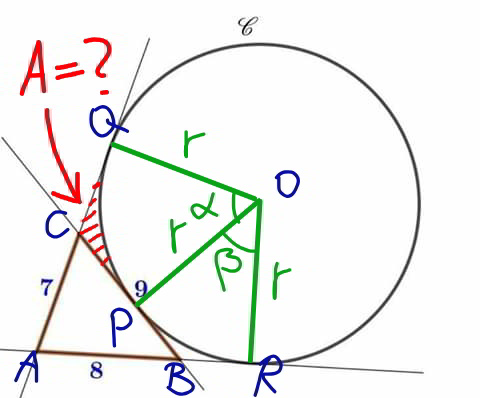
$${see}\:{also}\:{Q}\mathrm{67350},\:{we}\:{have} \\ $$$${r}=\sqrt{\frac{{s}\left({s}−{b}\right)\left({s}−{c}\right)}{{s}−{a}}}=\sqrt{\frac{\mathrm{12}×\mathrm{4}×\mathrm{5}}{\mathrm{3}}}=\mathrm{4}\sqrt{\mathrm{5}} \\ $$$$\alpha=\angle{C} \\ $$$$\mathrm{cos}\:\angle{C}=\frac{\mathrm{7}^{\mathrm{2}} +\mathrm{9}^{\mathrm{2}} −\mathrm{8}^{\mathrm{2}} }{\mathrm{2}×\mathrm{7}×\mathrm{9}}=\frac{\mathrm{11}}{\mathrm{21}}=\mathrm{cos}\:\alpha \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}=\frac{\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\Rightarrow\frac{\alpha}{\mathrm{2}}=\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$${A}_{{shaded}} =\mathrm{2}×\frac{{r}^{\mathrm{2}} \:\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}}{\mathrm{2}}−\frac{{r}^{\mathrm{2}} \alpha}{\mathrm{2}}={r}^{\mathrm{2}} \left(\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}−\frac{\alpha}{\mathrm{2}}\right) \\ $$$$=\mathrm{80}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{4}}−\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{5}}}{\mathrm{4}}\right) \\ $$$$=\mathrm{3}.\mathrm{942} \\ $$
Commented by Prithwish sen last updated on 29/Aug/19

$$\mathrm{Sir}\:\mathrm{is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{possibility}\:\mathrm{that}\:\mathrm{OA}\:\mathrm{might}\:\mathrm{be} \\ $$$$\mathrm{gone}\:\mathrm{through}\:\mathrm{P}\:? \\ $$
Commented by TawaTawa last updated on 29/Aug/19

$$\mathrm{Great}.\:\mathrm{Thanks}\:\mathrm{sir}.\: \\ $$
Commented by mr W last updated on 29/Aug/19
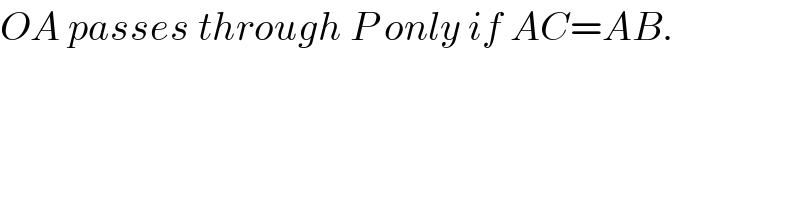
$${OA}\:{passes}\:{through}\:{P}\:{only}\:{if}\:{AC}={AB}. \\ $$
Commented by Prithwish sen last updated on 29/Aug/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
