Question Number 133173 by john_santu last updated on 19/Feb/21
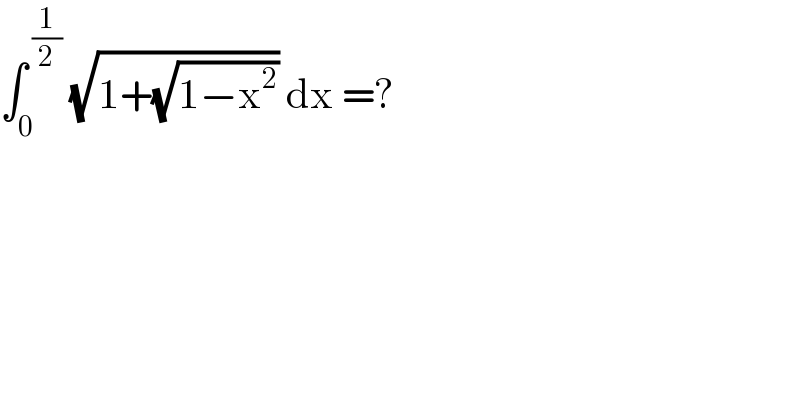
$$\int_{\mathrm{0}} ^{\:\frac{\mathrm{1}}{\mathrm{2}}} \:\sqrt{\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}\:=? \\ $$
Answered by EDWIN88 last updated on 19/Feb/21
![I=∫_0 ^( (1/2)) (√(1+(√(1−x^2 )))) dx by substitution (√(1+(√(1−x^2 )))) = (√(2−s^2 )) ⇒(√(1−x^2 )) = 1−s^2 ; x = s(√(2−s^2 )) (dx/ds) = (√(2−s^2 )) − (s^2 /( (√(2−s^2 )))) = ((2−2s^2 )/( (√(2−s^2 )))) I=∫_(0 ) ^( (((√3)−1)/2)) (2−2s^2 )ds = [(2s−(2/3)s^3 )]_0 ^(((√3)−1)/2) = ((3(√3) −1)/6) .](https://www.tinkutara.com/question/Q133175.png)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\:\frac{\mathrm{1}}{\mathrm{2}}} \sqrt{\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}\: \\ $$$$\mathrm{by}\:\mathrm{substitution}\:\sqrt{\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:=\:\sqrt{\mathrm{2}−\mathrm{s}^{\mathrm{2}} }\: \\ $$$$\Rightarrow\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:=\:\mathrm{1}−\mathrm{s}^{\mathrm{2}} \:;\:\mathrm{x}\:=\:\mathrm{s}\sqrt{\mathrm{2}−\mathrm{s}^{\mathrm{2}} } \\ $$$$\:\frac{\mathrm{dx}}{\mathrm{ds}}\:=\:\sqrt{\mathrm{2}−\mathrm{s}^{\mathrm{2}} }\:−\:\frac{\mathrm{s}^{\mathrm{2}} }{\:\sqrt{\mathrm{2}−\mathrm{s}^{\mathrm{2}} }}\:=\:\frac{\mathrm{2}−\mathrm{2s}^{\mathrm{2}} }{\:\sqrt{\mathrm{2}−\mathrm{s}^{\mathrm{2}} }} \\ $$$$\mathrm{I}=\int_{\mathrm{0}\:} ^{\:\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}} \left(\mathrm{2}−\mathrm{2s}^{\mathrm{2}} \:\right)\mathrm{ds}\:=\:\left[\left(\mathrm{2s}−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{s}^{\mathrm{3}} \right)\right]_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}} \\ $$$$=\:\frac{\mathrm{3}\sqrt{\mathrm{3}}\:−\mathrm{1}}{\mathrm{6}}\:.\: \\ $$
Answered by Dwaipayan Shikari last updated on 19/Feb/21

$$\sqrt{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:=\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{2}}}\:+\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \sqrt{\mathrm{1}+{x}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \sqrt{\mathrm{1}−{x}}\:{dx} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{6}} \\ $$
Answered by mathmax by abdo last updated on 20/Feb/21
![I=∫_0 ^(1/2) (√(1+(√(1−x^2 ))))dx we do the changement x=sint ⇒ I =∫_0 ^(π/6) (√(1+cost))cost dt =∫_0 ^(π/6) (√2)cos((t/2))cost dt =(√2)∫_0 ^(π/6) (1/2){cos(t+(t/2))+cos(t−(t/2))}dt =((√2)/2)∫_0 ^(π/6) cos(((3t)/2))dt +((√2)/2)∫_0 ^(π/6) cos((t/2))dt =((√2)/2)×(2/3)[sin(((3t)/2))]_0 ^(π/6) +((√2)/2)×2[sin((t/2))]_0 ^(π/6) =((√2)/3)×sin((3/2).(π/6)) +(√2)sin((π/(12))) =((√2)/3)sin((π/4))+(√2)sin((π/(12))) =((√2)/3).(1/( (√2))) +(√2).((√(2−(√3)))/2) =(1/3)+((√(2−(√3)))/( (√2)))=(1/3)+(√(1−((√3)/2)))](https://www.tinkutara.com/question/Q133215.png)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \sqrt{\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}=\mathrm{sint}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \sqrt{\mathrm{1}+\mathrm{cost}}\mathrm{cost}\:\mathrm{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \sqrt{\mathrm{2}}\mathrm{cos}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)\mathrm{cost}\:\mathrm{dt} \\ $$$$=\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{cos}\left(\mathrm{t}+\frac{\mathrm{t}}{\mathrm{2}}\right)+\mathrm{cos}\left(\mathrm{t}−\frac{\mathrm{t}}{\mathrm{2}}\right)\right\}\mathrm{dt} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \mathrm{cos}\left(\frac{\mathrm{3t}}{\mathrm{2}}\right)\mathrm{dt}\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \mathrm{cos}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)\mathrm{dt} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{3}}\left[\mathrm{sin}\left(\frac{\mathrm{3t}}{\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}×\mathrm{2}\left[\mathrm{sin}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}×\mathrm{sin}\left(\frac{\mathrm{3}}{\mathrm{2}}.\frac{\pi}{\mathrm{6}}\right)\:+\sqrt{\mathrm{2}}\mathrm{sin}\left(\frac{\pi}{\mathrm{12}}\right) \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\right)+\sqrt{\mathrm{2}}\mathrm{sin}\left(\frac{\pi}{\mathrm{12}}\right)\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:+\sqrt{\mathrm{2}}.\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}+\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\:\sqrt{\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{3}}+\sqrt{\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \\ $$$$ \\ $$
