Question Number 154854 by peter frank last updated on 22/Sep/21

Commented by Tawa11 last updated on 22/Sep/21

$$\mathrm{nice} \\ $$
Answered by mr W last updated on 22/Sep/21
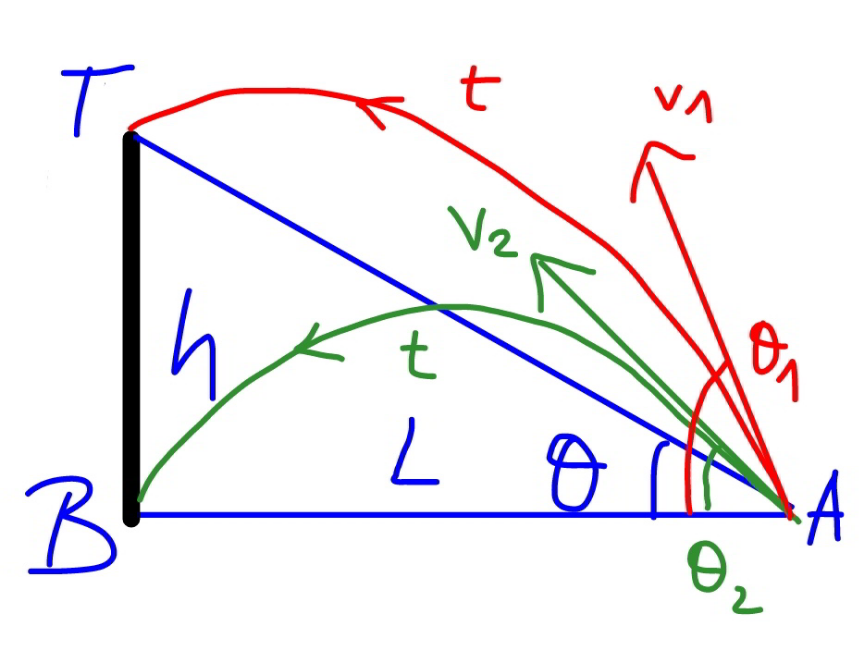
Commented by mr W last updated on 22/Sep/21
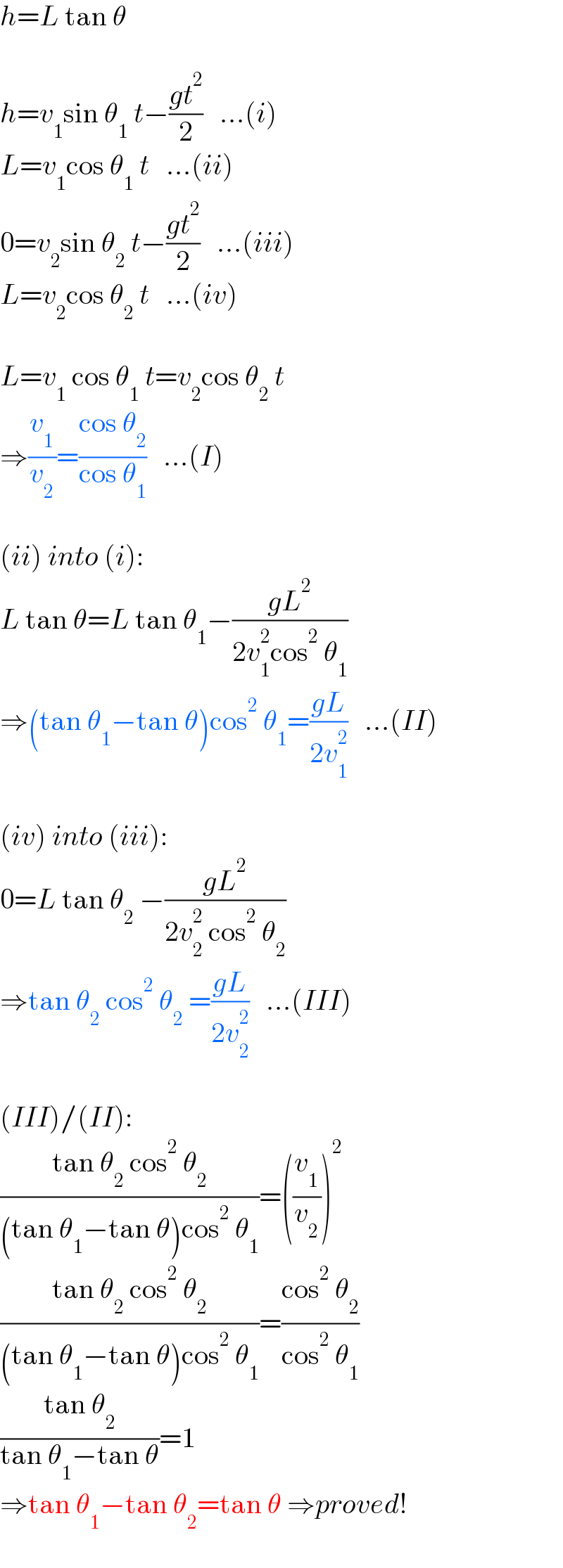
$${h}={L}\:\mathrm{tan}\:\theta \\ $$$$ \\ $$$${h}={v}_{\mathrm{1}} \mathrm{sin}\:\theta_{\mathrm{1}} \:{t}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}}\:\:\:…\left({i}\right) \\ $$$${L}={v}_{\mathrm{1}} \mathrm{cos}\:\theta_{\mathrm{1}} \:{t}\:\:\:…\left({ii}\right) \\ $$$$\mathrm{0}={v}_{\mathrm{2}} \mathrm{sin}\:\theta_{\mathrm{2}} \:{t}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}}\:\:\:…\left({iii}\right) \\ $$$${L}={v}_{\mathrm{2}} \mathrm{cos}\:\theta_{\mathrm{2}} \:{t}\:\:\:…\left({iv}\right) \\ $$$$ \\ $$$${L}={v}_{\mathrm{1}} \:\mathrm{cos}\:\theta_{\mathrm{1}} \:{t}={v}_{\mathrm{2}} \mathrm{cos}\:\theta_{\mathrm{2}} \:{t} \\ $$$$\Rightarrow\frac{{v}_{\mathrm{1}} }{{v}_{\mathrm{2}} }=\frac{\mathrm{cos}\:\theta_{\mathrm{2}} }{\mathrm{cos}\:\theta_{\mathrm{1}} }\:\:\:…\left({I}\right) \\ $$$$ \\ $$$$\left({ii}\right)\:{into}\:\left({i}\right): \\ $$$${L}\:\mathrm{tan}\:\theta={L}\:\mathrm{tan}\:\theta_{\mathrm{1}} −\frac{{gL}^{\mathrm{2}} }{\mathrm{2}{v}_{\mathrm{1}} ^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta_{\mathrm{1}} } \\ $$$$\Rightarrow\left(\mathrm{tan}\:\theta_{\mathrm{1}} −\mathrm{tan}\:\theta\right)\mathrm{cos}^{\mathrm{2}} \:\theta_{\mathrm{1}} =\frac{{gL}}{\mathrm{2}{v}_{\mathrm{1}} ^{\mathrm{2}} }\:\:\:…\left({II}\right) \\ $$$$ \\ $$$$\left({iv}\right)\:{into}\:\left({iii}\right): \\ $$$$\mathrm{0}={L}\:\mathrm{tan}\:\theta_{\mathrm{2}} \:−\frac{{gL}^{\mathrm{2}} }{\mathrm{2}{v}_{\mathrm{2}} ^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta_{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{tan}\:\theta_{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta_{\mathrm{2}} \:=\frac{{gL}}{\mathrm{2}{v}_{\mathrm{2}} ^{\mathrm{2}} }\:\:\:…\left({III}\right) \\ $$$$ \\ $$$$\left({III}\right)/\left({II}\right): \\ $$$$\frac{\mathrm{tan}\:\theta_{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta_{\mathrm{2}} }{\left(\mathrm{tan}\:\theta_{\mathrm{1}} −\mathrm{tan}\:\theta\right)\mathrm{cos}^{\mathrm{2}} \:\theta_{\mathrm{1}} }=\left(\frac{{v}_{\mathrm{1}} }{{v}_{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{tan}\:\theta_{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta_{\mathrm{2}} }{\left(\mathrm{tan}\:\theta_{\mathrm{1}} −\mathrm{tan}\:\theta\right)\mathrm{cos}^{\mathrm{2}} \:\theta_{\mathrm{1}} }=\frac{\mathrm{cos}^{\mathrm{2}} \:\theta_{\mathrm{2}} }{\mathrm{cos}^{\mathrm{2}} \:\theta_{\mathrm{1}} } \\ $$$$\frac{\mathrm{tan}\:\theta_{\mathrm{2}} }{\mathrm{tan}\:\theta_{\mathrm{1}} −\mathrm{tan}\:\theta}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{tan}\:\theta_{\mathrm{1}} −\mathrm{tan}\:\theta_{\mathrm{2}} =\mathrm{tan}\:\theta\:\Rightarrow{proved}! \\ $$
Commented by peter frank last updated on 22/Sep/21
$$\mathrm{appriciate}\:\mathrm{sir}.\mathrm{thank}\:\mathrm{you} \\ $$
Commented by peter frank last updated on 22/Sep/21
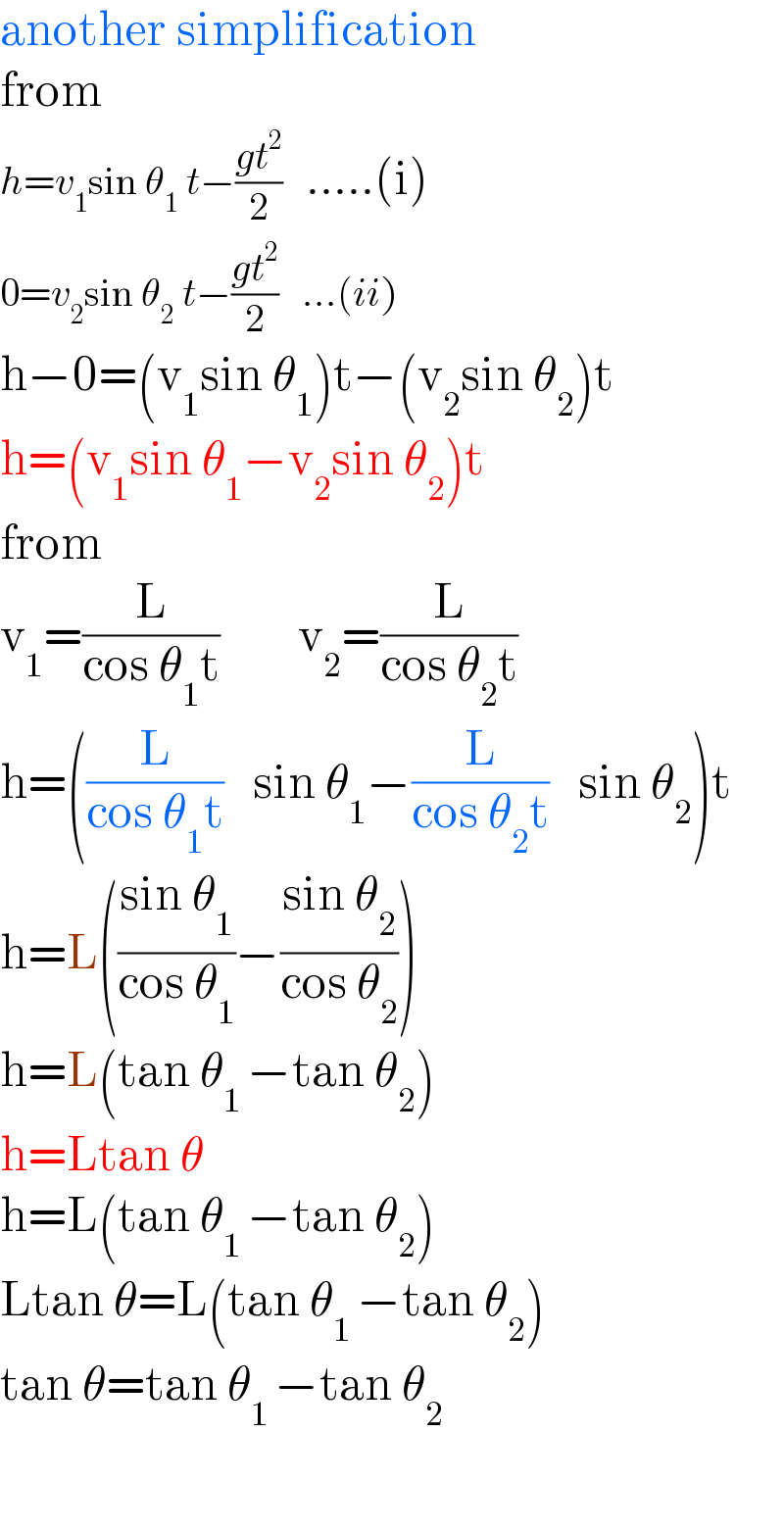
$$\mathrm{another}\:\mathrm{simplification} \\ $$$$\mathrm{from}\: \\ $$$${h}={v}_{\mathrm{1}} \mathrm{sin}\:\theta_{\mathrm{1}} \:{t}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}}\:\:\:…..\left(\mathrm{i}\right) \\ $$$$\mathrm{0}={v}_{\mathrm{2}} \mathrm{sin}\:\theta_{\mathrm{2}} \:{t}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}}\:\:\:…\left({ii}\right) \\ $$$$\mathrm{h}−\mathrm{0}=\left(\mathrm{v}_{\mathrm{1}} \mathrm{sin}\:\theta_{\mathrm{1}} \right)\mathrm{t}−\left(\mathrm{v}_{\mathrm{2}} \mathrm{sin}\:\theta_{\mathrm{2}} \right)\mathrm{t}\: \\ $$$$\mathrm{h}=\left(\mathrm{v}_{\mathrm{1}} \mathrm{sin}\:\theta_{\mathrm{1}} −\mathrm{v}_{\mathrm{2}} \mathrm{sin}\:\theta_{\mathrm{2}} \right)\mathrm{t} \\ $$$$\mathrm{from}\: \\ $$$$\mathrm{v}_{\mathrm{1}} =\frac{\mathrm{L}}{\mathrm{cos}\:\theta_{\mathrm{1}} \mathrm{t}}\:\:\:\:\:\:\:\:\mathrm{v}_{\mathrm{2}} =\frac{\mathrm{L}}{\mathrm{cos}\:\theta_{\mathrm{2}} \mathrm{t}} \\ $$$$\mathrm{h}=\left(\frac{\mathrm{L}}{\mathrm{cos}\:\theta_{\mathrm{1}} \mathrm{t}}\:\:\:\mathrm{sin}\:\theta_{\mathrm{1}} −\frac{\mathrm{L}}{\mathrm{cos}\:\theta_{\mathrm{2}} \mathrm{t}}\:\:\:\mathrm{sin}\:\theta_{\mathrm{2}} \right)\mathrm{t} \\ $$$$\mathrm{h}=\mathrm{L}\left(\frac{\mathrm{sin}\:\theta_{\mathrm{1}} }{\mathrm{cos}\:\theta_{\mathrm{1}} }−\frac{\mathrm{sin}\:\theta_{\mathrm{2}} }{\mathrm{cos}\:\theta_{\mathrm{2}} }\right) \\ $$$$\mathrm{h}=\mathrm{L}\left(\mathrm{tan}\:\theta_{\mathrm{1}\:} −\mathrm{tan}\:\theta_{\mathrm{2}} \right) \\ $$$$\mathrm{h}=\mathrm{Ltan}\:\theta \\ $$$$\mathrm{h}=\mathrm{L}\left(\mathrm{tan}\:\theta_{\mathrm{1}\:} −\mathrm{tan}\:\theta_{\mathrm{2}} \right) \\ $$$$\mathrm{Ltan}\:\theta=\mathrm{L}\left(\mathrm{tan}\:\theta_{\mathrm{1}\:} −\mathrm{tan}\:\theta_{\mathrm{2}} \right) \\ $$$$\mathrm{tan}\:\theta=\mathrm{tan}\:\theta_{\mathrm{1}\:} −\mathrm{tan}\:\theta_{\mathrm{2}} \\ $$$$ \\ $$
Commented by mr W last updated on 23/Sep/21
������
