Question Number 89322 by I want to learn more last updated on 16/Apr/20
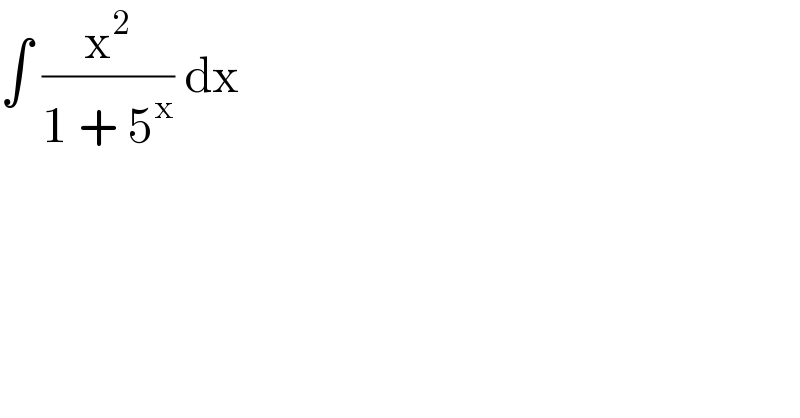
$$\int\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{1}\:+\:\mathrm{5}^{\mathrm{x}} }\:\mathrm{dx} \\ $$
Commented by mathmax by abdo last updated on 17/Apr/20
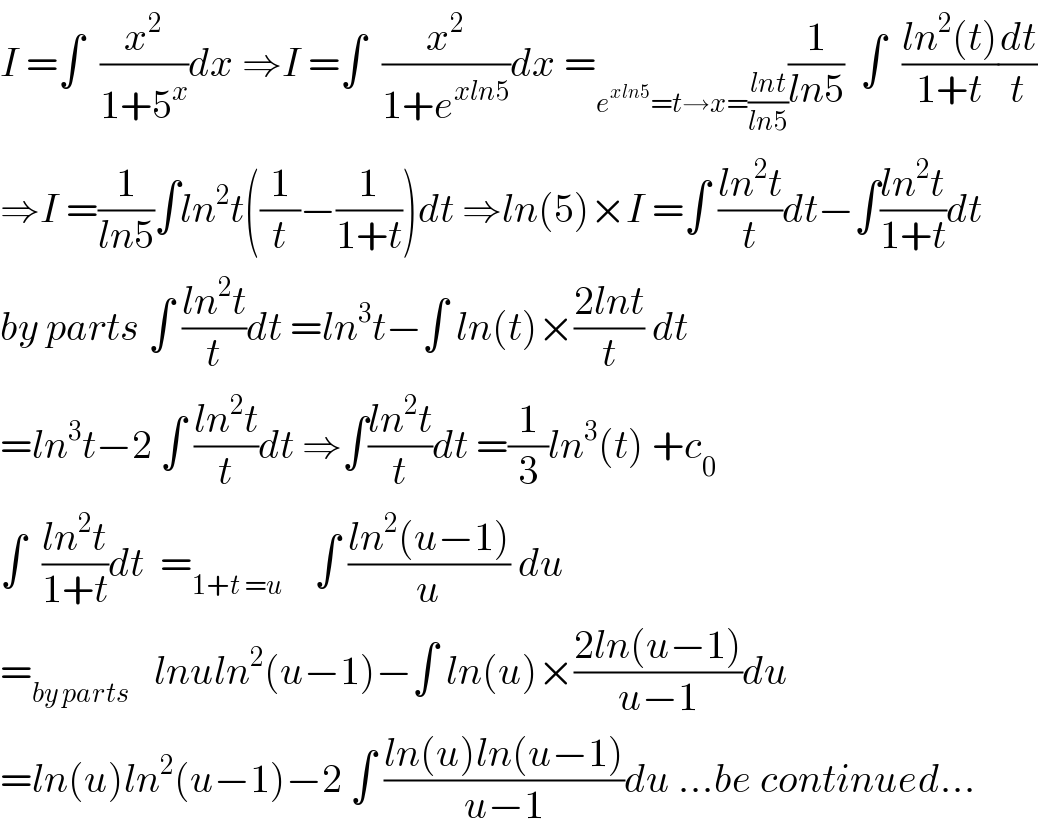
$${I}\:=\int\:\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{5}^{{x}} }{dx}\:\Rightarrow{I}\:=\int\:\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{e}^{{xln}\mathrm{5}} }{dx}\:=_{{e}^{{xln}\mathrm{5}} ={t}\rightarrow{x}=\frac{{lnt}}{{ln}\mathrm{5}}} \frac{\mathrm{1}}{{ln}\mathrm{5}}\:\:\int\:\:\frac{{ln}^{\mathrm{2}} \left({t}\right)}{\mathrm{1}+{t}}\frac{{dt}}{{t}} \\ $$$$\Rightarrow{I}\:=\frac{\mathrm{1}}{{ln}\mathrm{5}}\int{ln}^{\mathrm{2}} {t}\left(\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}}{\mathrm{1}+{t}}\right){dt}\:\Rightarrow{ln}\left(\mathrm{5}\right)×{I}\:=\int\:\frac{{ln}^{\mathrm{2}} {t}}{{t}}{dt}−\int\frac{{ln}^{\mathrm{2}} {t}}{\mathrm{1}+{t}}{dt} \\ $$$${by}\:{parts}\:\int\:\frac{{ln}^{\mathrm{2}} {t}}{{t}}{dt}\:={ln}^{\mathrm{3}} {t}−\int\:{ln}\left({t}\right)×\frac{\mathrm{2}{lnt}}{{t}}\:{dt} \\ $$$$={ln}^{\mathrm{3}} {t}−\mathrm{2}\:\int\:\frac{{ln}^{\mathrm{2}} {t}}{{t}}{dt}\:\Rightarrow\int\frac{{ln}^{\mathrm{2}} {t}}{{t}}{dt}\:=\frac{\mathrm{1}}{\mathrm{3}}{ln}^{\mathrm{3}} \left({t}\right)\:+{c}_{\mathrm{0}} \\ $$$$\int\:\:\frac{{ln}^{\mathrm{2}} {t}}{\mathrm{1}+{t}}{dt}\:\:=_{\mathrm{1}+{t}\:={u}} \:\:\:\:\int\:\frac{{ln}^{\mathrm{2}} \left({u}−\mathrm{1}\right)}{{u}}\:{du} \\ $$$$=_{{by}\:{parts}} \:\:\:{lnuln}^{\mathrm{2}} \left({u}−\mathrm{1}\right)−\int\:{ln}\left({u}\right)×\frac{\mathrm{2}{ln}\left({u}−\mathrm{1}\right)}{{u}−\mathrm{1}}{du} \\ $$$$={ln}\left({u}\right){ln}^{\mathrm{2}} \left({u}−\mathrm{1}\right)−\mathrm{2}\:\int\:\frac{{ln}\left({u}\right){ln}\left({u}−\mathrm{1}\right)}{{u}−\mathrm{1}}{du}\:…{be}\:{continued}… \\ $$
Commented by I want to learn more last updated on 17/Apr/20

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{waiting} \\ $$
