Question-155421

Question Number 155421 by SANOGO last updated on 30/Sep/21

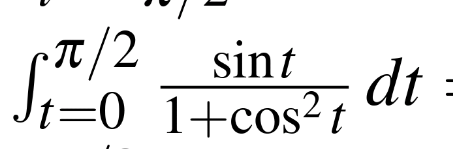
Answered by puissant last updated on 30/Sep/21

Q=∫_0 ^(π/2) ((sint)/(1+cos^2 t))dt = −∫_0 ^(π/2) ((−sint)/(1+cos^2 t))dt =−[arctan(cost)]_0 ^(π/2) = −(0−arctan(1)) ∴∵ Q = (π/4)..

$${Q}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sint}}{\mathrm{1}+{cos}^{\mathrm{2}} {t}}{dt}\:=\:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{−{sint}}{\mathrm{1}+{cos}^{\mathrm{2}} {t}}{dt} \\ $$$$=−\left[{arctan}\left({cost}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\:−\left(\mathrm{0}−{arctan}\left(\mathrm{1}\right)\right) \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\therefore\because\:\:{Q}\:=\:\frac{\pi}{\mathrm{4}}.. \\ $$

Commented by SANOGO last updated on 30/Sep/21

$${merci}\:{bien} \\ $$

Answered by ArielVyny last updated on 30/Sep/21

u=tan((t/2))→du=(1/2)(1+u^2 )dt→dt=(2/(1+u^2 ))du ∫_0 ^1 (((2u)/(1+u^2 ))/(1+(((1−u^2 )/(1+u^2 )))^2 )).(2/(1+u^2 ))du=∫_0 ^1 ((2u)/(1+u^2 )).(2/((1+u^2 )+(((1−u^2 )^2 )/(1+u^2 ))))du ∫_0 ^1 ((4u)/((1+u^2 )^2 +(1−u^2 )^2 ))du=4∫_0 ^1 (u/(u^4 +2u^2 +1+u^4 −2u^2 +1)) 4∫_0 ^1 (u/(2u^4 +2))du=2∫_0 ^1 (u/(u^4 +1))du u^2 =x→2udu=dx ∫_0 ^1 (dx/(x^2 +1))=∫_0 ^(π/2) ((sint)/(1+cos^2 t))dt=(π/4)

$${u}={tan}\left(\frac{{t}}{\mathrm{2}}\right)\rightarrow{du}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{u}^{\mathrm{2}} \right){dt}\rightarrow{dt}=\frac{\mathrm{2}}{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}{\mathrm{1}+\left(\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }\right)^{\mathrm{2}} }.\frac{\mathrm{2}}{\mathrm{1}+{u}^{\mathrm{2}} }{du}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }.\frac{\mathrm{2}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)+\frac{\left(\mathrm{1}−{u}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }}{du} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{4}{u}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{1}−{u}^{\mathrm{2}} \right)^{\mathrm{2}} }{du}=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}}{{u}^{\mathrm{4}} +\mathrm{2}{u}^{\mathrm{2}} +\mathrm{1}+{u}^{\mathrm{4}} −\mathrm{2}{u}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}}{\mathrm{2}{u}^{\mathrm{4}} +\mathrm{2}}{du}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}}{{u}^{\mathrm{4}} +\mathrm{1}}{du} \\ $$$${u}^{\mathrm{2}} ={x}\rightarrow\mathrm{2}{udu}={dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sint}}{\mathrm{1}+{cos}^{\mathrm{2}} {t}}{dt}=\frac{\pi}{\mathrm{4}} \\ $$

Commented by SANOGO last updated on 30/Sep/21

$${merci}\:{bien} \\ $$

Answered by physicstutes last updated on 30/Sep/21

let x = cos t ⇒ dx = −sin t dt determinant ((t,0,(π/2)),(x,1,0)) ∫_0 ^(π/2) ((sin t)/(1+cos^2 t))dt = ∫_1 ^0 ((sin t)/(1+x^2 ))(−(dx/(sin t)))= ∫_0 ^1 (dx/(1+x^2 )) = tan^(−1) (x)]_0 ^1 =(π/4)

$$\mathrm{let}\:{x}\:=\:\mathrm{cos}\:{t}\:\Rightarrow\:{dx}\:=\:−\mathrm{sin}\:{t}\:{dt} \\ $$$$\begin{array}{|c|c|}{{t}}&\hline{\mathrm{0}}&\hline{\frac{\pi}{\mathrm{2}}}\\{{x}}&\hline{\mathrm{1}}&\hline{\mathrm{0}}\\\hline\end{array} \\ $$$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{\mathrm{sin}\:{t}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} {t}}{dt}\:=\:\underset{\mathrm{1}} {\overset{\mathrm{0}} {\int}}\frac{\mathrm{sin}\:{t}}{\mathrm{1}+{x}^{\mathrm{2}} }\left(−\frac{{dx}}{\mathrm{sin}\:{t}}\right)=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\left.=\:\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\pi}{\mathrm{4}} \\ $$

Commented by SANOGO last updated on 30/Sep/21

$${merci}\:{bien} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply