Question Number 89938 by jagoll last updated on 20/Apr/20
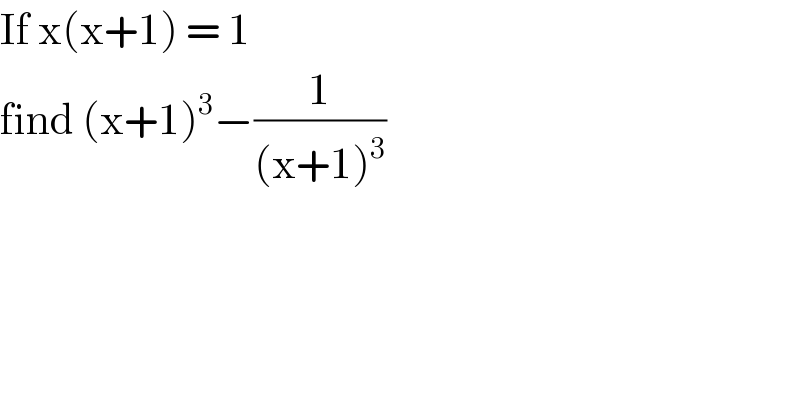
$$\mathrm{If}\:\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)\:=\:\mathrm{1}\: \\ $$$$\mathrm{find}\:\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} −\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$
Commented by john santu last updated on 20/Apr/20
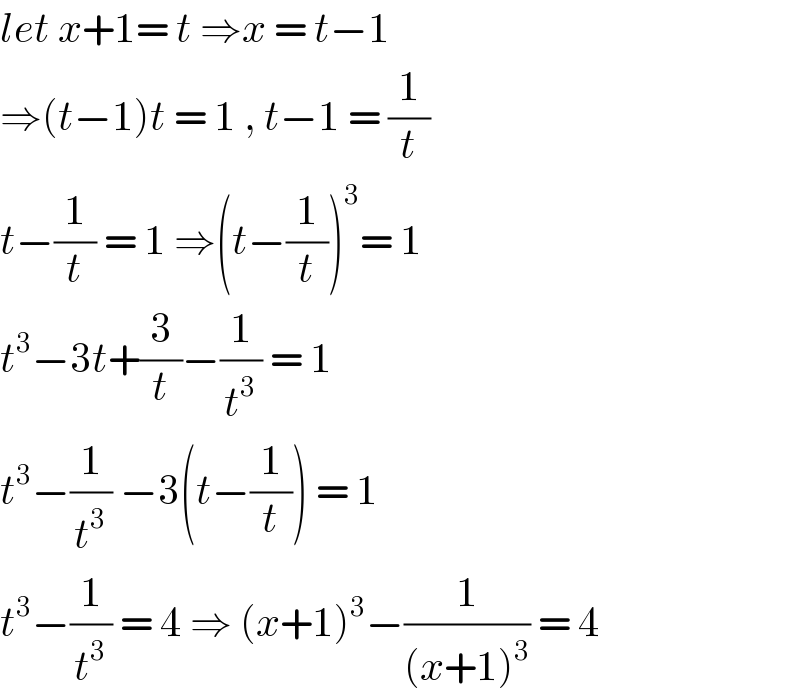
$${let}\:{x}+\mathrm{1}=\:{t}\:\Rightarrow{x}\:=\:{t}−\mathrm{1} \\ $$$$\Rightarrow\left({t}−\mathrm{1}\right){t}\:=\:\mathrm{1}\:,\:{t}−\mathrm{1}\:=\:\frac{\mathrm{1}}{{t}} \\ $$$${t}−\frac{\mathrm{1}}{{t}}\:=\:\mathrm{1}\:\Rightarrow\left({t}−\frac{\mathrm{1}}{{t}}\right)^{\mathrm{3}} =\:\mathrm{1}\: \\ $$$${t}^{\mathrm{3}} −\mathrm{3}{t}+\frac{\mathrm{3}}{{t}}−\frac{\mathrm{1}}{{t}^{\mathrm{3}} }\:=\:\mathrm{1}\: \\ $$$${t}^{\mathrm{3}} −\frac{\mathrm{1}}{{t}^{\mathrm{3}} }\:−\mathrm{3}\left({t}−\frac{\mathrm{1}}{{t}}\right)\:=\:\mathrm{1} \\ $$$${t}^{\mathrm{3}} −\frac{\mathrm{1}}{{t}^{\mathrm{3}} }\:=\:\mathrm{4}\:\Rightarrow\:\left({x}+\mathrm{1}\right)^{\mathrm{3}} −\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} }\:=\:\mathrm{4}\: \\ $$
