Solve-for-x-10-4-x-x-4-10-8-

Question Number 24443 by Tinkutara last updated on 18/Nov/17

$${Solve}\:{for}\:{x}: \\ $$$$\left(\mathrm{10}^{−\mathrm{4}} {x}\right)^{{x}} =\mathrm{4}×\mathrm{10}^{−\mathrm{8}} \\ $$

Answered by ajfour last updated on 18/Nov/17

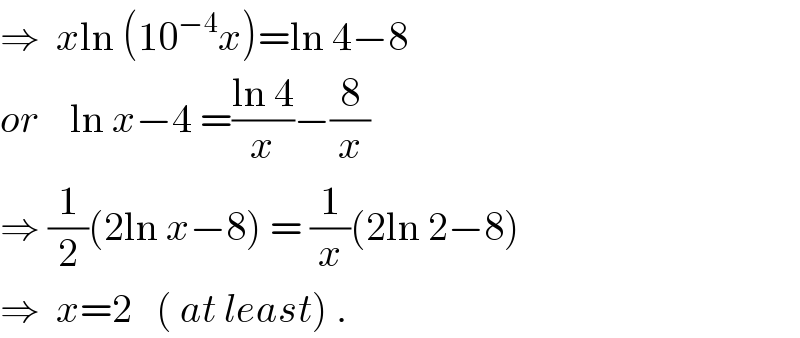
⇒ xln (10^(−4) x)=ln 4−8 or ln x−4 =((ln 4)/x)−(8/x) ⇒ (1/2)(2ln x−8) = (1/x)(2ln 2−8) ⇒ x=2 ( at least) .

$$\Rightarrow\:\:{x}\mathrm{ln}\:\left(\mathrm{10}^{−\mathrm{4}} {x}\right)=\mathrm{ln}\:\mathrm{4}−\mathrm{8} \\ $$$${or}\:\:\:\:\mathrm{ln}\:{x}−\mathrm{4}\:=\frac{\mathrm{ln}\:\mathrm{4}}{{x}}−\frac{\mathrm{8}}{{x}} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2ln}\:{x}−\mathrm{8}\right)\:=\:\frac{\mathrm{1}}{{x}}\left(\mathrm{2ln}\:\mathrm{2}−\mathrm{8}\right) \\ $$$$\Rightarrow\:\:{x}=\mathrm{2}\:\:\:\left(\:{at}\:{least}\right)\:. \\ $$

Commented by Tinkutara last updated on 19/Nov/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Answered by mrW1 last updated on 19/Nov/17

To simply the writing, let′s say the equation is (ax)^x =b. [ln (ax)]x=ln b [ln (ax)](ax)=aln b [ln (ax)]e^(ln (ax)) =aln b ⇒ln (ax)=W(aln b) ⇒ax=e^(W(aln b)) =((aln b)/(W(aln b))) ⇒x=((ln b)/(W(aln b))) with a=10^(−4) and b=4×10^(−8) ⇒x=((ln 4−8ln 10)/(W[10^(−4) (ln 4−8ln 10)])) =((−17.0344)/(W[−1.70344×10^(−3) ]))= { ((((−17.0344)/(−8.5172))=2)),((((−17.0344)/(−0.0017064))=9983)) :} i.e. there are two solutions: x=2 and 9983.

$${To}\:{simply}\:{the}\:{writing},\:{let}'{s}\:{say} \\ $$$${the}\:{equation}\:{is}\:\left({ax}\right)^{{x}} ={b}. \\ $$$$\left[\mathrm{ln}\:\left({ax}\right)\right]{x}=\mathrm{ln}\:{b} \\ $$$$\left[\mathrm{ln}\:\left({ax}\right)\right]\left({ax}\right)={a}\mathrm{ln}\:{b} \\ $$$$\left[\mathrm{ln}\:\left({ax}\right)\right]{e}^{\mathrm{ln}\:\left({ax}\right)} ={a}\mathrm{ln}\:{b} \\ $$$$\Rightarrow\mathrm{ln}\:\left({ax}\right)=\mathbb{W}\left({a}\mathrm{ln}\:{b}\right) \\ $$$$\Rightarrow{ax}={e}^{\mathbb{W}\left({a}\mathrm{ln}\:{b}\right)} =\frac{{a}\mathrm{ln}\:{b}}{\mathbb{W}\left({a}\mathrm{ln}\:{b}\right)} \\ $$$$\Rightarrow{x}=\frac{\mathrm{ln}\:{b}}{\mathbb{W}\left({a}\mathrm{ln}\:{b}\right)} \\ $$$$ \\ $$$${with}\:{a}=\mathrm{10}^{−\mathrm{4}} \:{and}\:{b}=\mathrm{4}×\mathrm{10}^{−\mathrm{8}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{ln}\:\mathrm{4}−\mathrm{8ln}\:\mathrm{10}}{{W}\left[\mathrm{10}^{−\mathrm{4}} \left(\mathrm{ln}\:\mathrm{4}−\mathrm{8ln}\:\mathrm{10}\right)\right]} \\ $$$$=\frac{−\mathrm{17}.\mathrm{0344}}{{W}\left[−\mathrm{1}.\mathrm{70344}×\mathrm{10}^{−\mathrm{3}} \right]}=\begin{cases}{\frac{−\mathrm{17}.\mathrm{0344}}{−\mathrm{8}.\mathrm{5172}}=\mathrm{2}}\\{\frac{−\mathrm{17}.\mathrm{0344}}{−\mathrm{0}.\mathrm{0017064}}=\mathrm{9983}}\end{cases} \\ $$$${i}.{e}.\:{there}\:{are}\:{two}\:{solutions}: \\ $$$${x}=\mathrm{2}\:{and}\:\mathrm{9983}. \\ $$

Commented by Tinkutara last updated on 19/Nov/17

And how to find W[−1.703×10^(−5) ] using Geogebra?

$${And}\:{how}\:{to}\:{find}\:{W}\left[−\mathrm{1}.\mathrm{703}×\mathrm{10}^{−\mathrm{5}} \right] \\ $$$${using}\:{Geogebra}? \\ $$

Commented by mrW1 last updated on 19/Nov/17

If you don′t have a calculator for W−function, you can calculate the value(s) of W(p) using Geogebra. The value(s) of W(p) is (are) the root(s) of equation f(x)=xe^x −p=0 For p<0 there are usually two roots.

$${If}\:{you}\:{don}'{t}\:{have}\:{a}\:{calculator}\:{for} \\ $$$${W}−{function},\:{you}\:{can}\:{calculate}\:{the} \\ $$$${value}\left({s}\right)\:{of}\:{W}\left({p}\right)\:{using}\:{Geogebra}. \\ $$$${The}\:{value}\left({s}\right)\:{of}\:{W}\left({p}\right)\:{is}\:\left({are}\right)\:{the} \\ $$$${root}\left({s}\right)\:{of}\:{equation} \\ $$$${f}\left({x}\right)={xe}^{{x}} −{p}=\mathrm{0} \\ $$$${For}\:{p}<\mathrm{0}\:{there}\:{are}\:{usually}\:{two}\:{roots}. \\ $$

Commented by mrW1 last updated on 19/Nov/17