Question Number 24526 by ajfour last updated on 20/Nov/17
Commented by ajfour last updated on 20/Nov/17

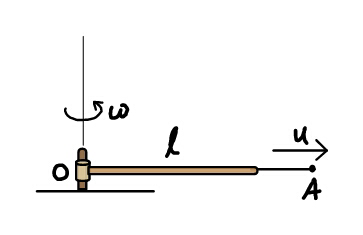
$${A}\:{thin}\:{rod}\:{rotates}\:{in}\:{horizontal} \\ $$$${plane}\:{with}\:{a}\:{constant}\:{angular}\: \\ $$$${velocity}\:\boldsymbol{\omega}.{From}\:{its}\:{farther}\:{end} \\ $$$${a}\:{needle}\:{emerges}\:{at}\:{a}\:{constant} \\ $$$${relative}\:{velocity}\:\boldsymbol{{u}}\:{along}\:{the}\:{rod}. \\ $$$${Find}\:{the}\:{initial}\:{absolute}\: \\ $$$${acceleration}\:{of}\:{the}\:{tip}\:{of}\:{the}\: \\ $$$${needle}\:{taking}\:{O}\:{to}\:{be}\:{the}\:{origin}. \\ $$
Answered by ajfour last updated on 20/Nov/17
Answered by sma3l2996 last updated on 20/Nov/17
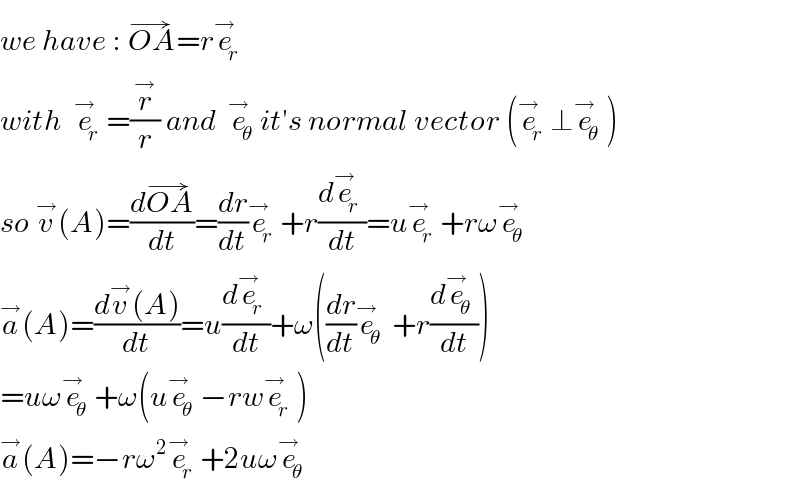
$${we}\:{have}\::\:\overset{\rightarrow} {{OA}}={r}\overset{\rightarrow} {{e}}_{{r}} \: \\ $$$${with}\:\:\overset{\rightarrow} {{e}}_{{r}} =\frac{\overset{\rightarrow} {{r}}}{{r}}\:{and}\:\:\overset{\rightarrow} {{e}}_{\theta} {it}'{s}\:{normal}\:{vector}\:\left(\overset{\rightarrow} {{e}}_{{r}} \bot\overset{\rightarrow} {{e}}_{\theta} \right) \\ $$$${so}\:\overset{\rightarrow} {{v}}\left({A}\right)=\frac{{d}\overset{\rightarrow} {{OA}}}{{dt}}=\frac{{dr}}{{dt}}\overset{\rightarrow} {{e}}_{{r}} +{r}\frac{{d}\overset{\rightarrow} {{e}}_{{r}} }{{dt}}={u}\overset{\rightarrow} {{e}}_{{r}} +{r}\omega\overset{\rightarrow} {{e}}_{\theta} \\ $$$$\overset{\rightarrow} {{a}}\left({A}\right)=\frac{{d}\overset{\rightarrow} {{v}}\left({A}\right)}{{dt}}={u}\frac{{d}\overset{\rightarrow} {{e}}_{{r}} }{{dt}}+\omega\left(\frac{{dr}}{{dt}}\overset{\rightarrow} {{e}}_{\theta\:} +{r}\frac{{d}\overset{\rightarrow} {{e}}_{\theta} }{{dt}}\right) \\ $$$$={u}\omega\overset{\rightarrow} {{e}}_{\theta} +\omega\left({u}\overset{\rightarrow} {{e}}_{\theta} −{rw}\overset{\rightarrow} {{e}}_{{r}} \right) \\ $$$$\overset{\rightarrow} {{a}}\left({A}\right)=−{r}\omega^{\mathrm{2}} \overset{\rightarrow} {{e}}_{{r}} +\mathrm{2}{u}\omega\overset{\rightarrow} {{e}}_{\theta} \\ $$
Commented by ajfour last updated on 20/Nov/17

$${Thanks}. \\ $$
