Question Number 90113 by M±th+et£s last updated on 21/Apr/20
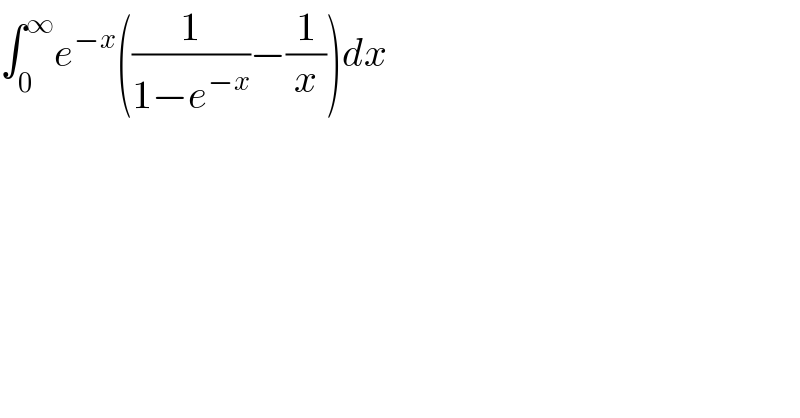
$$\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} \left(\frac{\mathrm{1}}{\mathrm{1}−{e}^{−{x}} }−\frac{\mathrm{1}}{{x}}\right){dx} \\ $$
Answered by maths mind last updated on 21/Apr/20
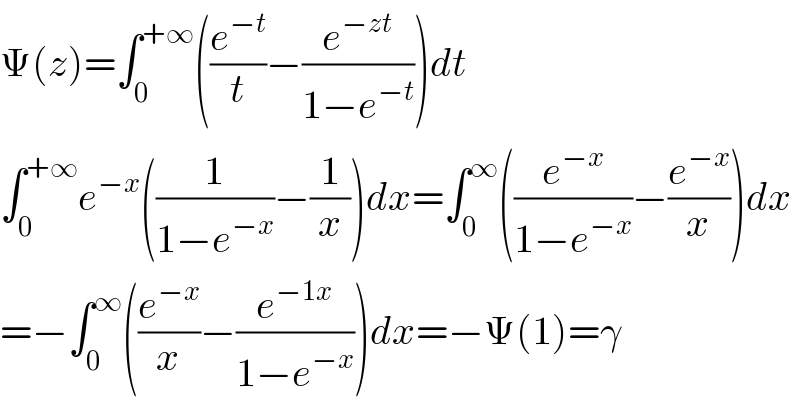
$$\Psi\left({z}\right)=\int_{\mathrm{0}} ^{+\infty} \left(\frac{{e}^{−{t}} }{{t}}−\frac{{e}^{−{zt}} }{\mathrm{1}−{e}^{−{t}} }\right){dt} \\ $$$$\int_{\mathrm{0}} ^{+\infty} {e}^{−{x}} \left(\frac{\mathrm{1}}{\mathrm{1}−{e}^{−{x}} }−\frac{\mathrm{1}}{{x}}\right){dx}=\int_{\mathrm{0}} ^{\infty} \left(\frac{{e}^{−{x}} }{\mathrm{1}−{e}^{−{x}} }−\frac{{e}^{−{x}} }{{x}}\right){dx} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \left(\frac{{e}^{−{x}} }{{x}}−\frac{{e}^{−\mathrm{1}{x}} }{\mathrm{1}−{e}^{−{x}} }\right){dx}=−\Psi\left(\mathrm{1}\right)=\gamma \\ $$
Commented by M±th+et£s last updated on 21/Apr/20
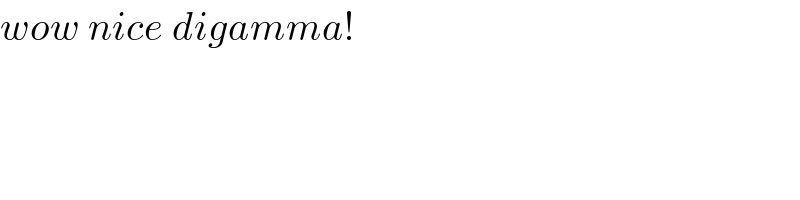
$${wow}\:{nice}\:{digamma}! \\ $$
Commented by maths mind last updated on 21/Apr/20

$${thanx}\:{sir} \\ $$$$ \\ $$
