Menu Close

I-n-t-0-dt-t-1-t-2-t-n-

Tinku Tara 0 Comments
Pin




Question Number 90135 by Ar Brandon last updated on 21/Apr/20
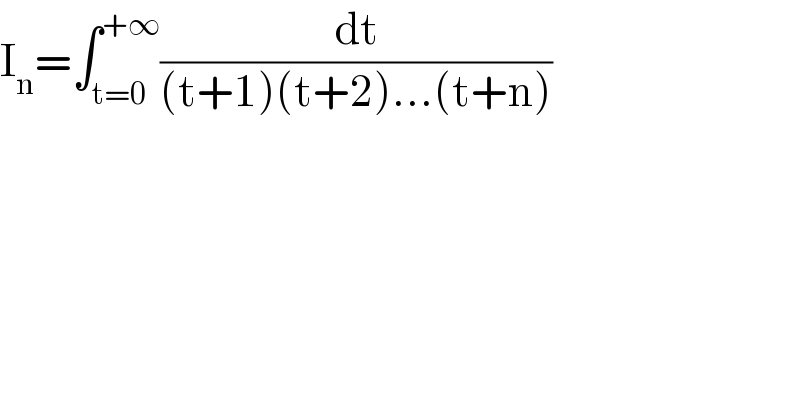
I_n =∫_(t=0) ^(+∞) (dt/((t+1)(t+2)...(t+n)))
$$\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{t}=\mathrm{0}} ^{+\infty} \frac{\mathrm{dt}}{\left(\mathrm{t}+\mathrm{1}\right)\left(\mathrm{t}+\mathrm{2}\right)…\left(\mathrm{t}+\mathrm{n}\right)} \\ $$
Answered by TANMAY PANACEA. last updated on 21/Apr/20
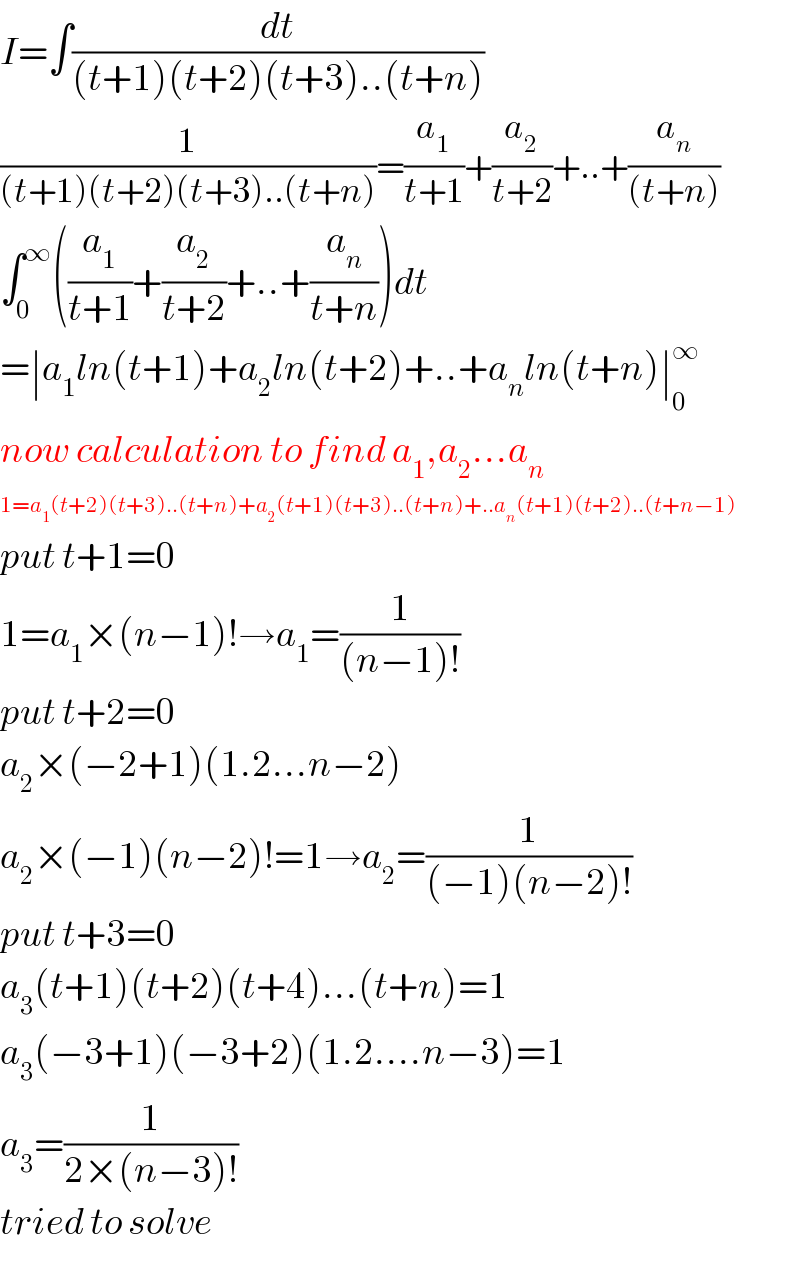
I=∫(dt/((t+1)(t+2)(t+3)..(t+n))) (1/((t+1)(t+2)(t+3)..(t+n)))=(a_1 /(t+1))+(a_2 /(t+2))+..+(a_n /((t+n))) ∫_0 ^∞ ((a_1 /(t+1))+(a_2 /(t+2))+..+(a_n /(t+n)))dt =∣a_1 ln(t+1)+a_2 ln(t+2)+..+a_n ln(t+n)∣_0 ^∞ now calculation to find a_1 ,a_2 ...a_n 1=a_1 (t+2)(t+3)..(t+n)+a_2 (t+1)(t+3)..(t+n)+..a_n (t+1)(t+2)..(t+n−1) put t+1=0 1=a_1 ×(n−1)!→a_1 =(1/((n−1)!)) put t+2=0 a_2 ×(−2+1)(1.2...n−2) a_2 ×(−1)(n−2)!=1→a_2 =(1/((−1)(n−2)!)) put t+3=0 a_3 (t+1)(t+2)(t+4)...(t+n)=1 a_3 (−3+1)(−3+2)(1.2....n−3)=1 a_3 =(1/(2×(n−3)!)) tried to solve
$${I}=\int\frac{{dt}}{\left({t}+\mathrm{1}\right)\left({t}+\mathrm{2}\right)\left({t}+\mathrm{3}\right)..\left({t}+{n}\right)} \\ $$$$\frac{\mathrm{1}}{\left({t}+\mathrm{1}\right)\left({t}+\mathrm{2}\right)\left({t}+\mathrm{3}\right)..\left({t}+{n}\right)}=\frac{{a}_{\mathrm{1}} }{{t}+\mathrm{1}}+\frac{{a}_{\mathrm{2}} }{{t}+\mathrm{2}}+..+\frac{{a}_{{n}} }{\left({t}+{n}\right)} \\ $$$$\int_{\mathrm{0}} ^{\infty} \left(\frac{{a}_{\mathrm{1}} }{{t}+\mathrm{1}}+\frac{{a}_{\mathrm{2}} }{{t}+\mathrm{2}}+..+\frac{{a}_{{n}} }{{t}+{n}}\right){dt} \\ $$$$=\mid{a}_{\mathrm{1}} {ln}\left({t}+\mathrm{1}\right)+{a}_{\mathrm{2}} {ln}\left({t}+\mathrm{2}\right)+..+{a}_{{n}} {ln}\left({t}+{n}\right)\mid_{\mathrm{0}} ^{\infty} \\ $$$${now}\:{calculation}\:{to}\:{find}\:{a}_{\mathrm{1}} ,{a}_{\mathrm{2}} …{a}_{{n}} \\ $$$$\mathrm{1}={a}_{\mathrm{1}} \left({t}+\mathrm{2}\right)\left({t}+\mathrm{3}\right)..\left({t}+{n}\right)+{a}_{\mathrm{2}} \left({t}+\mathrm{1}\right)\left({t}+\mathrm{3}\right)..\left({t}+{n}\right)+..{a}_{{n}} \left({t}+\mathrm{1}\right)\left({t}+\mathrm{2}\right)..\left({t}+{n}−\mathrm{1}\right) \\ $$$${put}\:{t}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{1}={a}_{\mathrm{1}} ×\left({n}−\mathrm{1}\right)!\rightarrow{a}_{\mathrm{1}} =\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!} \\ $$$${put}\:{t}+\mathrm{2}=\mathrm{0} \\ $$$${a}_{\mathrm{2}} ×\left(−\mathrm{2}+\mathrm{1}\right)\left(\mathrm{1}.\mathrm{2}…{n}−\mathrm{2}\right) \\ $$$${a}_{\mathrm{2}} ×\left(−\mathrm{1}\right)\left({n}−\mathrm{2}\right)!=\mathrm{1}\rightarrow{a}_{\mathrm{2}} =\frac{\mathrm{1}}{\left(−\mathrm{1}\right)\left({n}−\mathrm{2}\right)!} \\ $$$${put}\:{t}+\mathrm{3}=\mathrm{0} \\ $$$${a}_{\mathrm{3}} \left({t}+\mathrm{1}\right)\left({t}+\mathrm{2}\right)\left({t}+\mathrm{4}\right)…\left({t}+{n}\right)=\mathrm{1} \\ $$$${a}_{\mathrm{3}} \left(−\mathrm{3}+\mathrm{1}\right)\left(−\mathrm{3}+\mathrm{2}\right)\left(\mathrm{1}.\mathrm{2}….{n}−\mathrm{3}\right)=\mathrm{1} \\ $$$${a}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}×\left({n}−\mathrm{3}\right)!} \\ $$$${tried}\:{to}\:{solve} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *