Question Number 133275 by mr W last updated on 20/Feb/21

Commented by mr W last updated on 20/Feb/21

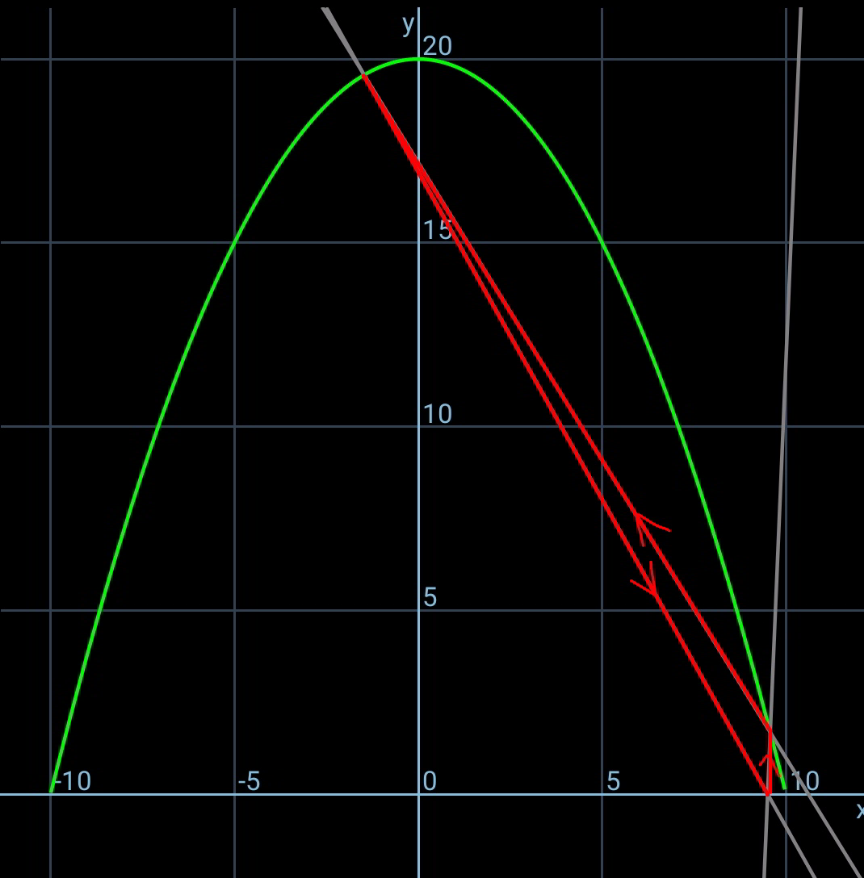
$${A}\:{hall}\:{with}\:{horizontal}\:{smooth}\:{floor} \\ $$$${has}\:{a}\:{parabola}\:{shaped}\:{wall}\:{as}\:{shown}. \\ $$$${A}\:{ball}\:{is}\:{projected}\:{along}\:{the}\:{floor} \\ $$$${from}\:{point}\:{A}\:{and}\:{returns}\:{back}\:{to}\:{this} \\ $$$${point}\:{after}\:{two}\:{impacts}\:{with}\:{the}\:{wall}. \\ $$$${If}\:{the}\:{impacts}\:{are}\:{elastic},\:{find}\:{the} \\ $$$${coordinates}\:{of}\:{the}\:{impact}\:{points}\:{B} \\ $$$${and}\:{C}. \\ $$
Answered by mr W last updated on 21/Feb/21

Commented by mr W last updated on 21/Feb/21

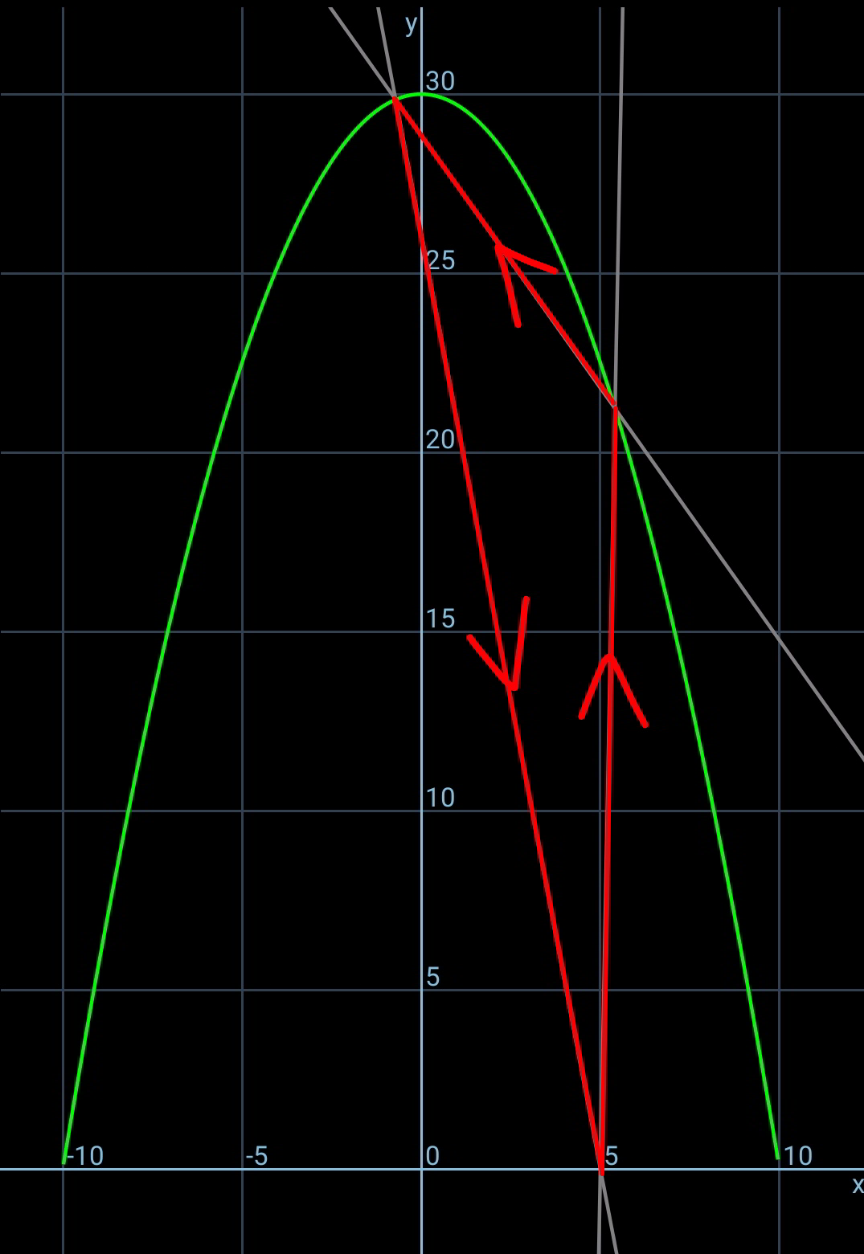
$${since}\:{the}\:{impacts}\:{are}\:{elastic},\:{the} \\ $$$${path}\:{of}\:{the}\:{ball}\:{is}\:{the}\:{same}\:{as}\:{of}\:{a} \\ $$$${light}\:{ray}. \\ $$$${A}'\:={image}\:{of}\:{A}\:{in}\:{tangent}\:{at}\:{B} \\ $$$${A}''\:={image}\:{of}\:{A}\:{in}\:{tangent}\:{at}\:{C} \\ $$$${then}\:{A}',\:{B},\:{C}\:{and}\:{A}''\:{are}\:{collinear}. \\ $$$$ \\ $$$${let}\:\eta=\frac{{h}}{{b}},\:\xi=\frac{{a}}{{b}},\:\lambda=\frac{{p}}{{b}},\:\mu=\frac{{q}}{{b}} \\ $$$${equation}\:{of}\:{parabola}: \\ $$$${y}={h}−\frac{{hx}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$$\frac{{dy}}{{dx}}=−\frac{\mathrm{2}{hx}}{{b}^{\mathrm{2}} } \\ $$$${say}\:{B}\left({p},\:{y}_{{B}} \right)\:{with}\:{y}_{{B}} ={h}−\frac{{hp}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$${say}\:{C}\left({q},\:{y}_{{B}} \right)\:{with}\:{y}_{{C}} ={h}−\frac{{hq}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{2}{hp}}{{b}^{\mathrm{2}} }=\mathrm{2}\eta\lambda \\ $$$$\mathrm{tan}\:\varphi=−\frac{\mathrm{2}{hq}}{{b}^{\mathrm{2}} }=−\mathrm{2}\eta\mu \\ $$$$\mathrm{tan}\:\alpha=\frac{{y}_{{B}} }{{p}−{a}}=\frac{{h}−\frac{{hp}^{\mathrm{2}} }{{b}^{\mathrm{2}} }}{{p}−{a}}=\frac{\eta\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)}{\lambda−\xi} \\ $$$$\mathrm{tan}\:\beta=\frac{{y}_{{C}} }{{a}−{q}}=\frac{{h}−\frac{{hq}^{\mathrm{2}} }{{b}^{\mathrm{2}} }}{{a}−{q}}=\frac{\eta\left(\mathrm{1}−\mu^{\mathrm{2}} \right)}{\xi−\mu} \\ $$$$\mathrm{tan}\:\phi=\frac{{y}_{{C}} −{y}_{{B}} }{{p}−{q}}=\frac{−\frac{{hq}^{\mathrm{2}} }{{b}^{\mathrm{2}} }+\frac{{hp}^{\mathrm{2}} }{{b}^{\mathrm{2}} }}{{p}−{q}}=\eta\left(\lambda+\mu\right) \\ $$$$\gamma=\pi−\alpha−\theta \\ $$$$\delta=\pi−\beta−\varphi \\ $$$$ \\ $$$$\gamma+\phi=\theta \\ $$$$\pi−\left(\alpha−\phi\right)=\mathrm{2}\theta \\ $$$$\mathrm{tan}\:\mathrm{2}\theta=−\mathrm{tan}\:\left(\alpha−\phi\right) \\ $$$$\frac{\mathrm{2}\:\mathrm{tan}\:\theta}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\theta}=−\frac{\mathrm{tan}\:\alpha−\mathrm{tan}\:\phi}{\mathrm{1}+\mathrm{tan}\:\alpha\:\mathrm{tan}\:\phi} \\ $$$$\frac{\mathrm{2}×\mathrm{2}\eta\lambda}{\mathrm{1}−\left(\mathrm{2}\eta\lambda\right)^{\mathrm{2}} }=−\frac{\frac{\eta\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)}{\lambda−\xi}−\eta\left(\lambda+\mu\right)}{\mathrm{1}+\frac{\eta\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)}{\lambda−\xi}×\eta\left(\lambda+\mu\right)} \\ $$$$\frac{\mathrm{4}\lambda}{\mathrm{1}−\mathrm{4}\eta^{\mathrm{2}} \lambda^{\mathrm{2}} }+\frac{\mathrm{1}−\lambda^{\mathrm{2}} −\left(\lambda+\mu\right)\left(\lambda−\xi\right)}{\lambda−\xi+\eta^{\mathrm{2}} \left(\mathrm{1}−\lambda^{\mathrm{2}} \right)\left(\lambda+\mu\right)}=\mathrm{0}\:\:\:…\left({i}\right) \\ $$$$ \\ $$$$\delta−\phi=\varphi \\ $$$$\pi−\left(\beta+\phi\right)=\mathrm{2}\varphi \\ $$$$\mathrm{tan}\:\mathrm{2}\varphi=−\mathrm{tan}\:\left(\beta+\phi\right) \\ $$$$\frac{\mathrm{2}\:\mathrm{tan}\:\varphi}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\varphi}=−\frac{\mathrm{tan}\:\beta+\mathrm{tan}\:\phi}{\mathrm{1}−\mathrm{tan}\:\beta\:\mathrm{tan}\:\phi} \\ $$$$\frac{\mathrm{2}\left(−\mathrm{2}\eta\mu\right)}{\mathrm{1}−\left(−\mathrm{2}\eta\mu\right)^{\mathrm{2}} }=−\frac{\frac{\eta\left(\mathrm{1}−\mu^{\mathrm{2}} \right)}{\xi−\mu}+\eta\left(\lambda+\mu\right)}{\mathrm{1}−\frac{\eta\left(\mathrm{1}−\mu^{\mathrm{2}} \right)}{\xi−\mu}×\eta\left(\lambda+\mu\right)} \\ $$$$\frac{\mathrm{4}\mu}{\mathrm{1}−\mathrm{4}\eta^{\mathrm{2}} \mu^{\mathrm{2}} }+\frac{\mathrm{1}−\mu^{\mathrm{2}} +\left(\lambda+\mu\right)\left(\xi−\mu\right)}{\mu−\xi+\eta^{\mathrm{2}} \left(\mathrm{1}−\mu^{\mathrm{2}} \right)\left(\lambda+\mu\right)}=\mathrm{0}\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$${from}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{we}\:{get}\:\lambda\:{and}\:\mu. \\ $$$$ \\ $$$${examples}: \\ $$
Commented by mr W last updated on 21/Feb/21

Commented by mr W last updated on 21/Feb/21

Commented by mr W last updated on 21/Feb/21

Commented by mr W last updated on 21/Feb/21
Commented by mr W last updated on 21/Feb/21

Commented by mr W last updated on 21/Feb/21

Commented by mr W last updated on 21/Feb/21