Menu Close

find-the-infinite-sum-n-0-F-n-2-n-where-F-n-1-5-1-5-2-n-1-1-5-1-5-2-n-1-

Tinku Tara 0 Comments
Pin




Question Number 90609 by Maclaurin Stickker last updated on 25/Apr/20
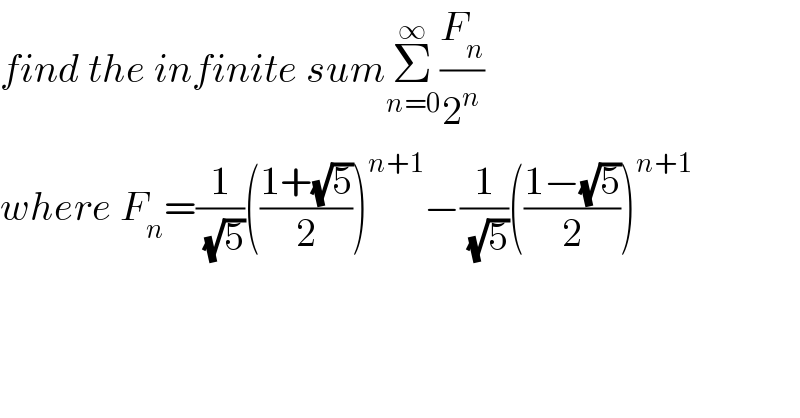
find the infinite sumΣ_(n=0) ^∞ (F_n /2^n ) where F_n =(1/( (√5)))(((1+(√5))/2))^(n+1) −(1/( (√5)))(((1−(√5))/2))^(n+1)
$${find}\:{the}\:{infinite}\:{sum}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{F}_{{n}} }{\mathrm{2}^{{n}} }\: \\ $$$${where}\:{F}_{{n}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}+\mathrm{1}} −\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}+\mathrm{1}} \\ $$
Commented by abdomathmax last updated on 25/Apr/20
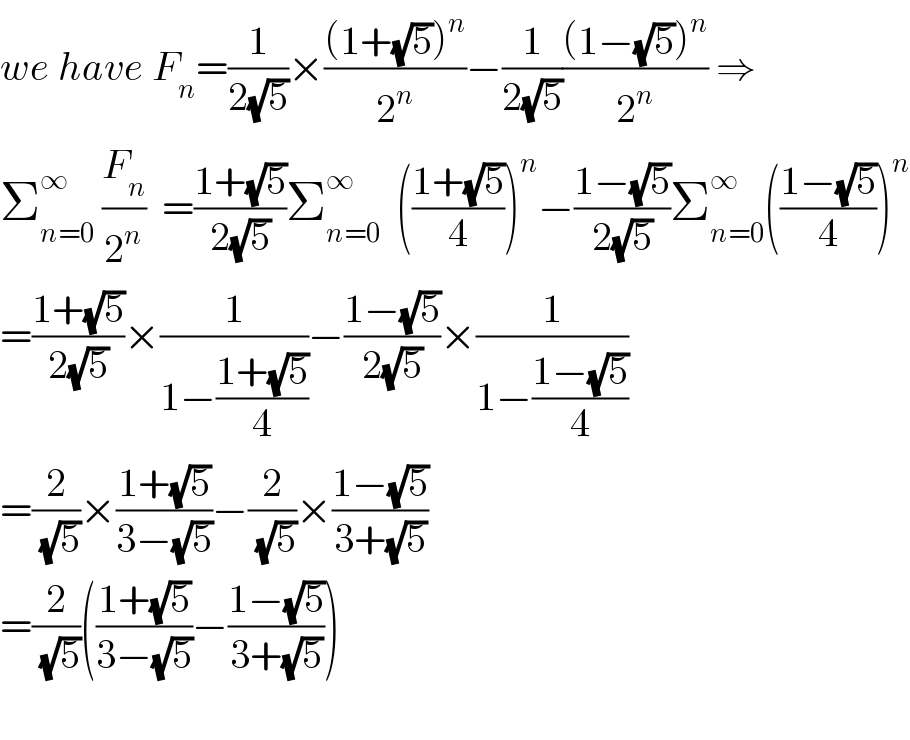
we have F_n =(1/(2(√5)))×(((1+(√5))^n )/2^n )−(1/(2(√5)))(((1−(√5))^n )/2^n ) ⇒ Σ_(n=0) ^∞ (F_n /2^n ) =((1+(√5))/(2(√5)))Σ_(n=0) ^∞ (((1+(√5))/4))^n −((1−(√5))/(2(√5)))Σ_(n=0) ^∞ (((1−(√5))/4))^n =((1+(√5))/(2(√5)))×(1/(1−((1+(√5))/4)))−((1−(√5))/(2(√5)))×(1/(1−((1−(√5))/4))) =(2/( (√5)))×((1+(√5))/(3−(√5)))−(2/( (√5)))×((1−(√5))/(3+(√5))) =(2/( (√5)))(((1+(√5))/(3−(√5)))−((1−(√5))/(3+(√5))))
$${we}\:{have}\:{F}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{5}}}×\frac{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)^{{n}} }{\mathrm{2}^{{n}} }−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{5}}}\frac{\left(\mathrm{1}−\sqrt{\mathrm{5}}\right)^{{n}} }{\mathrm{2}^{{n}} }\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{F}_{{n}} }{\mathrm{2}^{{n}} }\:\:=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}\sqrt{\mathrm{5}}}\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\right)^{{n}} −\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}\sqrt{\mathrm{5}}}\sum_{{n}=\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}}\right)^{{n}} \\ $$$$=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}\sqrt{\mathrm{5}}}×\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}}−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}\sqrt{\mathrm{5}}}×\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}×\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{3}−\sqrt{\mathrm{5}}}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}×\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{3}+\sqrt{\mathrm{5}}} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{3}−\sqrt{\mathrm{5}}}−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{3}+\sqrt{\mathrm{5}}}\right) \\ $$$$ \\ $$
Commented by Maclaurin Sticcker last updated on 25/Apr/20
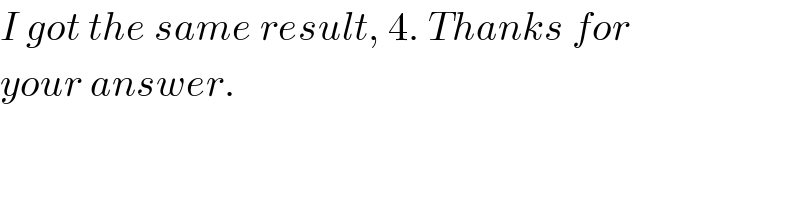
I got the same result, 4. Thanks for your answer.
$${I}\:{got}\:{the}\:{same}\:{result},\:\mathrm{4}.\:{Thanks}\:{for} \\ $$$${your}\:{answer}. \\ $$
Commented by abdomathmax last updated on 25/Apr/20
you are welcome
$${you}\:{are}\:{welcome} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *