0-1-x-1-x-1-1-x-dx-

Question Number 156206 by mnjuly1970 last updated on 09/Oct/21

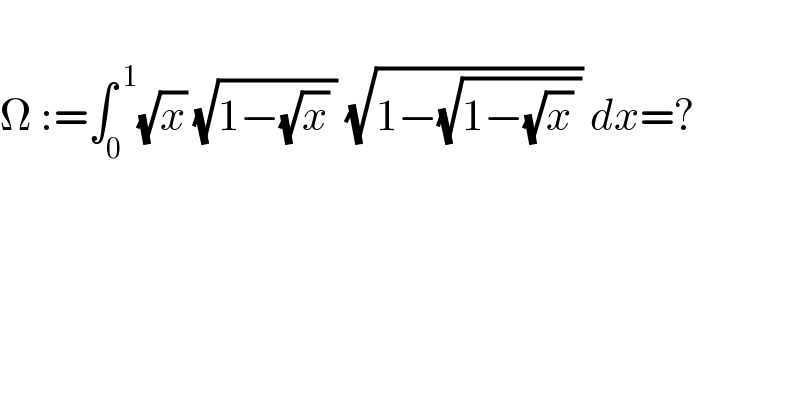
Ω :=∫_0 ^( 1) (√x) (√(1−(√x) )) (√(1−(√(1−(√x) )))) dx=?

$$ \\ $$$$\Omega\::=\int_{\mathrm{0}} ^{\:\mathrm{1}} \sqrt{{x}}\:\sqrt{\mathrm{1}−\sqrt{{x}}\:}\:\sqrt{\mathrm{1}−\sqrt{\mathrm{1}−\sqrt{{x}}\:}}\:{dx}=? \\ $$

Answered by mindispower last updated on 09/Oct/21

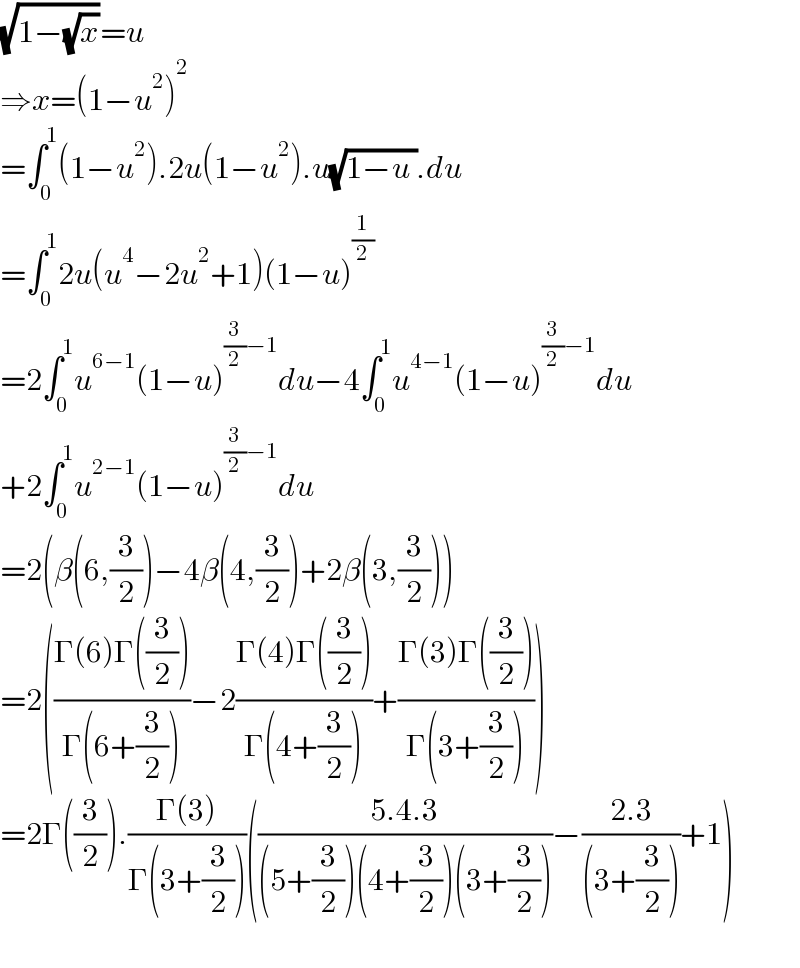
(√(1−(√x)))=u ⇒x=(1−u^2 )^2 =∫_0 ^1 (1−u^2 ).2u(1−u^2 ).u(√(1−u )).du =∫_0 ^1 2u(u^4 −2u^2 +1)(1−u)^(1/2) =2∫_0 ^1 u^(6−1) (1−u)^((3/2)−1) du−4∫_0 ^1 u^(4−1) (1−u)^((3/2)−1) du +2∫_0 ^1 u^(2−1) (1−u)^((3/2)−1) du =2(β(6,(3/2))−4β(4,(3/2))+2β(3,(3/2))) =2(((Γ(6)Γ((3/2)))/(Γ(6+(3/2))))−2((Γ(4)Γ((3/2)))/(Γ(4+(3/2))))+((Γ(3)Γ((3/2)))/(Γ(3+(3/2))))) =2Γ((3/2)).((Γ(3))/(Γ(3+(3/2))))(((5.4.3)/((5+(3/2))(4+(3/2))(3+(3/2))))−((2.3)/((3+(3/2))))+1)

$$\sqrt{\mathrm{1}−\sqrt{{x}}}={u} \\ $$$$\Rightarrow{x}=\left(\mathrm{1}−{u}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{u}^{\mathrm{2}} \right).\mathrm{2}{u}\left(\mathrm{1}−{u}^{\mathrm{2}} \right).{u}\sqrt{\mathrm{1}−{u}\:}.{du} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{2}{u}\left({u}^{\mathrm{4}} −\mathrm{2}{u}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{1}−{u}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{\mathrm{6}−\mathrm{1}} \left(\mathrm{1}−{u}\right)^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}} {du}−\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{\mathrm{4}−\mathrm{1}} \left(\mathrm{1}−{u}\right)^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}} {du} \\ $$$$+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{\mathrm{2}−\mathrm{1}} \left(\mathrm{1}−{u}\right)^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}} {du} \\ $$$$=\mathrm{2}\left(\beta\left(\mathrm{6},\frac{\mathrm{3}}{\mathrm{2}}\right)−\mathrm{4}\beta\left(\mathrm{4},\frac{\mathrm{3}}{\mathrm{2}}\right)+\mathrm{2}\beta\left(\mathrm{3},\frac{\mathrm{3}}{\mathrm{2}}\right)\right) \\ $$$$=\mathrm{2}\left(\frac{\Gamma\left(\mathrm{6}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{6}+\frac{\mathrm{3}}{\mathrm{2}}\right)}−\mathrm{2}\frac{\Gamma\left(\mathrm{4}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{4}+\frac{\mathrm{3}}{\mathrm{2}}\right)}+\frac{\Gamma\left(\mathrm{3}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{3}+\frac{\mathrm{3}}{\mathrm{2}}\right)}\right) \\ $$$$=\mathrm{2}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right).\frac{\Gamma\left(\mathrm{3}\right)}{\Gamma\left(\mathrm{3}+\frac{\mathrm{3}}{\mathrm{2}}\right)}\left(\frac{\mathrm{5}.\mathrm{4}.\mathrm{3}}{\left(\mathrm{5}+\frac{\mathrm{3}}{\mathrm{2}}\right)\left(\mathrm{4}+\frac{\mathrm{3}}{\mathrm{2}}\right)\left(\mathrm{3}+\frac{\mathrm{3}}{\mathrm{2}}\right)}−\frac{\mathrm{2}.\mathrm{3}}{\left(\mathrm{3}+\frac{\mathrm{3}}{\mathrm{2}}\right)}+\mathrm{1}\right) \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 09/Oct/21

$${grateful}\:{sir}\:{power}\:… \\ $$

Commented by mindispower last updated on 09/Oct/21

$${withe}\:{pleasur}\:{sir}\: \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply