Question Number 90700 by jagoll last updated on 25/Apr/20
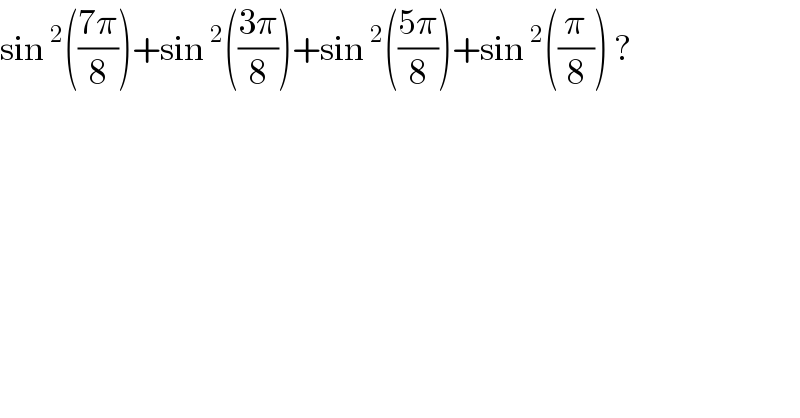
$$\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{7}\pi}{\mathrm{8}}\right)+\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)+\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{5}\pi}{\mathrm{8}}\right)+\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}\right)\:? \\ $$
Commented by john santu last updated on 25/Apr/20
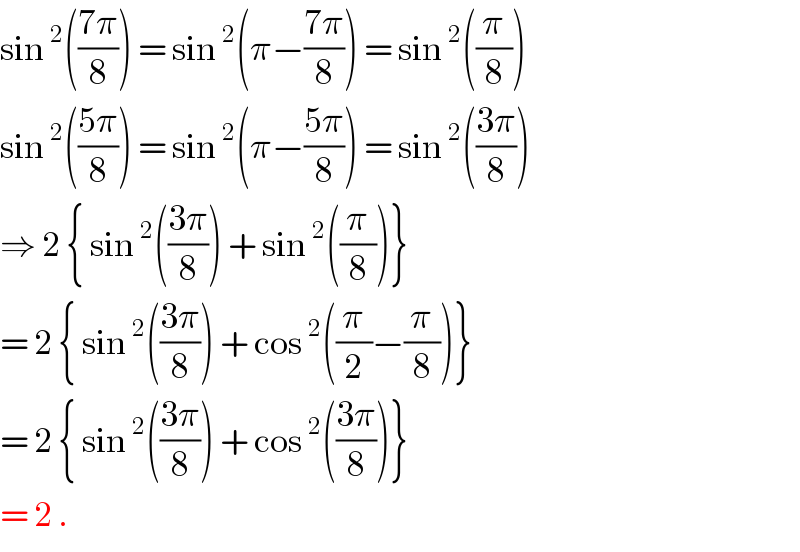
$$\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{7}\pi}{\mathrm{8}}\right)\:=\:\mathrm{sin}\:^{\mathrm{2}} \left(\pi−\frac{\mathrm{7}\pi}{\mathrm{8}}\right)\:=\:\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}\right) \\ $$$$\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{5}\pi}{\mathrm{8}}\right)\:=\:\mathrm{sin}\:^{\mathrm{2}} \left(\pi−\frac{\mathrm{5}\pi}{\mathrm{8}}\right)\:=\:\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right) \\ $$$$\Rightarrow\:\mathrm{2}\:\left\{\:\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\:+\:\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}\right)\right\} \\ $$$$=\:\mathrm{2}\:\left\{\:\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\:+\:\mathrm{cos}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{8}}\right)\right\} \\ $$$$=\:\mathrm{2}\:\left\{\:\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\:+\:\mathrm{cos}\:^{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\right\}\: \\ $$$$=\:\mathrm{2}\:.\: \\ $$
Commented by jagoll last updated on 25/Apr/20

$${thank}\:{you} \\ $$
Commented by peter frank last updated on 26/Apr/20

$${thanks} \\ $$
