Menu Close

Question-25343

Tinku Tara 0 Comments
Pin




Question Number 25343 by Tinkutara last updated on 08/Dec/17
Commented by sushmitak last updated on 08/Dec/17
As pointed out below. This is incorrect logic. The correct logic for interchangable variables in an equation is that if p is a solutoon for b then it must be a solution for c. It need not be simulaneously true for b and c. If you swap b and c equation does not change so b=c (1/(2cos A))=2−2cosA 4cos^2 A−4cos A+1=0 cos A=((4±(√(4^2 −16)))/8)=(1/2) cos A=60 b=c⇒B=C=60
$${As}\:{pointed}\:{out}\:{below}.\:{This} \\ $$$${is}\:{incorrect}\:{logic}. \\ $$$${The}\:{correct}\:{logic}\:{for}\:{interchangable} \\ $$$${variables}\:{in}\:{an}\:{equation}\:{is}\:{that} \\ $$$${if}\:{p}\:{is}\:{a}\:{solutoon}\:{for}\:{b}\:{then}\:{it} \\ $$$${must}\:{be}\:{a}\:{solution}\:{for}\:{c}. \\ $$$${It}\:{need}\:{not}\:{be}\:{simulaneously}\:{true} \\ $$$${for}\:{b}\:{and}\:{c}. \\ $$$$\mathrm{If}\:\mathrm{you}\:\mathrm{swap}\:{b}\:\mathrm{and}\:{c}\:\mathrm{equation}\:\mathrm{does} \\ $$$$\mathrm{not}\:\mathrm{change}\:\mathrm{so}\:{b}={c} \\ $$$$\frac{\mathrm{1}}{\mathrm{2cos}\:{A}}=\mathrm{2}−\mathrm{2cos}{A} \\ $$$$\mathrm{4cos}^{\mathrm{2}} {A}−\mathrm{4cos}\:{A}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{cos}\:{A}=\frac{\mathrm{4}\pm\sqrt{\mathrm{4}^{\mathrm{2}} −\mathrm{16}}}{\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:{A}=\mathrm{60} \\ $$$${b}={c}\Rightarrow{B}={C}=\mathrm{60} \\ $$
Commented by ajfour last updated on 08/Dec/17
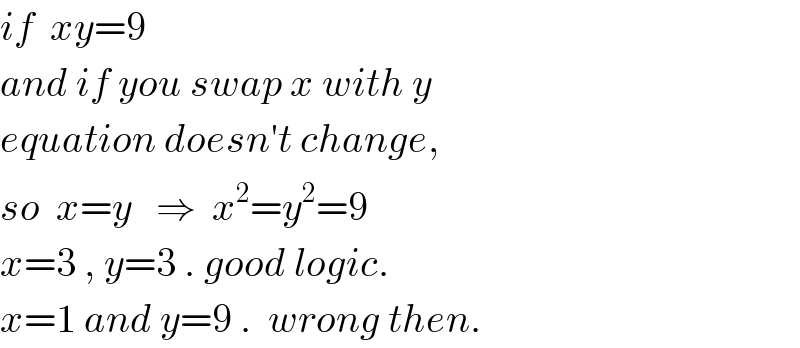
if xy=9 and if you swap x with y equation doesn′t change, so x=y ⇒ x^2 =y^2 =9 x=3 , y=3 . good logic. x=1 and y=9 . wrong then.
$${if}\:\:{xy}=\mathrm{9} \\ $$$${and}\:{if}\:{you}\:{swap}\:{x}\:{with}\:{y} \\ $$$${equation}\:{doesn}'{t}\:{change}, \\ $$$${so}\:\:{x}={y}\:\:\:\Rightarrow\:\:{x}^{\mathrm{2}} ={y}^{\mathrm{2}} =\mathrm{9} \\ $$$${x}=\mathrm{3}\:,\:{y}=\mathrm{3}\:.\:{good}\:{logic}. \\ $$$${x}=\mathrm{1}\:{and}\:{y}=\mathrm{9}\:.\:\:{wrong}\:{then}. \\ $$
Commented by sushmitak last updated on 08/Dec/17
Thanks.
$$\mathrm{Thanks}. \\ $$
Commented by Rasheed.Sindhi last updated on 08/Dec/17
If the triangle is an equilateral: Let a=b=c=x (x^2 /(2 cos A))=2x^2 −2x^2 cos A (1/(2 cos A))=2−2cos A 4 cosA−4cos^2 A=1 4cos^2 A−4 cosA+1=0 4cos^2 A−2 cosA−2 cosA+1=0 2 cosA(2 cosA−1)−1(2 cosA−1)=0 (2 cosA−1)^2 =0 cosA=(1/2)⇒A=60 Continue
$$\mathrm{If}\:\mathrm{the}\:\mathrm{triangle}\:\mathrm{is}\:\mathrm{an}\:\mathrm{equilateral}: \\ $$$$\mathrm{Let}\:\mathrm{a}=\mathrm{b}=\mathrm{c}=\mathrm{x} \\ $$$$\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}\:\mathrm{cos}\:\mathrm{A}}=\mathrm{2x}^{\mathrm{2}} −\mathrm{2x}^{\mathrm{2}} \mathrm{cos}\:\mathrm{A} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{A}}=\mathrm{2}−\mathrm{2cos}\:\mathrm{A} \\ $$$$\mathrm{4}\:\mathrm{cosA}−\mathrm{4cos}^{\mathrm{2}} \:\mathrm{A}=\mathrm{1} \\ $$$$\mathrm{4cos}^{\mathrm{2}} \:\mathrm{A}−\mathrm{4}\:\mathrm{cosA}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{4cos}^{\mathrm{2}} \:\mathrm{A}−\mathrm{2}\:\mathrm{cosA}−\mathrm{2}\:\mathrm{cosA}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{2}\:\mathrm{cosA}\left(\mathrm{2}\:\mathrm{cosA}−\mathrm{1}\right)−\mathrm{1}\left(\mathrm{2}\:\mathrm{cosA}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\left(\mathrm{2}\:\mathrm{cosA}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{cosA}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{A}=\mathrm{60} \\ $$$$\mathrm{Continue} \\ $$
Commented by Rasheed.Sindhi last updated on 08/Dec/17
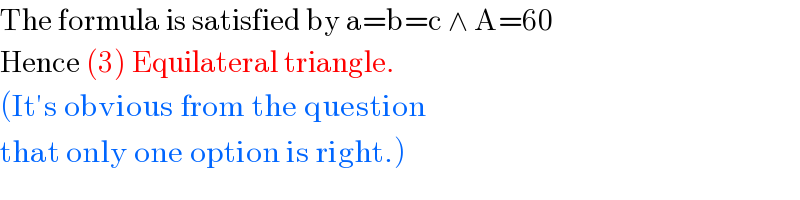
The formula is satisfied by a=b=c ∧ A=60 Hence (3) Equilateral triangle. (It′s obvious from the question that only one option is right.)
$$\mathrm{The}\:\mathrm{formula}\:\mathrm{is}\:\mathrm{satisfied}\:\mathrm{by}\:\mathrm{a}=\mathrm{b}=\mathrm{c}\:\wedge\:\mathrm{A}=\mathrm{60}\: \\ $$$$\mathrm{Hence}\:\left(\mathrm{3}\right)\:\mathrm{Equilateral}\:\mathrm{triangle}. \\ $$$$\left(\mathrm{It}'\mathrm{s}\:\mathrm{obvious}\:\mathrm{from}\:\mathrm{the}\:\mathrm{question}\right. \\ $$$$\left.\mathrm{that}\:\mathrm{only}\:\mathrm{one}\:\mathrm{option}\:\mathrm{is}\:\mathrm{right}.\right) \\ $$
Answered by ajfour last updated on 08/Dec/17
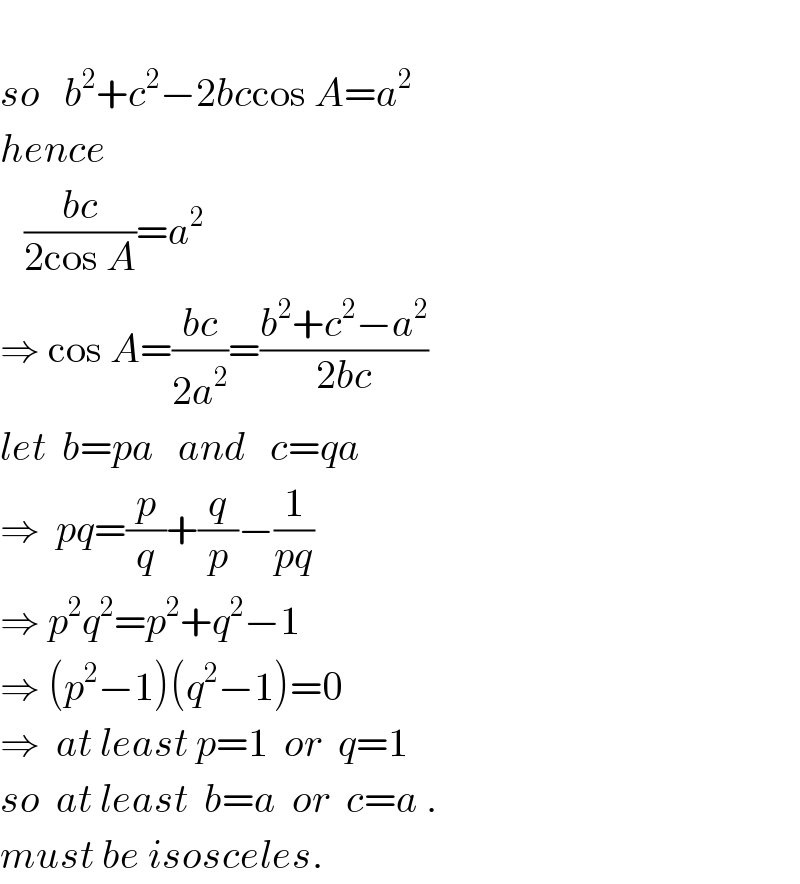
so b^2 +c^2 −2bccos A=a^2 hence ((bc)/(2cos A))=a^2 ⇒ cos A=((bc)/(2a^2 ))=((b^2 +c^2 −a^2 )/(2bc)) let b=pa and c=qa ⇒ pq=(p/q)+(q/p)−(1/(pq)) ⇒ p^2 q^2 =p^2 +q^2 −1 ⇒ (p^2 −1)(q^2 −1)=0 ⇒ at least p=1 or q=1 so at least b=a or c=a . must be isosceles.
$$ \\ $$$${so}\:\:\:{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}\mathrm{cos}\:{A}={a}^{\mathrm{2}} \\ $$$${hence} \\ $$$$\:\:\:\frac{{bc}}{\mathrm{2cos}\:{A}}={a}^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{cos}\:{A}=\frac{{bc}}{\mathrm{2}{a}^{\mathrm{2}} }=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}} \\ $$$${let}\:\:{b}={pa}\:\:\:{and}\:\:\:{c}={qa} \\ $$$$\Rightarrow\:\:{pq}=\frac{{p}}{{q}}+\frac{{q}}{{p}}−\frac{\mathrm{1}}{{pq}} \\ $$$$\Rightarrow\:{p}^{\mathrm{2}} {q}^{\mathrm{2}} ={p}^{\mathrm{2}} +{q}^{\mathrm{2}} −\mathrm{1} \\ $$$$\Rightarrow\:\left({p}^{\mathrm{2}} −\mathrm{1}\right)\left({q}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:{at}\:{least}\:{p}=\mathrm{1}\:\:{or}\:\:{q}=\mathrm{1} \\ $$$${so}\:\:{at}\:{least}\:\:{b}={a}\:\:{or}\:\:{c}={a}\:. \\ $$$${must}\:{be}\:{isosceles}. \\ $$
Commented by Tinkutara last updated on 09/Dec/17
Thank you Sir!
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *