Menu Close

Find-x-sin-3x-sin-2x-2sin-x-3-cos-x-

Tinku Tara 0 Comments
Pin




Question Number 133321 by 777316 last updated on 21/Feb/21
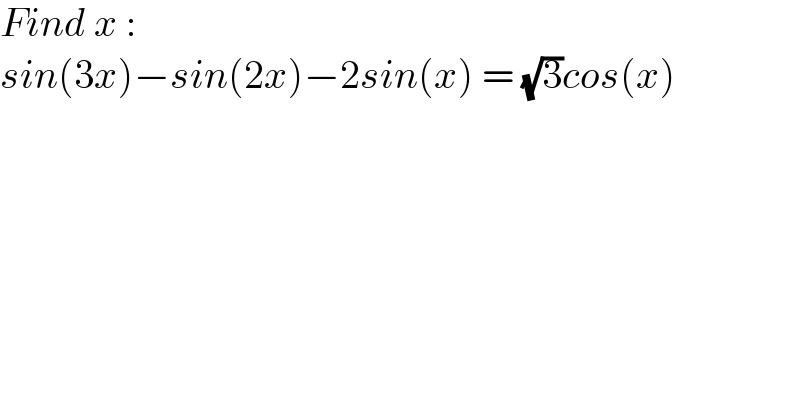
Find x : sin(3x)−sin(2x)−2sin(x) = (√3)cos(x)
$${Find}\:{x}\:: \\ $$$${sin}\left(\mathrm{3}{x}\right)−{sin}\left(\mathrm{2}{x}\right)−\mathrm{2}{sin}\left({x}\right)\:=\:\sqrt{\mathrm{3}}{cos}\left({x}\right) \\ $$
Commented by bramlexs22 last updated on 21/Feb/21
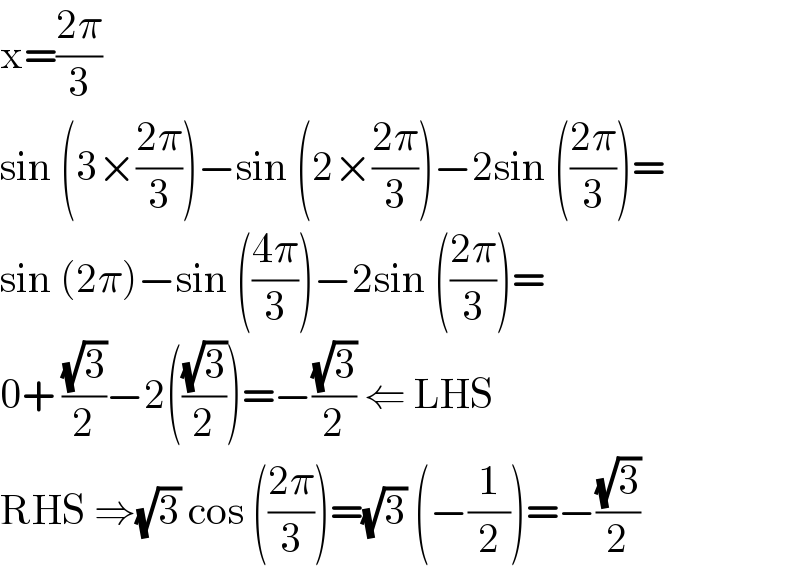
x=((2π)/3) sin (3×((2π)/3))−sin (2×((2π)/3))−2sin (((2π)/3))= sin (2π)−sin (((4π)/3))−2sin (((2π)/3))= 0+ ((√3)/2)−2(((√3)/2))=−((√3)/2) ⇐ LHS RHS ⇒(√3) cos (((2π)/3))=(√3) (−(1/2))=−((√3)/2)
$$\mathrm{x}=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\mathrm{sin}\:\left(\mathrm{3}×\frac{\mathrm{2}\pi}{\mathrm{3}}\right)−\mathrm{sin}\:\left(\mathrm{2}×\frac{\mathrm{2}\pi}{\mathrm{3}}\right)−\mathrm{2sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)= \\ $$$$\mathrm{sin}\:\left(\mathrm{2}\pi\right)−\mathrm{sin}\:\left(\frac{\mathrm{4}\pi}{\mathrm{3}}\right)−\mathrm{2sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)= \\ $$$$\mathrm{0}+\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\mathrm{2}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)=−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Leftarrow\:\mathrm{LHS} \\ $$$$\mathrm{RHS}\:\Rightarrow\sqrt{\mathrm{3}}\:\mathrm{cos}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)=\sqrt{\mathrm{3}}\:\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)=−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$
Answered by bramlexs22 last updated on 21/Feb/21
x=((2π)/3), ((8π)/3),((14π)/3),...
$$\mathrm{x}=\frac{\mathrm{2}\pi}{\mathrm{3}},\:\frac{\mathrm{8}\pi}{\mathrm{3}},\frac{\mathrm{14}\pi}{\mathrm{3}},…\: \\ $$
Commented by 777316 last updated on 21/Feb/21
how
Commented by bramlexs22 last updated on 21/Feb/21
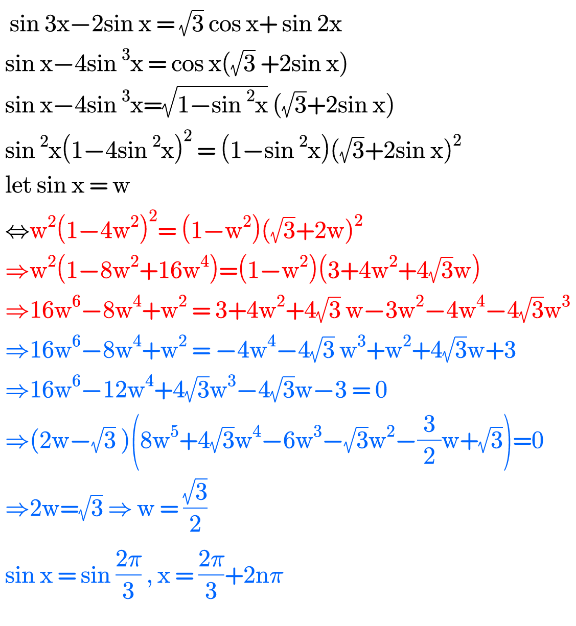
Answered by MJS_new last updated on 21/Feb/21
sin 3x −sin 2x −sin x =(√3)cos x ... ±(4cos^2 x −2cos x −3)(√(1−cos^2 x)) =(√3)cos x let c=cos x squaring and transforming c^6 −c^5 −(9/4)c^4 +(7/4)c^3 +2c^2 −(3/4)c−(9/(16))=0 (c+(1/2))(c^5 −(3/2)c^4 −(3/2)c^3 +(5/2)c^2 +(3/4)c−(9/8))=0 the 5^(th) degree polynome has one real solution we can only approximate c_1 =−(1/2)=cos x_1 c_2 ≈.777106906075 =cos x_2 testing the solutions (because we have squared) leads to ⇒ x_1 =((2π)/3)+2nπ x_2 ≈−.680740465517+2nπ
$$\mathrm{sin}\:\mathrm{3}{x}\:−\mathrm{sin}\:\mathrm{2}{x}\:−\mathrm{sin}\:{x}\:=\sqrt{\mathrm{3}}\mathrm{cos}\:{x} \\ $$$$… \\ $$$$\pm\left(\mathrm{4cos}^{\mathrm{2}} \:{x}\:−\mathrm{2cos}\:{x}\:−\mathrm{3}\right)\sqrt{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:{x}}\:=\sqrt{\mathrm{3}}\mathrm{cos}\:{x} \\ $$$$\mathrm{let}\:{c}=\mathrm{cos}\:{x} \\ $$$$\mathrm{squaring}\:\mathrm{and}\:\mathrm{transforming} \\ $$$${c}^{\mathrm{6}} −{c}^{\mathrm{5}} −\frac{\mathrm{9}}{\mathrm{4}}{c}^{\mathrm{4}} +\frac{\mathrm{7}}{\mathrm{4}}{c}^{\mathrm{3}} +\mathrm{2}{c}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}{c}−\frac{\mathrm{9}}{\mathrm{16}}=\mathrm{0} \\ $$$$\left({c}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left({c}^{\mathrm{5}} −\frac{\mathrm{3}}{\mathrm{2}}{c}^{\mathrm{4}} −\frac{\mathrm{3}}{\mathrm{2}}{c}^{\mathrm{3}} +\frac{\mathrm{5}}{\mathrm{2}}{c}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}{c}−\frac{\mathrm{9}}{\mathrm{8}}\right)=\mathrm{0} \\ $$$$\mathrm{the}\:\mathrm{5}^{\mathrm{th}} \:\mathrm{degree}\:\mathrm{polynome}\:\mathrm{has}\:\mathrm{one}\:\mathrm{real}\:\mathrm{solution}\:\mathrm{we} \\ $$$$\mathrm{can}\:\mathrm{only}\:\mathrm{approximate} \\ $$$${c}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{cos}\:{x}_{\mathrm{1}} \\ $$$${c}_{\mathrm{2}} \approx.\mathrm{777106906075}\:=\mathrm{cos}\:{x}_{\mathrm{2}} \\ $$$$\mathrm{testing}\:\mathrm{the}\:\mathrm{solutions}\:\left(\mathrm{because}\:\mathrm{we}\:\mathrm{have}\:\mathrm{squared}\right) \\ $$$$\mathrm{leads}\:\mathrm{to} \\ $$$$\Rightarrow \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{2}\pi}{\mathrm{3}}+\mathrm{2}{n}\pi \\ $$$${x}_{\mathrm{2}} \approx−.\mathrm{680740465517}+\mathrm{2}{n}\pi \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *