Is-there-a-way-to-evaluate-the-following-S-2-2-2-2-2-

Question Number 2275 by Filup last updated on 13/Nov/15

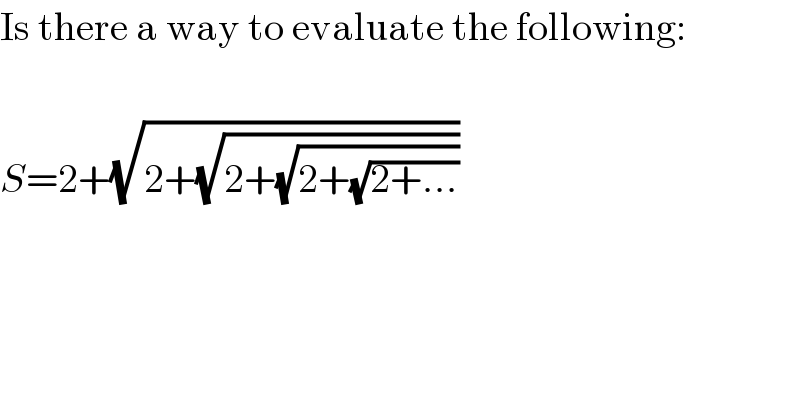
$$\mathrm{Is}\:\mathrm{there}\:\mathrm{a}\:\mathrm{way}\:\mathrm{to}\:\mathrm{evaluate}\:\mathrm{the}\:\mathrm{following}: \\ $$$$ \\ $$$${S}=\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+…}}}} \\ $$

Answered by Rasheed Soomro last updated on 13/Nov/15

$${S}=\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+…}}}} \\ $$$$\left({S}−\mathrm{2}\right)^{\mathrm{2}} =\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+…}}}}\:\right)^{\mathrm{2}} \\ $$$${S}^{\mathrm{2}} −\mathrm{4}{S}+\mathrm{4}\:=\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+…}}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={S} \\ $$$${S}^{\mathrm{2}} −\mathrm{5}{S}+\mathrm{4}=\mathrm{0} \\ $$$$\left({S}−\mathrm{1}\right)\left({S}−\mathrm{4}\right)=\mathrm{0} \\ $$$${S}=\mathrm{1}\:\mid\:\:{S}=\mathrm{4} \\ $$$${Since}\:{we}\:{have}\:{squared}\:{both}\:{sides}\:{the}\:{resulting}\:{equation} \\ $$$${is}\:{not}\:{completely}\:{equivalent}\:{to}\:{the}\:{original}\:{and}\:{there} \\ $$$${is}\:{possibility}\:{of}\:{extraneous}\:{roots}. \\ $$$${Clearly}\:{S}>\mathrm{2}\:{because}\:\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+…}}}}\:{is}\:{positve}. \\ $$$${Hence}\:{S}=\mathrm{1}\:{is}\:{extraneous}\:{root}\:{and} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{S}=\mathrm{4}\:{is}\:{required}\:{sum}. \\ $$

Commented by Filup last updated on 13/Nov/15

$${AMAZING}!\:\mathrm{I}\:\mathrm{am}\:\mathrm{honestly}\:\mathrm{fascinated}! \\ $$

Commented by Filup last updated on 13/Nov/15

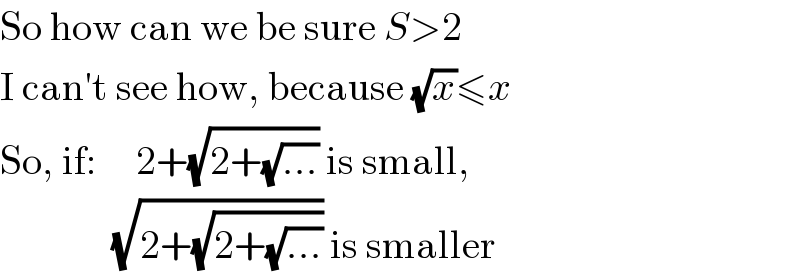
$$\mathrm{So}\:\mathrm{how}\:\mathrm{can}\:\mathrm{we}\:\mathrm{be}\:\mathrm{sure}\:{S}>\mathrm{2} \\ $$$$\mathrm{I}\:\mathrm{can}'\mathrm{t}\:\mathrm{see}\:\mathrm{how},\:\mathrm{because}\:\sqrt{{x}}\leqslant{x} \\ $$$$\mathrm{So},\:\mathrm{if}:\:\:\:\:\:\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{…}}\:\mathrm{is}\:\mathrm{small}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{…}}}\:\mathrm{is}\:\mathrm{smaller} \\ $$

Commented by RasheedAhmad last updated on 13/Nov/15

$${S}=\mathrm{2}+\underset{−−−−−−−−−−−−−−−} {\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+…}}}}}\:\:\:\left[{Given}\right] \\ $$$${Underlined}\:{expression}>\mathrm{0} \\ $$$$\:\therefore\:{S}=\mathrm{2}+{positive}\:{number} \\ $$$$\therefore\:{S}>\mathrm{2} \\ $$

Commented by Filup last updated on 14/Nov/15

$$\mathrm{ahh}\:\mathrm{i}\:\mathrm{must}\:\mathrm{of}\:\mathrm{had}\:\mathrm{a}\:\mathrm{massive}\:\mathrm{brain}\:\mathrm{fart} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com