Menu Close

Question-156869

Tinku Tara 0 Comments
Pin




Question Number 156869 by cortano last updated on 16/Oct/21
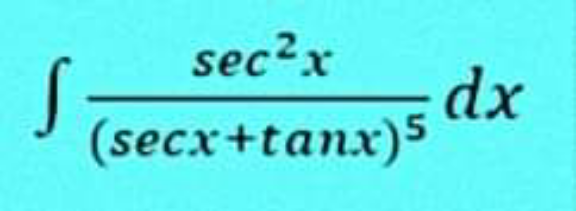
Answered by gsk2684 last updated on 16/Oct/21
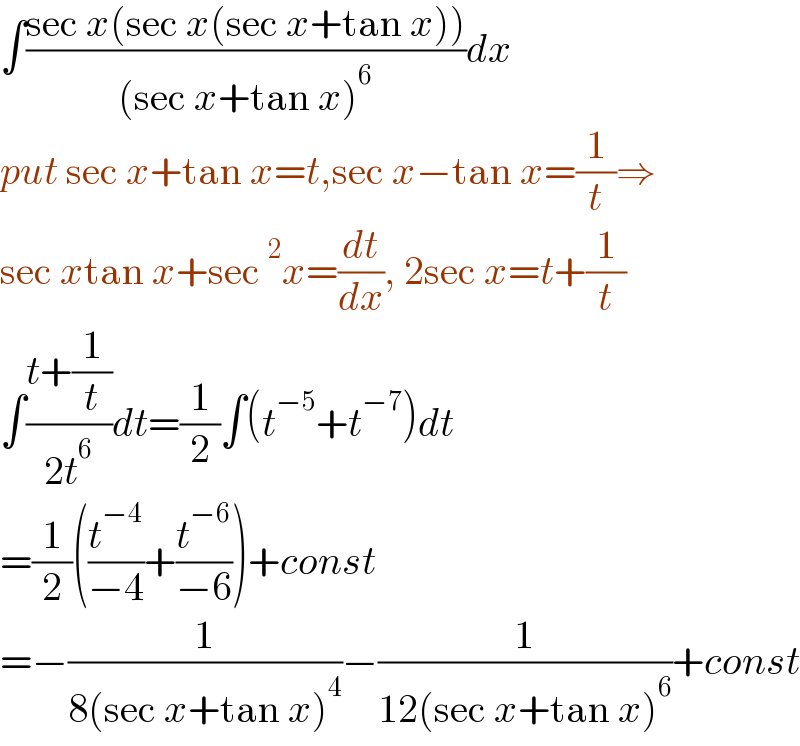
∫((sec x(sec x(sec x+tan x)))/((sec x+tan x)^6 ))dx put sec x+tan x=t,sec x−tan x=(1/t)⇒ sec xtan x+sec^2 x=(dt/dx), 2sec x=t+(1/t) ∫((t+(1/t))/(2t^6 ))dt=(1/2)∫(t^(−5) +t^(−7) )dt =(1/2)((t^(−4) /(−4))+(t^(−6) /(−6)))+const =−(1/(8(sec x+tan x)^4 ))−(1/(12(sec x+tan x)^6 ))+const
$$\int\frac{\mathrm{sec}\:{x}\left(\mathrm{sec}\:{x}\left(\mathrm{sec}\:{x}+\mathrm{tan}\:{x}\right)\right)}{\left(\mathrm{sec}\:{x}+\mathrm{tan}\:{x}\right)^{\mathrm{6}} }{dx} \\ $$$${put}\:\mathrm{sec}\:{x}+\mathrm{tan}\:{x}={t},\mathrm{sec}\:{x}−\mathrm{tan}\:{x}=\frac{\mathrm{1}}{{t}}\Rightarrow \\ $$$$\mathrm{sec}\:{x}\mathrm{tan}\:{x}+\mathrm{sec}\:^{\mathrm{2}} {x}=\frac{{dt}}{{dx}},\:\mathrm{2sec}\:{x}={t}+\frac{\mathrm{1}}{{t}} \\ $$$$\int\frac{{t}+\frac{\mathrm{1}}{{t}}}{\mathrm{2}{t}^{\mathrm{6}} }{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int\left({t}^{−\mathrm{5}} +{t}^{−\mathrm{7}} \right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{t}^{−\mathrm{4}} }{−\mathrm{4}}+\frac{{t}^{−\mathrm{6}} }{−\mathrm{6}}\right)+{const} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{8}\left(\mathrm{sec}\:{x}+\mathrm{tan}\:{x}\right)^{\mathrm{4}} }−\frac{\mathrm{1}}{\mathrm{12}\left(\mathrm{sec}\:{x}+\mathrm{tan}\:{x}\right)^{\mathrm{6}} }+{const} \\ $$
Commented by cortano last updated on 16/Oct/21
yes
$${yes} \\ $$
Answered by puissant last updated on 16/Oct/21
Q=∫((sec^2 x)/((secx+tanx)^5 ))dx = ∫((sec^2 x)/(((1/(cosx))+((sinx)/(cosx)))^5 ))dx =∫((cos^3 x)/((1+sinx)^5 ))dx = ∫(((1−sinx)(1+sinx)cosx)/((1+sinx)^5 ))dx =∫((1−sinx)/((1+sinx)^4 ))cosdx ; u=sinx→du=cosxdx ⇒ Q=∫((1−u)/((1+u)^4 ))du = ∫(1/((1+u)^4 ))du−∫((u+1−1)/((1+u)^4 ))du = 2∫(1/((1+u)^4 ))du−∫(1/((1+u)^3 ))du ⇒ Q=−(2/(3(1+u)^3 ))+(1/(2(1+u)^2 ))+C ∴∵ Q=−(2/(3(1+sinx)^3 ))+(1/(2(1+sinx)^2 ))+C.. .............Le puissant............
$${Q}=\int\frac{{sec}^{\mathrm{2}} {x}}{\left({secx}+{tanx}\right)^{\mathrm{5}} }{dx}\:=\:\int\frac{{sec}^{\mathrm{2}} {x}}{\left(\frac{\mathrm{1}}{{cosx}}+\frac{{sinx}}{{cosx}}\right)^{\mathrm{5}} }{dx} \\ $$$$=\int\frac{{cos}^{\mathrm{3}} {x}}{\left(\mathrm{1}+{sinx}\right)^{\mathrm{5}} }{dx}\:=\:\int\frac{\left(\mathrm{1}−{sinx}\right)\left(\mathrm{1}+{sinx}\right){cosx}}{\left(\mathrm{1}+{sinx}\right)^{\mathrm{5}} }{dx} \\ $$$$=\int\frac{\mathrm{1}−{sinx}}{\left(\mathrm{1}+{sinx}\right)^{\mathrm{4}} }{cosdx}\:;\:{u}={sinx}\rightarrow{du}={cosxdx} \\ $$$$\Rightarrow\:{Q}=\int\frac{\mathrm{1}−{u}}{\left(\mathrm{1}+{u}\right)^{\mathrm{4}} }{du}\:=\:\int\frac{\mathrm{1}}{\left(\mathrm{1}+{u}\right)^{\mathrm{4}} }{du}−\int\frac{{u}+\mathrm{1}−\mathrm{1}}{\left(\mathrm{1}+{u}\right)^{\mathrm{4}} }{du} \\ $$$$=\:\mathrm{2}\int\frac{\mathrm{1}}{\left(\mathrm{1}+{u}\right)^{\mathrm{4}} }{du}−\int\frac{\mathrm{1}}{\left(\mathrm{1}+{u}\right)^{\mathrm{3}} }{du} \\ $$$$\Rightarrow\:{Q}=−\frac{\mathrm{2}}{\mathrm{3}\left(\mathrm{1}+{u}\right)^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{u}\right)^{\mathrm{2}} }+{C} \\ $$$$\:\:\:\:\therefore\because\:\:{Q}=−\frac{\mathrm{2}}{\mathrm{3}\left(\mathrm{1}+{sinx}\right)^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{sinx}\right)^{\mathrm{2}} }+{C}.. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:………….\mathscr{L}{e}\:{puissant}………… \\ $$
Commented by cortano last updated on 16/Oct/21
yes
$${yes} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *