Question Number 156924 by cortano last updated on 17/Oct/21
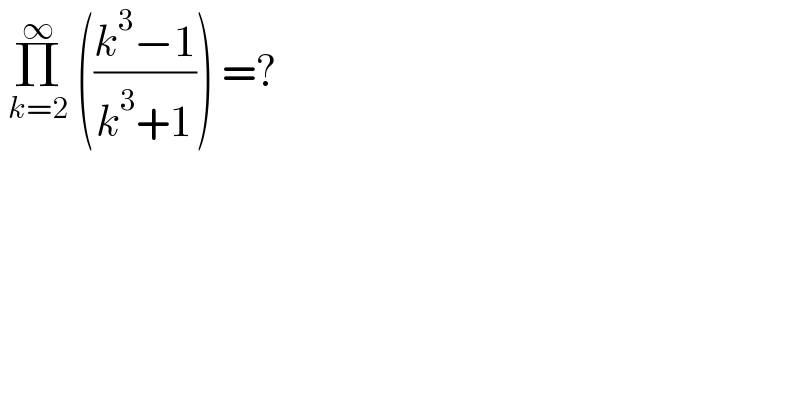
$$\:\underset{{k}=\mathrm{2}} {\overset{\infty} {\prod}}\:\left(\frac{{k}^{\mathrm{3}} −\mathrm{1}}{{k}^{\mathrm{3}} +\mathrm{1}}\right)\:=? \\ $$
Answered by puissant last updated on 17/Oct/21

$${P}=\underset{{k}=\mathrm{2}} {\overset{\infty} {\prod}}\left(\frac{{k}^{\mathrm{3}} −\mathrm{1}}{{k}^{\mathrm{3}} +\mathrm{1}}\right)\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\underset{{k}=\mathrm{2}} {\overset{{n}} {\prod}}\left(\frac{{k}^{\mathrm{3}} −\mathrm{1}}{{k}^{\mathrm{3}} +\mathrm{1}}\right) \\ $$$$=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\underset{{k}=\mathrm{2}} {\overset{{n}} {\prod}}\left(\frac{\left({k}−\mathrm{1}\right)\left({k}^{\mathrm{2}} +{k}+\mathrm{1}\right)}{\left({k}+\mathrm{1}\right)\left({k}^{\mathrm{2}} −{k}+\mathrm{1}\right)}\right)\:\underset{{n}\rightarrow\infty} {=\mathrm{lim}\:\underset{{k}=\mathrm{2}} {\overset{{n}} {\prod}}\left(\frac{{k}−\mathrm{1}}{{k}+\mathrm{1}}\right)×\mathrm{lim}\:\underset{{k}=\mathrm{2}} {\overset{{n}} {\prod}}\left(\frac{{k}^{\mathrm{2}} +{k}+\mathrm{1}}{{k}^{\mathrm{2}} −{k}+\mathrm{1}}\right)} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{\frac{\mathrm{1}}{\mathrm{3}}\bullet\frac{\mathrm{2}}{\mathrm{4}}\bullet\frac{\mathrm{3}}{\mathrm{5}}\bullet…\bullet\frac{{n}−\mathrm{2}}{{n}}\bullet\frac{{n}−\mathrm{1}}{{n}+\mathrm{1}}\right\}×\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{\frac{\mathrm{7}}{\mathrm{3}}\bullet\frac{\mathrm{13}}{\mathrm{7}}\bullet\frac{\mathrm{21}}{\mathrm{13}}\bullet…\bullet\frac{{n}^{\mathrm{2}} +{n}+\mathrm{1}}{{n}^{\mathrm{2}} −{n}+\mathrm{1}}\right\} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{\frac{\mathrm{2}}{{n}\left({n}+\mathrm{1}\right)}\right\}×\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{\frac{{n}^{\mathrm{2}} +{n}+\mathrm{1}}{\mathrm{3}}\right\}=\:\frac{\mathrm{2}}{\mathrm{3}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{\frac{{n}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)}{{n}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)}\right\}=\frac{\mathrm{2}}{\mathrm{3}}.. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\therefore\because\:{P}\:=\:\underset{{k}=\mathrm{2}} {\overset{\infty} {\prod}}\left(\frac{{k}^{\mathrm{3}} −\mathrm{1}}{{k}^{\mathrm{3}} +\mathrm{1}}\right)=\frac{\mathrm{2}}{\mathrm{3}}… \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:………………….\mathscr{L}{e}\:{puissant}……………… \\ $$
Commented by mnjuly1970 last updated on 17/Oct/21
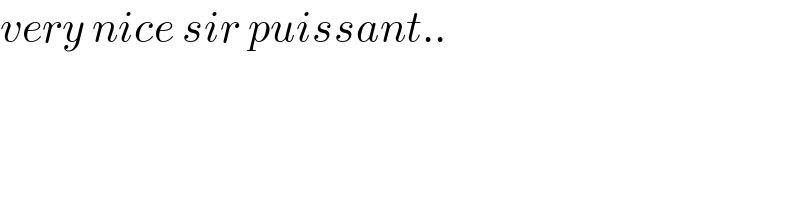
$${very}\:{nice}\:{sir}\:{puissant}.. \\ $$
Commented by puissant last updated on 17/Oct/21
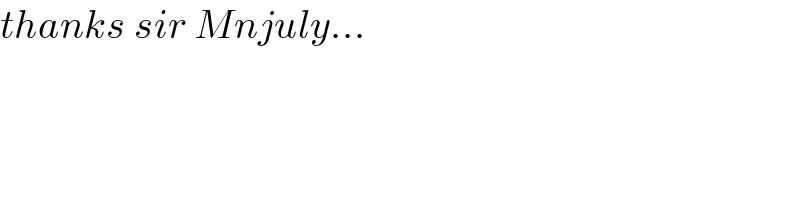
$${thanks}\:{sir}\:{Mnjuly}… \\ $$
Commented by Tawa11 last updated on 17/Oct/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
Commented by cortano last updated on 18/Oct/21

$${yes}\:\:{gave}\:{kudos} \\ $$
