Question Number 91421 by M±th+et+s last updated on 30/Apr/20
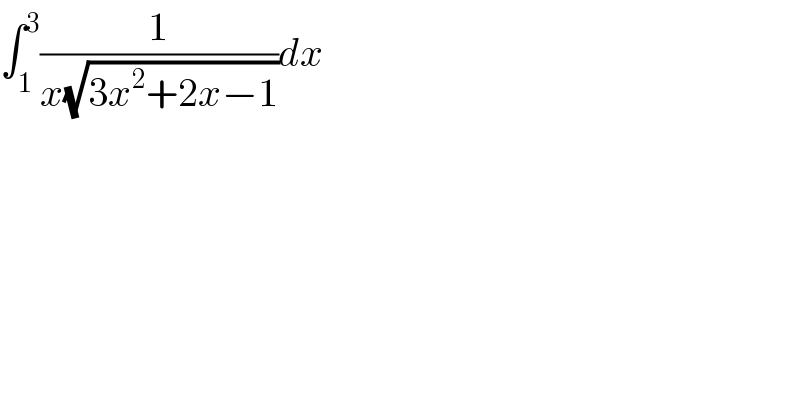
$$\int_{\mathrm{1}} ^{\mathrm{3}} \frac{\mathrm{1}}{{x}\sqrt{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{1}}}{dx} \\ $$
Commented by abdomathmax last updated on 30/Apr/20

$${I}\:=\int_{\mathrm{1}} ^{\mathrm{3}} \:\:\frac{{dx}}{{x}\sqrt{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{1}}} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} \:+\mathrm{2}{x}−\mathrm{1}=\mathrm{0}\rightarrow\:\Delta^{'} =\mathrm{1}+\mathrm{3}\:=\mathrm{4}\:\Rightarrow{x}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${x}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{2}}{\mathrm{3}}\:=−\mathrm{1}\:\Rightarrow{I}\:=\int_{\mathrm{1}} ^{\mathrm{3}} \:\frac{{dx}}{{x}\sqrt{\mathrm{3}\left({x}−\frac{\mathrm{1}}{\mathrm{3}}\right)\left({x}+\mathrm{1}\right)}} \\ $$$$=\:\int_{\mathrm{1}} ^{\mathrm{3}} \:\frac{{dx}}{{x}\sqrt{\left(\mathrm{3}{x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)}}\:=\int_{\mathrm{1}} ^{\mathrm{3}} \:\frac{{dx}}{{x}\sqrt{{x}+\mathrm{1}}\sqrt{\mathrm{3}{x}−\mathrm{1}}} \\ $$$${we}\:{do}\:{the}\:{changement}\:\sqrt{{x}+\mathrm{1}}={t}\:\Rightarrow{x}+\mathrm{1}\:={t}^{\mathrm{2}} \:\Rightarrow \\ $$$${I}\:=\int_{\sqrt{\mathrm{2}}} ^{\mathrm{2}} \:\:\frac{\mathrm{2}{tdt}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\mathrm{3}\left({t}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{1}}} \\ $$$$=\int_{\sqrt{\mathrm{2}}} ^{\mathrm{2}} \:\:\frac{\mathrm{2}{t}\:{dt}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}}}\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\int_{\sqrt{\mathrm{2}}} ^{\mathrm{2}} \:\frac{{tdt}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{{t}^{\mathrm{2}} −\frac{\mathrm{4}}{\mathrm{3}}}} \\ $$$$=_{{t}\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:{ch}\left({u}\right)\rightarrow{u}={argch}\left(\frac{{t}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)} \:\:\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\int_{{argch}\left(\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}\right)} ^{{argch}\left(\sqrt{\mathrm{3}}\right)} \:\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} ×\frac{{chu}\:{shu}}{\left(\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}{ch}^{\mathrm{2}} {u}−\mathrm{1}\right)\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:{shu}}{du} \\ $$$$=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}\:\int_{{argch}\left(\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}\right)} ^{{argch}\left(\sqrt{\mathrm{3}}\right)} \:\frac{{shu}}{\left(\mathrm{4}{ch}^{\mathrm{2}} {u}−\sqrt{\mathrm{3}}\right)}{du} \\ $$$$=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}\:\int_{{argch}\left(\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}\right)} ^{{argch}\left(\sqrt{\mathrm{3}}\right)} \:\:\frac{{shu}}{\left(\mathrm{4}×\frac{\mathrm{1}+{ch}\left(\mathrm{2}{u}\right)}{\mathrm{2}}−\sqrt{\mathrm{3}}\right)}{du} \\ $$$$=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}\:\int_{{argch}\left(\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}\right)} ^{{argch}\left(\sqrt{\mathrm{3}}\right)} \:\:\:\frac{{shu}}{\left(\mathrm{2}{ch}\left(\mathrm{2}{u}\right)+\mathrm{2}−\sqrt{\mathrm{3}}\right)}{du} \\ $$$$=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}\:\int_{{argch}\left(\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}\right)} ^{{argch}\left(\sqrt{\mathrm{3}}\right)} \:\:\frac{\frac{{e}^{{u}} −{e}^{−{u}} }{\mathrm{2}}}{{e}^{\mathrm{2}{u}} \:+{e}^{−\mathrm{2}{u}} \:+\mathrm{2}−\sqrt{\mathrm{3}}}{du} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\int_{\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}+\sqrt{\frac{\mathrm{6}}{\mathrm{4}}−\mathrm{1}}} ^{\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}} \:\:\:\:\frac{{z}−{z}^{−\mathrm{1}} }{{z}^{\mathrm{2}} \:+{z}^{−\mathrm{2}} \:+\mathrm{2}−\sqrt{\mathrm{3}}}\:\frac{{dz}}{{z}}\:\:\:\left({z}={e}^{{u}} \right) \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\int_{\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} ^{\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}} \:\:\:\:\:\frac{{z}^{\mathrm{2}} −\mathrm{1}}{{z}^{\mathrm{4}} \:+\mathrm{1}+\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){z}^{\mathrm{2}} }{dz} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\int_{\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} ^{\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}} \:\:\:\:\frac{{z}^{\mathrm{2}} −\mathrm{1}}{{z}^{\mathrm{4}} \:+\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){z}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:{let}\:{ddcompose} \\ $$$${F}\left({z}\right)\:=\frac{{z}^{\mathrm{2}} −\mathrm{1}}{{z}^{\mathrm{4}} \:+\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){z}^{\mathrm{2}} +\mathrm{1}}\:…{be}\:{continued}… \\ $$$$ \\ $$$$ \\ $$
Commented by jagoll last updated on 30/Apr/20
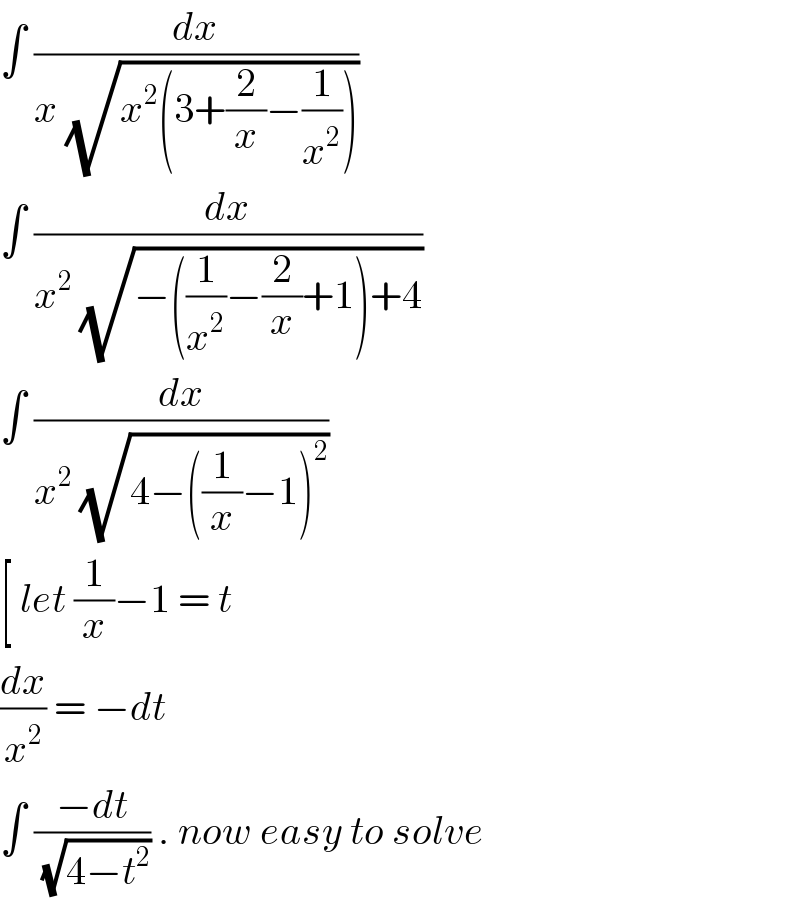
$$\int\:\frac{{dx}}{{x}\:\sqrt{{x}^{\mathrm{2}} \left(\mathrm{3}+\frac{\mathrm{2}}{{x}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}} \\ $$$$\int\:\frac{{dx}}{{x}^{\mathrm{2}} \:\sqrt{−\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{2}}{{x}}+\mathrm{1}\right)+\mathrm{4}}} \\ $$$$\int\:\frac{{dx}}{{x}^{\mathrm{2}} \:\sqrt{\mathrm{4}−\left(\frac{\mathrm{1}}{{x}}−\mathrm{1}\right)^{\mathrm{2}} }} \\ $$$$\left[\:{let}\:\frac{\mathrm{1}}{{x}}−\mathrm{1}\:=\:{t}\:\right. \\ $$$$\frac{{dx}}{{x}^{\mathrm{2}} }\:=\:−{dt}\: \\ $$$$\int\:\frac{−{dt}}{\:\sqrt{\mathrm{4}−{t}^{\mathrm{2}} }}\:.\:{now}\:{easy}\:{to}\:{solve} \\ $$
Answered by jagoll last updated on 30/Apr/20

Commented by M±th+et+s last updated on 30/Apr/20
$${nice}\:{work}\:{thanks} \\ $$
Answered by MJS last updated on 01/May/20

$${x}^{\mathrm{2}} \left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{1}\right)={x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)\left(\mathrm{3}{x}−\mathrm{1}\right) \\ $$$$\mathrm{let}\:{x}=\frac{\mathrm{1}}{{at}+{b}} \\ $$$$−\frac{\left({at}+{b}−\mathrm{3}\right)\left({at}+{b}+\mathrm{1}\right)}{\left({at}+{b}\right)^{\mathrm{4}} } \\ $$$${at}+{b}−\mathrm{3}={t}−{c}\:\Leftrightarrow\:\left({a}−\mathrm{1}\right){t}+{b}+{c}−\mathrm{3}=\mathrm{0} \\ $$$${at}+{b}+\mathrm{1}={t}+{c}\:\Leftrightarrow\:\left({a}−\mathrm{1}\right){t}+{b}−{c}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:{a}=\mathrm{1} \\ $$$${b}+{c}−\mathrm{3}=\mathrm{0}\wedge{b}−{c}+\mathrm{1}=\mathrm{0}\:\Rightarrow\:{b}=\mathrm{1}\wedge{k}=\mathrm{2} \\ $$$$−\frac{\left({t}−\mathrm{2}\right)\left({t}+\mathrm{2}\right)}{\left({t}+\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$\mathrm{let}\:{t}=\mathrm{2}{u} \\ $$$$−\frac{\mathrm{4}\left({u}−\mathrm{1}\right)\left({u}+\mathrm{1}\right)}{\left(\mathrm{2}{u}+\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$\Rightarrow \\ $$$$\mathrm{let}\:{x}=\frac{\mathrm{1}}{\mathrm{2sin}\:{u}+\mathrm{1}}\:\Leftrightarrow\:{u}=\mathrm{arcsin}\:\frac{{x}−\mathrm{1}}{\mathrm{2}{x}}\:\rightarrow\:{dx}={x}\sqrt{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{1}}{du} \\ $$$$\int\frac{{dx}}{{x}\sqrt{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{1}}}=\int{du}={u}=\mathrm{arcsin}\:\frac{{x}−\mathrm{1}}{\mathrm{2}{x}}\:+{C} \\ $$
