Question Number 156991 by MathSh last updated on 18/Oct/21
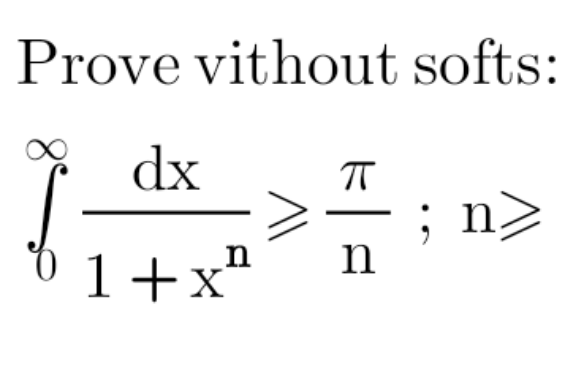
Answered by mindispower last updated on 18/Oct/21
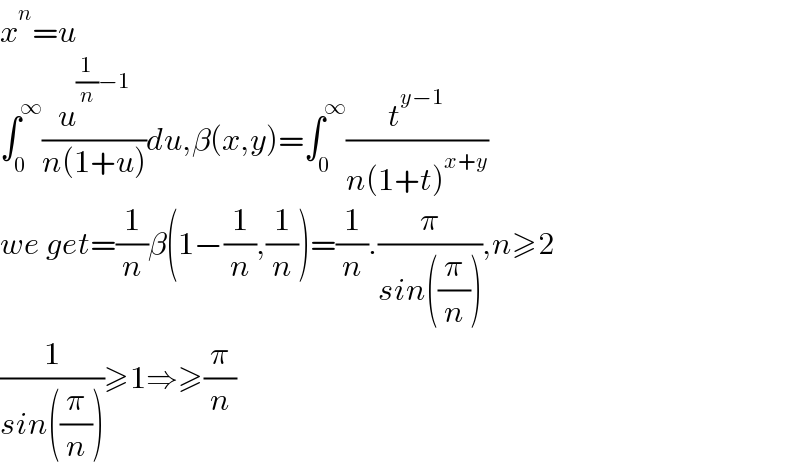
$${x}^{{n}} ={u} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} }{{n}\left(\mathrm{1}+{u}\right)}{du},\beta\left({x},{y}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{y}−\mathrm{1}} }{{n}\left(\mathrm{1}+{t}\right)^{{x}+{y}} } \\ $$$${we}\:{get}=\frac{\mathrm{1}}{{n}}\beta\left(\mathrm{1}−\frac{\mathrm{1}}{{n}},\frac{\mathrm{1}}{{n}}\right)=\frac{\mathrm{1}}{{n}}.\frac{\pi}{{sin}\left(\frac{\pi}{{n}}\right)},{n}\geqslant\mathrm{2} \\ $$$$\frac{\mathrm{1}}{{sin}\left(\frac{\pi}{{n}}\right)}\geqslant\mathrm{1}\Rightarrow\geqslant\frac{\pi}{{n}} \\ $$
Commented by MathSh last updated on 18/Oct/21
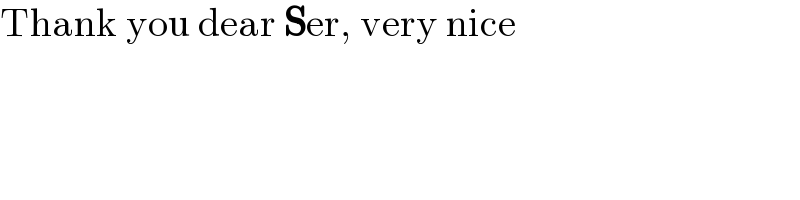
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{very}\:\mathrm{nice} \\ $$
Commented by mindispower last updated on 19/Oct/21

$${withe}\:{plesur} \\ $$
