Menu Close

f-z-e-1-z-f-1-z-pi-z-sin-piz-f-z-z-2-z-1-2-f-z-0-z-

Tinku Tara 0 Comments
Pin




Question Number 2344 by 123456 last updated on 17/Nov/15
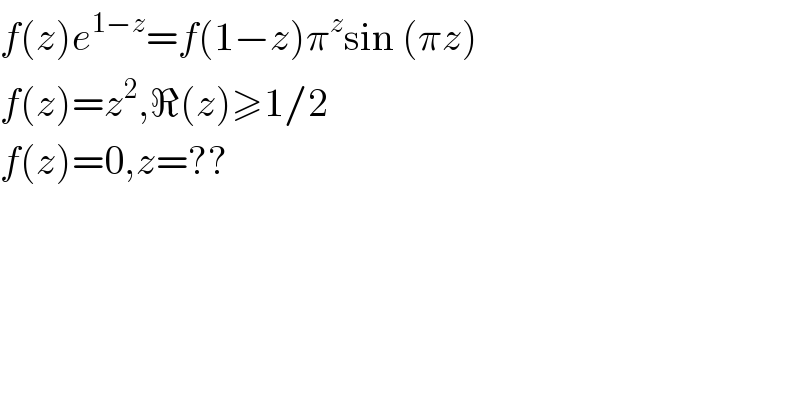
f(z)e^(1−z) =f(1−z)π^z sin (πz) f(z)=z^2 ,ℜ(z)≥1/2 f(z)=0,z=??
$${f}\left({z}\right){e}^{\mathrm{1}−{z}} ={f}\left(\mathrm{1}−{z}\right)\pi^{{z}} \mathrm{sin}\:\left(\pi{z}\right) \\ $$$${f}\left({z}\right)={z}^{\mathrm{2}} ,\Re\left({z}\right)\geqslant\mathrm{1}/\mathrm{2} \\ $$$${f}\left({z}\right)=\mathrm{0},{z}=?? \\ $$
Commented by Yozzi last updated on 17/Nov/15
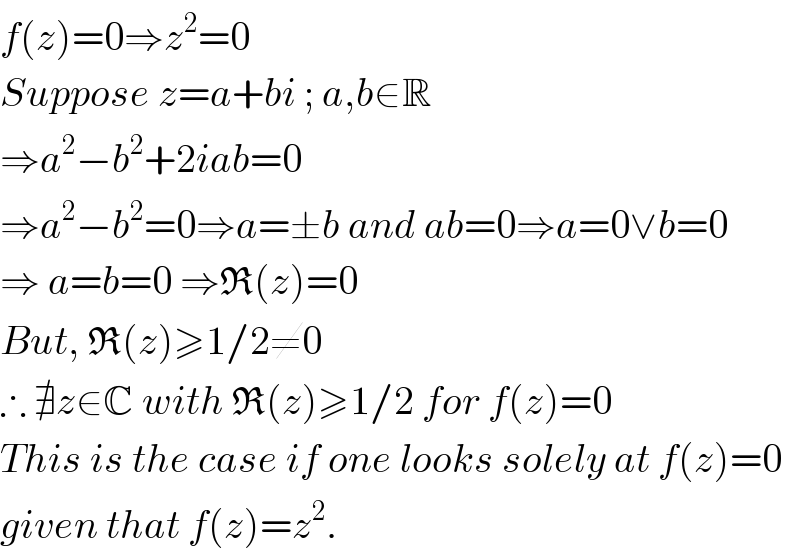
f(z)=0⇒z^2 =0 Suppose z=a+bi ; a,b∈R ⇒a^2 −b^2 +2iab=0 ⇒a^2 −b^2 =0⇒a=±b and ab=0⇒a=0∨b=0 ⇒ a=b=0 ⇒R(z)=0 But, R(z)≥1/2≠0 ∴ ∄z∈C with R(z)≥1/2 for f(z)=0 This is the case if one looks solely at f(z)=0 given that f(z)=z^2 .
$${f}\left({z}\right)=\mathrm{0}\Rightarrow{z}^{\mathrm{2}} =\mathrm{0} \\ $$$${Suppose}\:{z}={a}+{bi}\:;\:{a},{b}\in\mathbb{R} \\ $$$$\Rightarrow{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +\mathrm{2}{iab}=\mathrm{0} \\ $$$$\Rightarrow{a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{0}\Rightarrow{a}=\pm{b}\:{and}\:{ab}=\mathrm{0}\Rightarrow{a}=\mathrm{0}\vee{b}=\mathrm{0} \\ $$$$\Rightarrow\:{a}={b}=\mathrm{0}\:\Rightarrow\mathfrak{R}\left({z}\right)=\mathrm{0} \\ $$$${But},\:\mathfrak{R}\left({z}\right)\geqslant\mathrm{1}/\mathrm{2}\neq\mathrm{0} \\ $$$$\therefore\:\nexists{z}\in\mathbb{C}\:{with}\:\mathfrak{R}\left({z}\right)\geqslant\mathrm{1}/\mathrm{2}\:{for}\:{f}\left({z}\right)=\mathrm{0} \\ $$$${This}\:{is}\:{the}\:{case}\:{if}\:{one}\:{looks}\:{solely}\:{at}\:{f}\left({z}\right)=\mathrm{0} \\ $$$${given}\:{that}\:{f}\left({z}\right)={z}^{\mathrm{2}} . \\ $$
Commented by Yozzi last updated on 17/Nov/15
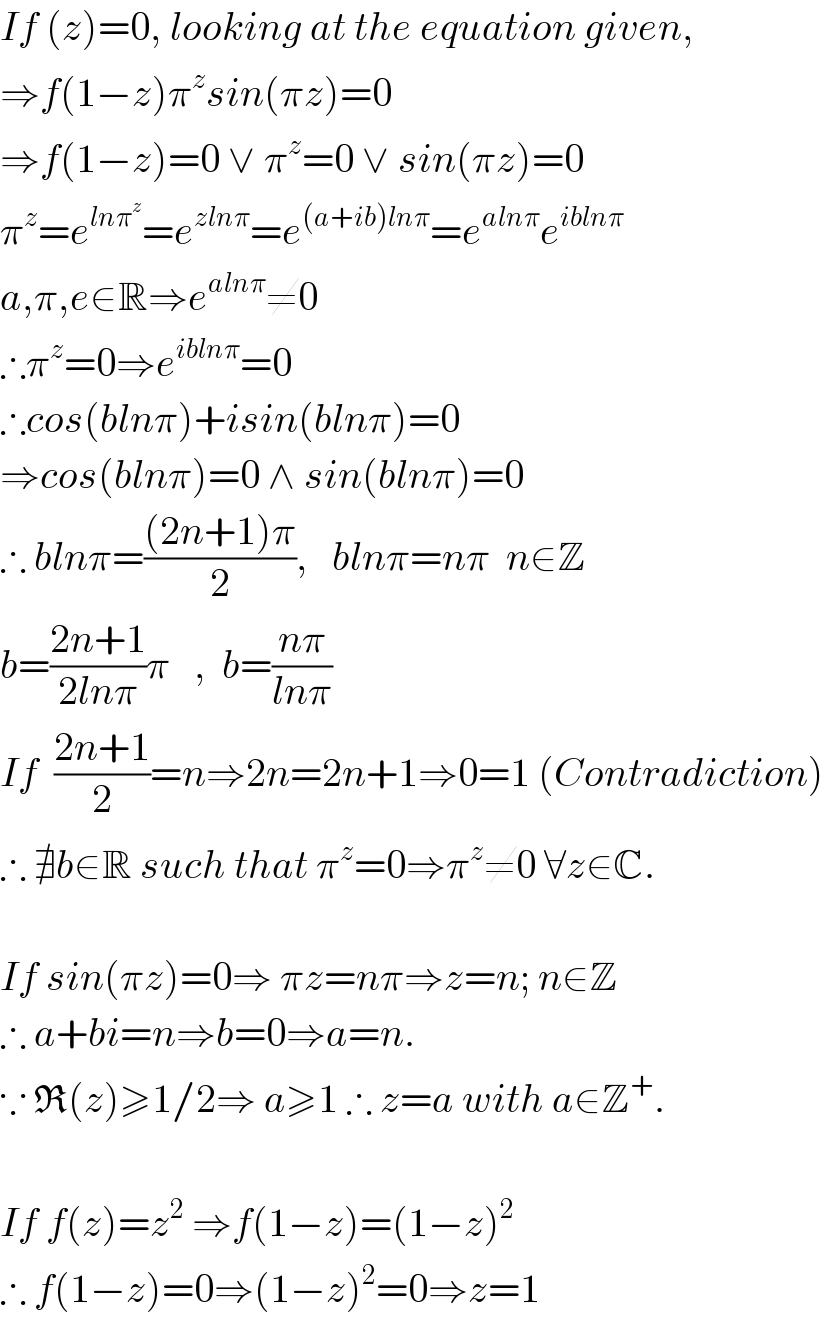
If (z)=0, looking at the equation given, ⇒f(1−z)π^z sin(πz)=0 ⇒f(1−z)=0 ∨ π^z =0 ∨ sin(πz)=0 π^z =e^(lnπ^z ) =e^(zlnπ) =e^((a+ib)lnπ) =e^(alnπ) e^(iblnπ) a,π,e∈R⇒e^(alnπ) ≠0 ∴π^z =0⇒e^(iblnπ) =0 ∴cos(blnπ)+isin(blnπ)=0 ⇒cos(blnπ)=0 ∧ sin(blnπ)=0 ∴ blnπ=(((2n+1)π)/2), blnπ=nπ n∈Z b=((2n+1)/(2lnπ))π , b=((nπ)/(lnπ)) If ((2n+1)/2)=n⇒2n=2n+1⇒0=1 (Contradiction) ∴ ∄b∈R such that π^z =0⇒π^z ≠0 ∀z∈C. If sin(πz)=0⇒ πz=nπ⇒z=n; n∈Z ∴ a+bi=n⇒b=0⇒a=n. ∵ R(z)≥1/2⇒ a≥1 ∴ z=a with a∈Z^+ . If f(z)=z^2 ⇒f(1−z)=(1−z)^2 ∴ f(1−z)=0⇒(1−z)^2 =0⇒z=1
$${If}\:\left({z}\right)=\mathrm{0},\:{looking}\:{at}\:{the}\:{equation}\:{given}, \\ $$$$\Rightarrow{f}\left(\mathrm{1}−{z}\right)\pi^{{z}} {sin}\left(\pi{z}\right)=\mathrm{0} \\ $$$$\Rightarrow{f}\left(\mathrm{1}−{z}\right)=\mathrm{0}\:\vee\:\pi^{{z}} =\mathrm{0}\:\vee\:{sin}\left(\pi{z}\right)=\mathrm{0} \\ $$$$\pi^{{z}} ={e}^{{ln}\pi^{{z}} } ={e}^{{zln}\pi} ={e}^{\left({a}+{ib}\right){ln}\pi} ={e}^{{aln}\pi} {e}^{{ibln}\pi} \\ $$$${a},\pi,{e}\in\mathbb{R}\Rightarrow{e}^{{aln}\pi} \neq\mathrm{0} \\ $$$$\therefore\pi^{{z}} =\mathrm{0}\Rightarrow{e}^{{ibln}\pi} =\mathrm{0} \\ $$$$\therefore{cos}\left({bln}\pi\right)+{isin}\left({bln}\pi\right)=\mathrm{0} \\ $$$$\Rightarrow{cos}\left({bln}\pi\right)=\mathrm{0}\:\wedge\:{sin}\left({bln}\pi\right)=\mathrm{0} \\ $$$$\therefore\:{bln}\pi=\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi}{\mathrm{2}},\:\:\:{bln}\pi={n}\pi\:\:{n}\in\mathbb{Z} \\ $$$${b}=\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}{ln}\pi}\pi\:\:\:,\:\:{b}=\frac{{n}\pi}{{ln}\pi} \\ $$$${If}\:\:\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}={n}\Rightarrow\mathrm{2}{n}=\mathrm{2}{n}+\mathrm{1}\Rightarrow\mathrm{0}=\mathrm{1}\:\left({Contradiction}\right) \\ $$$$\therefore\:\nexists{b}\in\mathbb{R}\:{such}\:{that}\:\pi^{{z}} =\mathrm{0}\Rightarrow\pi^{{z}} \neq\mathrm{0}\:\forall{z}\in\mathbb{C}. \\ $$$$ \\ $$$${If}\:{sin}\left(\pi{z}\right)=\mathrm{0}\Rightarrow\:\pi{z}={n}\pi\Rightarrow{z}={n};\:{n}\in\mathbb{Z} \\ $$$$\therefore\:{a}+{bi}={n}\Rightarrow{b}=\mathrm{0}\Rightarrow{a}={n}. \\ $$$$\because\:\mathfrak{R}\left({z}\right)\geqslant\mathrm{1}/\mathrm{2}\Rightarrow\:{a}\geqslant\mathrm{1}\:\therefore\:{z}={a}\:{with}\:{a}\in\mathbb{Z}^{+} . \\ $$$$ \\ $$$${If}\:{f}\left({z}\right)={z}^{\mathrm{2}} \:\Rightarrow{f}\left(\mathrm{1}−{z}\right)=\left(\mathrm{1}−{z}\right)^{\mathrm{2}} \\ $$$$\therefore\:{f}\left(\mathrm{1}−{z}\right)=\mathrm{0}\Rightarrow\left(\mathrm{1}−{z}\right)^{\mathrm{2}} =\mathrm{0}\Rightarrow{z}=\mathrm{1} \\ $$
Commented by RasheedAhmad last updated on 17/Nov/15
Excellent!
$$\mathcal{E}{xcellent}! \\ $$
Commented by RasheedAhmad last updated on 17/Nov/15
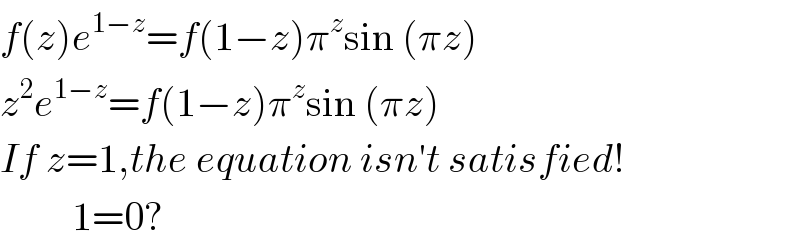
f(z)e^(1−z) =f(1−z)π^z sin (πz) z^2 e^(1−z) =f(1−z)π^z sin (πz) If z=1,the equation isn′t satisfied! 1=0?
$${f}\left({z}\right){e}^{\mathrm{1}−{z}} ={f}\left(\mathrm{1}−{z}\right)\pi^{{z}} \mathrm{sin}\:\left(\pi{z}\right) \\ $$$${z}^{\mathrm{2}} {e}^{\mathrm{1}−{z}} ={f}\left(\mathrm{1}−{z}\right)\pi^{{z}} \mathrm{sin}\:\left(\pi{z}\right) \\ $$$${If}\:{z}=\mathrm{1},{the}\:{equation}\:{isn}'{t}\:{satisfied}! \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{1}=\mathrm{0}? \\ $$
Commented by Yozzi last updated on 17/Nov/15
Yup, certainly. It′s false for z=a, a∈Z^+ too. Given the condition R(z)≥1/2 for f(z)=0, there are no solutions. Perhaps one should look at e^(1−z) =0.
$${Yup},\:{certainly}.\:{It}'{s}\:{false}\:{for}\:{z}={a},\:{a}\in\mathbb{Z}^{+} \:{too}. \\ $$$${Given}\:{the}\:{condition}\:\mathfrak{R}\left({z}\right)\geqslant\mathrm{1}/\mathrm{2} \\ $$$${for}\:{f}\left({z}\right)=\mathrm{0},\:{there}\:{are}\:{no}\:{solutions}. \\ $$$${Perhaps}\:{one}\:{should}\:{look}\:{at}\:{e}^{\mathrm{1}−{z}} =\mathrm{0}. \\ $$
Commented by Yozzi last updated on 17/Nov/15
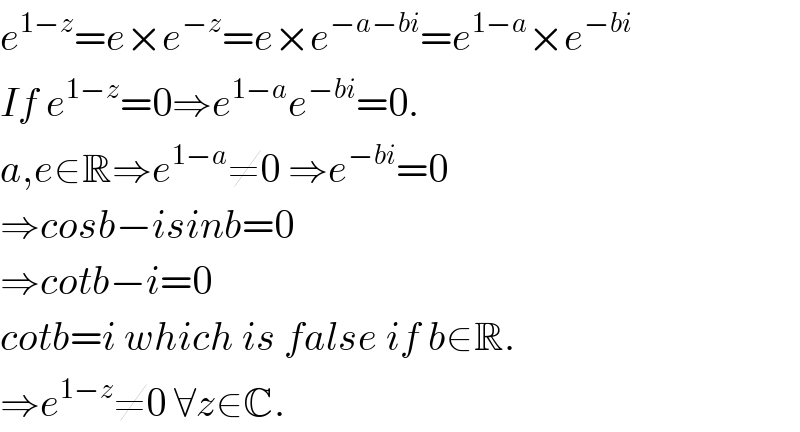
e^(1−z) =e×e^(−z) =e×e^(−a−bi) =e^(1−a) ×e^(−bi) If e^(1−z) =0⇒e^(1−a) e^(−bi) =0. a,e∈R⇒e^(1−a) ≠0 ⇒e^(−bi) =0 ⇒cosb−isinb=0 ⇒cotb−i=0 cotb=i which is false if b∈R. ⇒e^(1−z) ≠0 ∀z∈C.
$${e}^{\mathrm{1}−{z}} ={e}×{e}^{−{z}} ={e}×{e}^{−{a}−{bi}} ={e}^{\mathrm{1}−{a}} ×{e}^{−{bi}} \\ $$$${If}\:{e}^{\mathrm{1}−{z}} =\mathrm{0}\Rightarrow{e}^{\mathrm{1}−{a}} {e}^{−{bi}} =\mathrm{0}. \\ $$$${a},{e}\in\mathbb{R}\Rightarrow{e}^{\mathrm{1}−{a}} \neq\mathrm{0}\:\Rightarrow{e}^{−{bi}} =\mathrm{0} \\ $$$$\Rightarrow{cosb}−{isinb}=\mathrm{0} \\ $$$$\Rightarrow{cotb}−{i}=\mathrm{0} \\ $$$${cotb}={i}\:{which}\:{is}\:{false}\:{if}\:{b}\in\mathbb{R}. \\ $$$$\Rightarrow{e}^{\mathrm{1}−{z}} \neq\mathrm{0}\:\forall{z}\in\mathbb{C}. \\ $$
Commented by prakash jain last updated on 17/Nov/15
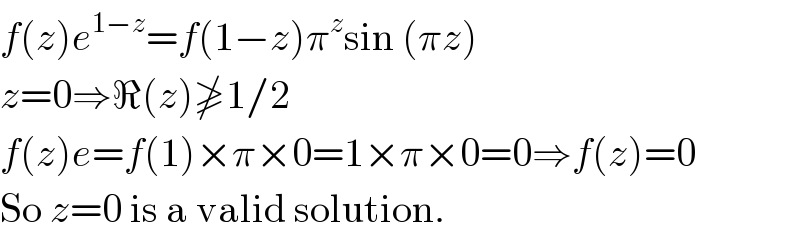
f(z)e^(1−z) =f(1−z)π^z sin (πz) z=0⇒ℜ(z)≱1/2 f(z)e=f(1)×π×0=1×π×0=0⇒f(z)=0 So z=0 is a valid solution.
$${f}\left({z}\right){e}^{\mathrm{1}−{z}} ={f}\left(\mathrm{1}−{z}\right)\pi^{{z}} \mathrm{sin}\:\left(\pi{z}\right) \\ $$$${z}=\mathrm{0}\Rightarrow\Re\left({z}\right)\ngeqslant\mathrm{1}/\mathrm{2} \\ $$$${f}\left({z}\right){e}={f}\left(\mathrm{1}\right)×\pi×\mathrm{0}=\mathrm{1}×\pi×\mathrm{0}=\mathrm{0}\Rightarrow{f}\left({z}\right)=\mathrm{0} \\ $$$$\mathrm{So}\:{z}=\mathrm{0}\:\mathrm{is}\:\mathrm{a}\:\mathrm{valid}\:\mathrm{solution}. \\ $$
Commented by Yozzi last updated on 17/Nov/15
Yes.
$${Yes}. \\ $$
Answered by prakash jain last updated on 17/Nov/15
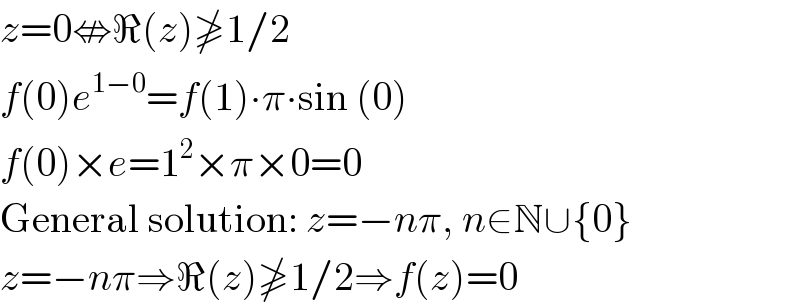
z=0⇎ℜ(z)≱1/2 f(0)e^(1−0) =f(1)∙π∙sin (0) f(0)×e=1^2 ×π×0=0 General solution: z=−nπ, n∈N∪{0} z=−nπ⇒ℜ(z)≱1/2⇒f(z)=0
$${z}=\mathrm{0}\nLeftrightarrow\Re\left({z}\right)\ngeqslant\mathrm{1}/\mathrm{2} \\ $$$${f}\left(\mathrm{0}\right){e}^{\mathrm{1}−\mathrm{0}} ={f}\left(\mathrm{1}\right)\centerdot\pi\centerdot\mathrm{sin}\:\left(\mathrm{0}\right) \\ $$$${f}\left(\mathrm{0}\right)×{e}=\mathrm{1}^{\mathrm{2}} ×\pi×\mathrm{0}=\mathrm{0} \\ $$$$\mathrm{General}\:\mathrm{solution}:\:{z}=−{n}\pi,\:{n}\in\mathbb{N}\cup\left\{\mathrm{0}\right\} \\ $$$${z}=−{n}\pi\Rightarrow\Re\left({z}\right)\ngeqslant\mathrm{1}/\mathrm{2}\Rightarrow{f}\left({z}\right)=\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *