Menu Close

find-the-rsdius-of-convergence-for-theserie-n-0-x-n-2n-1-and-calculate-its-sum-s-x-find-the-value-of-n-0-1-2-n-2n-1-

Tinku Tara 0 Comments
Pin




Question Number 26192 by abdo imad last updated on 22/Dec/17
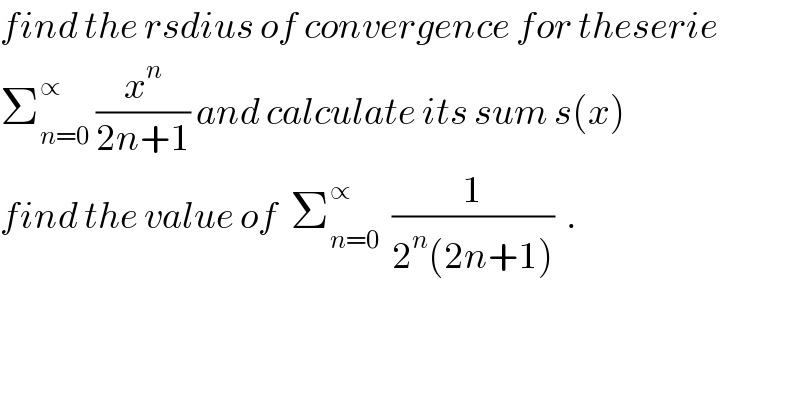
find the rsdius of convergence for theserie Σ_(n=0) ^∝ (x^n /(2n+1)) and calculate its sum s(x) find the value of Σ_(n=0) ^∝ (1/(2^n (2n+1))) .
$${find}\:{the}\:{rsdius}\:{of}\:{convergence}\:{for}\:{theserie} \\ $$$$\sum_{{n}=\mathrm{0}} ^{\propto} \:\frac{{x}^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:{and}\:{calculate}\:{its}\:{sum}\:{s}\left({x}\right) \\ $$$${find}\:{the}\:{value}\:{of}\:\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\:\frac{\mathrm{1}}{\mathrm{2}^{{n}} \left(\mathrm{2}{n}+\mathrm{1}\right)}\:\:. \\ $$
Commented by prakash jain last updated on 22/Dec/17
ratio test lim_(n→∞) ∣(x^(n+1) /(2n+1))∙((2n)/x^n )∣=∣x∣lim_(n→∞) ((2n)/(2n+1))=∣x∣ ∣x∣<1 ⇒series converges ∣x∣>1⇒series diverges ____ x=1 Σ_(n=0) ^∞ (1/(2n+1)) , we know it diverges radius of convergence ∣x∣<1
$${ratio}\:{test} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\mid\frac{{x}^{{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\centerdot\frac{\mathrm{2}{n}}{{x}^{{n}} }\mid=\mid{x}\mid\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2}{n}}{\mathrm{2}{n}+\mathrm{1}}=\mid{x}\mid \\ $$$$\mid{x}\mid<\mathrm{1}\:\Rightarrow\mathrm{series}\:\mathrm{converges} \\ $$$$\mid{x}\mid>\mathrm{1}\Rightarrow\mathrm{series}\:\mathrm{diverges} \\ $$$$\_\_\_\_ \\ $$$${x}=\mathrm{1} \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:,\:\mathrm{we}\:\mathrm{know}\:\mathrm{it}\:\mathrm{diverges} \\ $$$$\mathrm{radius}\:\mathrm{of}\:\mathrm{convergence}\:\mid{x}\mid<\mathrm{1} \\ $$
Commented by abdo imad last updated on 22/Dec/17
let put a_n (x) = ((x^n )/(2n+1 )) per x not0 /((a_(n+1) (x))/(a_n (x)))/=/ (x^(n+1) /(2n+3)) ((x^n /(2n+1)))^(−1) / =/((2n+1)/(2n+3))x/ = ((2n+1)/(2n+3))/x/ and lim_(n−>∝) / ((a_(n+1) (x))/a_(n(x)) )/= /x/⇒ if /x/<1 the serie is convergent if /x/>1 the serie diverge if x=1 also the serie diverge if x=−1 Σ_(n≥0) (((−1)^n )/(2n+1)) is convergent because its a alterne serie et S(x)= Σ_(n=0) ^(∝ ) (x^n /(2n+1)) the sum for /x/<1 case1 0<x<1 S(x) = Σ_(n=0) ^∝ ((((√x))^(2n) )/(2n+1)) = (1/( (√x))) Σ_(n=0) ^∝ ((((√x))^(2n+1) )/(2n+1)) = (1/( (√x))) ϕ((√x))with ϕ(t) = Σ_(n=0) ^∝ (t^(2n+1) /(2n+1)) and /t/<1 ∂ϕ/∂t = Σ_(n=0) ^∝ t^(2n) = (1/(1−t^2 )) ⇒ ϕ(t) =∫ (dt/(1−t^2 )) +λ =(1/2)ln/((1+t)/(1−t))/+λ λ=ϕ(0)=0⇒ S(x)= (1/(2(√x)))ln(((1+(√x))/(1−(√x))) ) case2 −1<x<0 S(x)= Σ_(n=0) ^(∝ ) (((−1)^n ((√(−x)))^(2n) )/(2n+1)) = (1/( (√(−x)))) Σ_(n=0) ^∝ (((−1)^n ((√(−x)))^(2n+1) )/(2n+1))= (1/( (√(−x))))ψ((√(−x))) with ψ(t)= Σ_(n=0) ^∝ (((−1)^n t^(2n+1) )/(2n+1)) and /t/<1 ∂ψ/∂t = Σ_(n=0) ^∝ (−1)^n t^(2n) = Σ_(n=0) ^∝ (−t^2 )^n = (1/(1+t^2 )) ⇒ ψ(t)= ∫ (dt/(1+t^2 )) +κ = arctant +κ k=ψ(0)=0⇒ S(x)= ((artan((√(−x))))/( (√(−x)))) . value of S= Σ_(n=0) ^∝ (1/(2^n (2n+1))) we have proved that Σ_(n=0) ^∝ (x^n /(2n+1)) =(1/(2(√x))) ln(((1+(√x))/(1−(√x)))) if 0x<1 we take x=(1/2)⇒ S= (1/(2(√(1/2))))ln( ((1+(√(1/2)))/(1−(√(1/2))))) =(1/( (√2))) ln(((1+(√2))/(−1+(√2))))
$${let}\:{put}\:\:{a}_{{n}} \left({x}\right)\:\:=\:\frac{{x}^{{n}} \:\:\:\:\:}{\mathrm{2}{n}+\mathrm{1}\:}\:\:\:\:{per}\:{x}\:{not}\mathrm{0} \\ $$$$/\frac{{a}_{{n}+\mathrm{1}} \left({x}\right)}{{a}_{{n}} \left({x}\right)}/=/\:\frac{{x}^{{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{3}}\:\left(\frac{{x}^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\right)^{−\mathrm{1}} /\:\:=/\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}{n}+\mathrm{3}}{x}/\:\:=\:\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}{n}+\mathrm{3}}/{x}/ \\ $$$${and}\:{lim}_{{n}−>\propto} \:\:/\:\frac{{a}_{{n}+\mathrm{1}} \left({x}\right)}{{a}_{{n}\left({x}\right)} }/=\:/{x}/\Rightarrow\:\:{if}\:\:/{x}/<\mathrm{1}\:{the}\:{serie}\:{is}\:{convergent} \\ $$$${if}\:/{x}/>\mathrm{1}\:{the}\:{serie}\:{diverge}\:\:{if}\:{x}=\mathrm{1}\:{also}\:{the}\:{serie}\:{diverge} \\ $$$${if}\:{x}=−\mathrm{1}\:\:\:\:\sum_{{n}\geqslant\mathrm{0}} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:{is}\:{convergent}\:{because}\:{its}\:{a}\:{alterne}\:{serie} \\ $$$${et}\:{S}\left({x}\right)=\:\:\sum_{{n}=\mathrm{0}} ^{\propto\:} \:\frac{{x}^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:{the}\:{sum}\:{for}\:/{x}/<\mathrm{1} \\ $$$${case}\mathrm{1}\:\:\:\:\mathrm{0}<{x}<\mathrm{1}\:\:\:\:\:{S}\left({x}\right)\:\:=\:\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\frac{\left(\sqrt{{x}}\right)^{\mathrm{2}{n}} }{\mathrm{2}{n}+\mathrm{1}}\:\:=\:\frac{\mathrm{1}}{\:\sqrt{{x}}}\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\frac{\left(\sqrt{{x}}\right)^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$$=\:\:\frac{\mathrm{1}}{\:\sqrt{{x}}}\:\varphi\left(\sqrt{{x}}\right){with}\:\:\varphi\left({t}\right)\:\:=\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\frac{{t}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\:\:\:{and}\:/{t}/<\mathrm{1} \\ $$$$\partial\varphi/\partial{t}\:\:=\:\:\sum_{{n}=\mathrm{0}} ^{\propto} \:{t}^{\mathrm{2}{n}} \:\:\:=\:\frac{\mathrm{1}}{\mathrm{1}−{t}^{\mathrm{2}} }\:\Rightarrow\:\:\varphi\left({t}\right)\:=\int\:\frac{{dt}}{\mathrm{1}−{t}^{\mathrm{2}} }\:+\lambda \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}/\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}/+\lambda\:\:\:\:\:\:\:\lambda=\varphi\left(\mathrm{0}\right)=\mathrm{0}\Rightarrow\:\:{S}\left({x}\right)=\:\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}{ln}\left(\frac{\mathrm{1}+\sqrt{{x}}}{\mathrm{1}−\sqrt{{x}}}\:\right) \\ $$$${case}\mathrm{2}\:\:\:\:\:\:−\mathrm{1}<{x}<\mathrm{0}\:\:\:\:\:{S}\left({x}\right)=\:\:\sum_{{n}=\mathrm{0}} ^{\propto\:} \:\frac{\left(−\mathrm{1}\right)^{{n}} \left(\sqrt{−{x}}\right)^{\mathrm{2}{n}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{−{x}}}\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} \left(\sqrt{−{x}}\right)^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}=\:\frac{\mathrm{1}}{\:\sqrt{−{x}}}\psi\left(\sqrt{−{x}}\right)\:\:\:{with} \\ $$$$\psi\left({t}\right)=\:\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\frac{\left(−\mathrm{1}\right)^{{n}} \:{t}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\:\:\:{and}\:\:/{t}/<\mathrm{1} \\ $$$$\partial\psi/\partial{t}\:=\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\left(−\mathrm{1}\right)^{{n}} \:{t}^{\mathrm{2}{n}} =\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\left(−{t}^{\mathrm{2}} \right)^{{n}} =\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\psi\left({t}\right)=\:\int\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\:+\kappa\:\:=\:\:{arctant}\:+\kappa\:\:\:\:\:\:\:{k}=\psi\left(\mathrm{0}\right)=\mathrm{0}\Rightarrow \\ $$$${S}\left({x}\right)=\:\frac{{artan}\left(\sqrt{−{x}}\right)}{\:\sqrt{−{x}}}\:\:. \\ $$$${value}\:{of}\:{S}=\:\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\:\:\frac{\mathrm{1}}{\mathrm{2}^{{n}} \left(\mathrm{2}{n}+\mathrm{1}\right)}\:\:\:{we}\:{have}\:{proved}\:{that}\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\:\frac{{x}^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}\:{ln}\left(\frac{\mathrm{1}+\sqrt{{x}}}{\mathrm{1}−\sqrt{{x}}}\right)\:{if}\:\mathrm{0}{x}<\mathrm{1} \\ $$$${we}\:{take}\:{x}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\:\:\:\:\:\:{S}=\:\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}}{ln}\left(\:\:\frac{\mathrm{1}+\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}}{\mathrm{1}−\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}}\right) \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{−\mathrm{1}+\sqrt{\mathrm{2}}}\right) \\ $$$$ \\ $$
Commented by prakash jain last updated on 22/Dec/17
Thanks

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *