Question Number 157324 by ZiYangLee last updated on 22/Oct/21
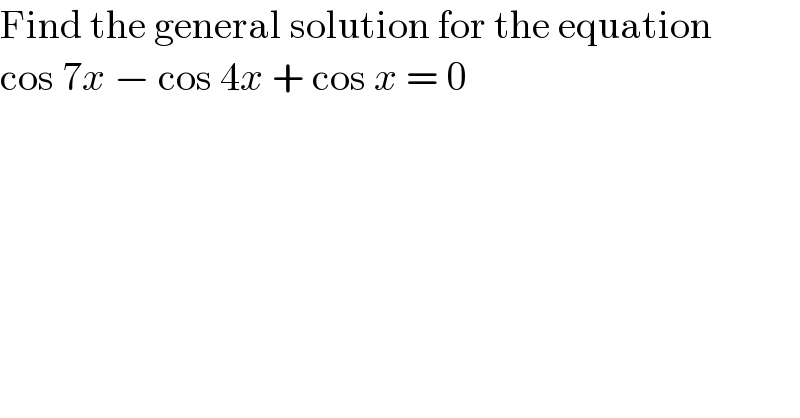
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{for}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{cos}\:\mathrm{7}{x}\:−\:\mathrm{cos}\:\mathrm{4}{x}\:+\:\mathrm{cos}\:{x}\:=\:\mathrm{0} \\ $$
Commented by cortano last updated on 22/Oct/21
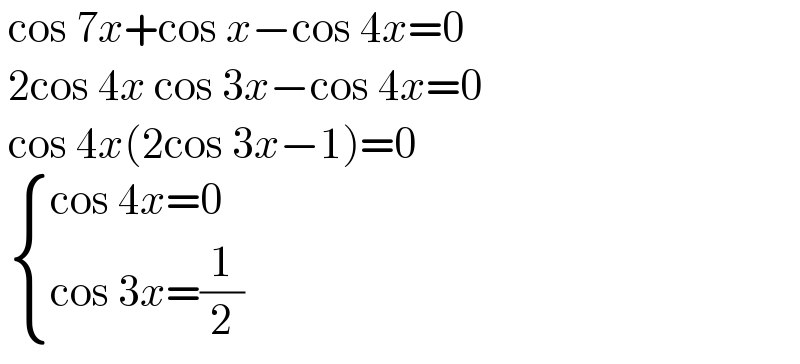
$$\:\mathrm{cos}\:\mathrm{7}{x}+\mathrm{cos}\:{x}−\mathrm{cos}\:\mathrm{4}{x}=\mathrm{0} \\ $$$$\:\mathrm{2cos}\:\mathrm{4}{x}\:\mathrm{cos}\:\mathrm{3}{x}−\mathrm{cos}\:\mathrm{4}{x}=\mathrm{0} \\ $$$$\:\mathrm{cos}\:\mathrm{4}{x}\left(\mathrm{2cos}\:\mathrm{3}{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\begin{cases}{\mathrm{cos}\:\mathrm{4}{x}=\mathrm{0}}\\{\mathrm{cos}\:\mathrm{3}{x}=\frac{\mathrm{1}}{\mathrm{2}}}\end{cases} \\ $$
Answered by gsk2684 last updated on 22/Oct/21
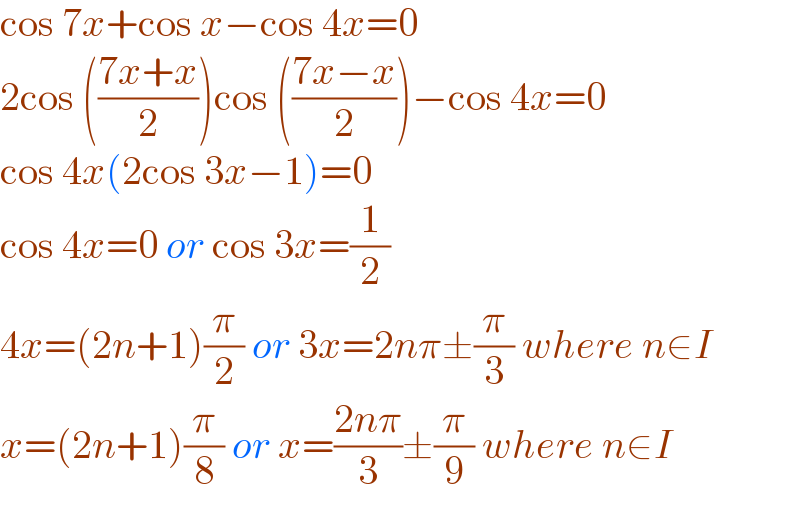
$$\mathrm{cos}\:\mathrm{7}{x}+\mathrm{cos}\:{x}−\mathrm{cos}\:\mathrm{4}{x}=\mathrm{0} \\ $$$$\mathrm{2cos}\:\left(\frac{\mathrm{7}{x}+{x}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\mathrm{7}{x}−{x}}{\mathrm{2}}\right)−\mathrm{cos}\:\mathrm{4}{x}=\mathrm{0} \\ $$$$\mathrm{cos}\:\mathrm{4}{x}\left(\mathrm{2cos}\:\mathrm{3}{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{cos}\:\mathrm{4}{x}=\mathrm{0}\:{or}\:\mathrm{cos}\:\mathrm{3}{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{4}{x}=\left(\mathrm{2}{n}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}}\:{or}\:\mathrm{3}{x}=\mathrm{2}{n}\pi\pm\frac{\pi}{\mathrm{3}}\:{where}\:{n}\in{I} \\ $$$${x}=\left(\mathrm{2}{n}+\mathrm{1}\right)\frac{\pi}{\mathrm{8}}\:{or}\:{x}=\frac{\mathrm{2}{n}\pi}{\mathrm{3}}\pm\frac{\pi}{\mathrm{9}}\:{where}\:{n}\in{I} \\ $$
