Question Number 26368 by d.monhbayr@gmail.com last updated on 24/Dec/17
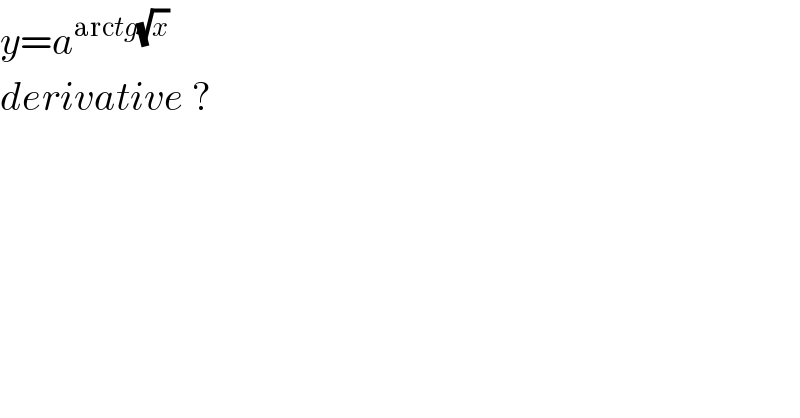
$${y}={a}^{\mathrm{arc}{tg}\sqrt{{x}}} \\ $$$${derivative}\:? \\ $$
Commented by kaivan.ahmadi last updated on 24/Dec/17
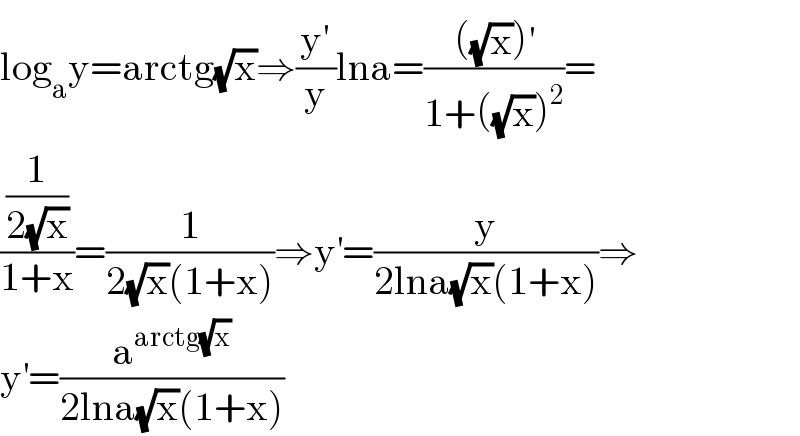
$$\mathrm{log}_{\mathrm{a}} \mathrm{y}=\mathrm{arctg}\sqrt{\mathrm{x}}\Rightarrow\frac{\mathrm{y}'}{\mathrm{y}}\mathrm{lna}=\frac{\left(\sqrt{\mathrm{x}}\right)^{'} }{\mathrm{1}+\left(\sqrt{\mathrm{x}}\right)^{\mathrm{2}} }= \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}}{\mathrm{1}+\mathrm{x}}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}\left(\mathrm{1}+\mathrm{x}\right)}\Rightarrow\mathrm{y}^{'} =\frac{\mathrm{y}}{\mathrm{2lna}\sqrt{\mathrm{x}}\left(\mathrm{1}+\mathrm{x}\right)}\Rightarrow \\ $$$$\mathrm{y}^{'} =\frac{\mathrm{a}^{\mathrm{arctg}\sqrt{\mathrm{x}}} }{\mathrm{2lna}\sqrt{\mathrm{x}}\left(\mathrm{1}+\mathrm{x}\right)} \\ $$
