Question Number 26449 by Tinkutara last updated on 25/Dec/17
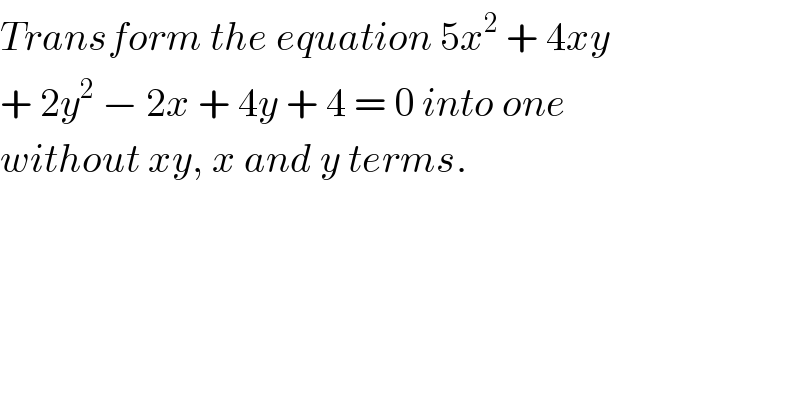
$${Transform}\:{the}\:{equation}\:\mathrm{5}{x}^{\mathrm{2}} \:+\:\mathrm{4}{xy} \\ $$$$+\:\mathrm{2}{y}^{\mathrm{2}} \:−\:\mathrm{2}{x}\:+\:\mathrm{4}{y}\:+\:\mathrm{4}\:=\:\mathrm{0}\:{into}\:{one} \\ $$$${without}\:{xy},\:{x}\:{and}\:{y}\:{terms}. \\ $$
Answered by jota@ last updated on 26/Dec/17
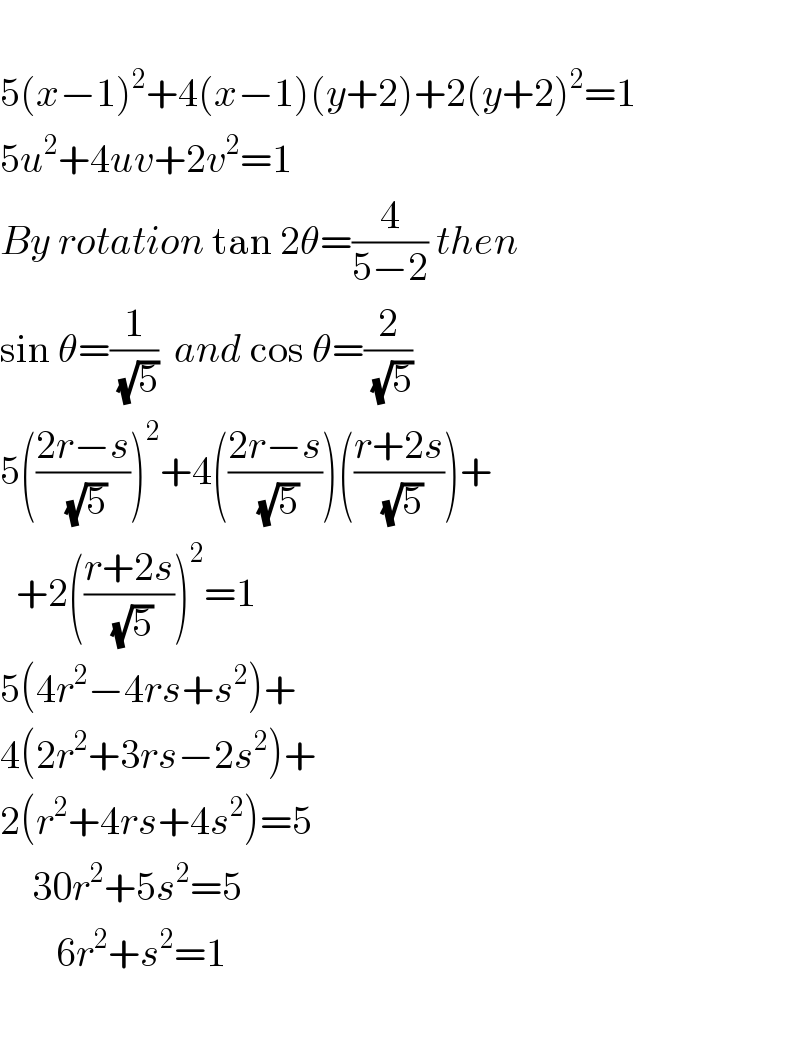
$$ \\ $$$$\mathrm{5}\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}\left({x}−\mathrm{1}\right)\left({y}+\mathrm{2}\right)+\mathrm{2}\left({y}+\mathrm{2}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{5}{u}^{\mathrm{2}} +\mathrm{4}{uv}+\mathrm{2}{v}^{\mathrm{2}} =\mathrm{1} \\ $$$${By}\:{rotation}\:\mathrm{tan}\:\mathrm{2}\theta=\frac{\mathrm{4}}{\mathrm{5}−\mathrm{2}}\:{then} \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\:\:{and}\:\mathrm{cos}\:\theta=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}} \\ $$$$\mathrm{5}\left(\frac{\mathrm{2}{r}−{s}}{\:\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} +\mathrm{4}\left(\frac{\mathrm{2}{r}−{s}}{\:\sqrt{\mathrm{5}}}\right)\left(\frac{{r}+\mathrm{2}{s}}{\:\sqrt{\mathrm{5}}}\right)+ \\ $$$$\:\:+\mathrm{2}\left(\frac{{r}+\mathrm{2}{s}}{\:\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{5}\left(\mathrm{4}{r}^{\mathrm{2}} −\mathrm{4}{rs}+{s}^{\mathrm{2}} \right)+ \\ $$$$\mathrm{4}\left(\mathrm{2}{r}^{\mathrm{2}} +\mathrm{3}{rs}−\mathrm{2}{s}^{\mathrm{2}} \right)+ \\ $$$$\mathrm{2}\left({r}^{\mathrm{2}} +\mathrm{4}{rs}+\mathrm{4}{s}^{\mathrm{2}} \right)=\mathrm{5} \\ $$$$\:\:\:\:\mathrm{30}{r}^{\mathrm{2}} +\mathrm{5}{s}^{\mathrm{2}} =\mathrm{5}\: \\ $$$$\:\:\:\:\:\:\:\mathrm{6}{r}^{\mathrm{2}} +{s}^{\mathrm{2}} =\mathrm{1} \\ $$$$\:\:\:\:\:\:\: \\ $$
Commented by Tinkutara last updated on 27/Dec/17
Thanks for this but how rotation formula is applied? Isn't it for angle bisectors between pairs of lines passing through origin?
Commented by ajfour last updated on 27/Dec/17
angular bisectors of a pair of
straight lines is the locus of
points having same distance
from the two lines. Rotation
wont be helpful.
Commented by Tinkutara last updated on 27/Dec/17
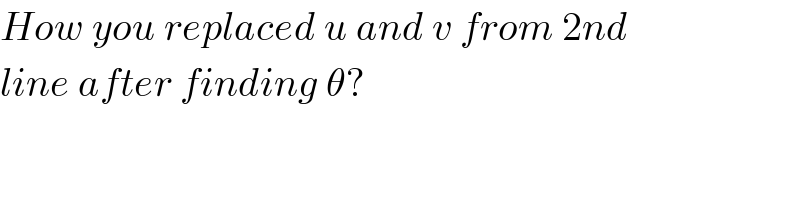
$${How}\:{you}\:{replaced}\:{u}\:{and}\:{v}\:{from}\:\mathrm{2}{nd} \\ $$$${line}\:{after}\:{finding}\:\theta? \\ $$
Commented by ajfour last updated on 27/Dec/17
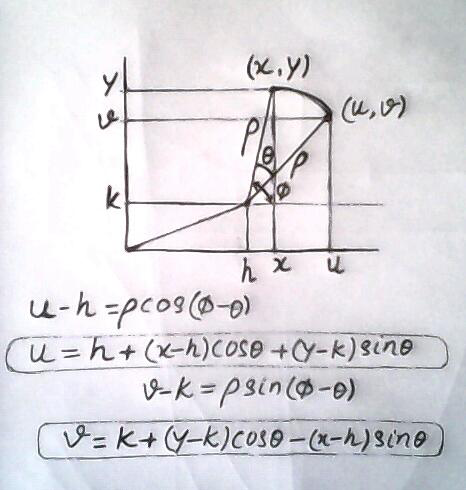
Commented by Tinkutara last updated on 27/Dec/17
I got it. Rotation will eliminate xy terms.
Commented by jota@ last updated on 28/Dec/17
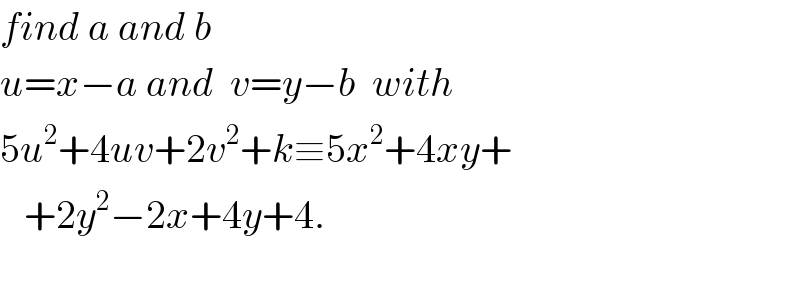
$${find}\:{a}\:{and}\:{b} \\ $$$${u}={x}−{a}\:{and}\:\:{v}={y}−{b}\:\:{with} \\ $$$$\mathrm{5}{u}^{\mathrm{2}} +\mathrm{4}{uv}+\mathrm{2}{v}^{\mathrm{2}} +{k}\equiv\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}{xy}+ \\ $$$$\:\:\:+\mathrm{2}{y}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}{y}+\mathrm{4}. \\ $$$$ \\ $$
