Menu Close

calculate-cos-arctan-2x-1-x-2-x-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 92078 by mathmax by abdo last updated on 04/May/20
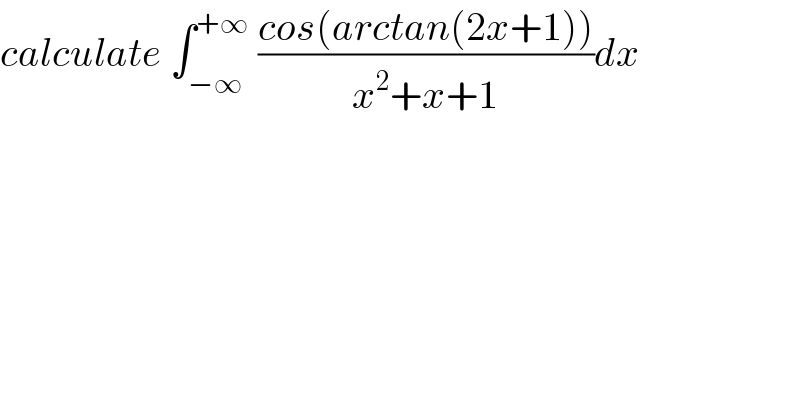
calculate ∫_(−∞) ^(+∞) ((cos(arctan(2x+1)))/(x^2 +x+1))dx
$${calculate}\:\int_{−\infty} ^{+\infty} \:\frac{{cos}\left({arctan}\left(\mathrm{2}{x}+\mathrm{1}\right)\right)}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx} \\ $$
Commented by abdomathmax last updated on 09/May/20
I =∫_(−∞) ^(+∞) ((cos(arctan(2x+1))dx)/(x^2 +x+1)) I =Re(∫_(−∞) ^(+∞) (e^(iarctan(2x+1)) /(x^2 +x+1))dx) let ϕ(z) =(e^(iarctan(2z+1)) /(z^2 +z+1)) poles of ϕ? z^2 +z+1 =0 →Δ=−3 ⇒ z_1 =((−1+i(√3))/2) =e^(i((2π)/3)) and z_2 =((−1−i(√3))/2) =e^(−((i2π)/3)) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,e^((i2π)/3) ) Res(ϕ,e^((i2π)/3) ) =(e^(iarctan(2 z_1 +1)) /((z_1 −z_2 ))) =(e^(iarctan(2e^((i2π)/3) +1)) /(2i×((√3)/2))) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =((2π)/( (√3))) e^(i arctan(2e^((i2π)/3) +1)) we know arctan(z) =(1/(2i))ln(((1+iz)/(1−iz))) 2e^((i2π)/3) +1 =2(−(1/2)+i((√3)/2))+1 =i(√3) ⇒ arctan(...) =arctan(i(√3)) =(1/(2i))ln(((1+i(i(√3)))/(1−i(i(√3))))) =(1/(2i))ln(((1−(√3))/(1+(√3)))) =(1/(2i))ln(−1) +(1/(2i))ln((((√3)−1)/( (√3)+1))) =((iπ)/(2i)) +(1/(2i))ln((((√3)−1)/( (√3)+1))) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =((2π)/( (√3)))((π/2)+(1/(2i))ln((((√3)−1)/( (√3)+1)))) =(π^2 /( (√3))) +−((iπ)/( (√3)))ln((((√3)−1)/( (√3)+1))) I =Re(∫_(−∞) ^(+∞) ϕ(z)dz ) =(π^2 /( (√3)))
$${I}\:=\int_{−\infty} ^{+\infty} \:\frac{{cos}\left({arctan}\left(\mathrm{2}{x}+\mathrm{1}\right)\right){dx}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}\: \\ $$$${I}\:={Re}\left(\int_{−\infty} ^{+\infty} \:\frac{{e}^{{iarctan}\left(\mathrm{2}{x}+\mathrm{1}\right)} }{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}{dx}\right)\:{let}\:\varphi\left({z}\right)\:=\frac{{e}^{{iarctan}\left(\mathrm{2}{z}+\mathrm{1}\right)} }{{z}^{\mathrm{2}} \:+{z}+\mathrm{1}} \\ $$$${poles}\:{of}\:\varphi?\:\:\:{z}^{\mathrm{2}} \:+{z}+\mathrm{1}\:=\mathrm{0}\:\rightarrow\Delta=−\mathrm{3}\:\Rightarrow \\ $$$${z}_{\mathrm{1}} =\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:={e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \:\:\:{and}\:{z}_{\mathrm{2}} =\frac{−\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:={e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \\ $$$${residus}\:{theorem}\:{give}\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right) \\ $$$${Res}\left(\varphi,{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)\:=\frac{{e}^{{iarctan}\left(\mathrm{2}\:{z}_{\mathrm{1}} +\mathrm{1}\right)} }{\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)}\:=\frac{{e}^{{iarctan}\left(\mathrm{2}{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} +\mathrm{1}\right)} }{\mathrm{2}{i}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}}\:{e}^{{i}\:{arctan}\left(\mathrm{2}{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \:+\mathrm{1}\right)} \\ $$$${we}\:{know}\:\:{arctan}\left({z}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}+{iz}}{\mathrm{1}−{iz}}\right) \\ $$$$\mathrm{2}{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \:+\mathrm{1}\:=\mathrm{2}\left(−\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)+\mathrm{1}\:={i}\sqrt{\mathrm{3}}\:\Rightarrow \\ $$$${arctan}\left(…\right)\:={arctan}\left({i}\sqrt{\mathrm{3}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}+{i}\left({i}\sqrt{\mathrm{3}}\right)}{\mathrm{1}−{i}\left({i}\sqrt{\mathrm{3}}\right)}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{1}+\sqrt{\mathrm{3}}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(−\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\:\sqrt{\mathrm{3}}+\mathrm{1}}\right) \\ $$$$=\frac{{i}\pi}{\mathrm{2}{i}}\:+\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\:\sqrt{\mathrm{3}}+\mathrm{1}}\right)\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}}\left(\frac{\pi}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\:\sqrt{\mathrm{3}}+\mathrm{1}}\right)\right) \\ $$$$=\frac{\pi^{\mathrm{2}} }{\:\sqrt{\mathrm{3}}}\:+−\frac{{i}\pi}{\:\sqrt{\mathrm{3}}}{ln}\left(\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\:\sqrt{\mathrm{3}}+\mathrm{1}}\right)\: \\ $$$${I}\:={Re}\left(\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:\right)\:=\frac{\pi^{\mathrm{2}} }{\:\sqrt{\mathrm{3}}} \\ $$
Commented by Ar Brandon last updated on 09/May/20
nice

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *