Menu Close

find-the-value-of-0-1-x-E-1-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 26569 by abdo imad last updated on 26/Dec/17
find the value of ∫_0 ^(1 ) x E((1/x))dx
$${find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\mathrm{1}\:} {x}\:{E}\left(\frac{\mathrm{1}}{{x}}\right){dx}\: \\ $$
Commented by abdo imad last updated on 30/Dec/17
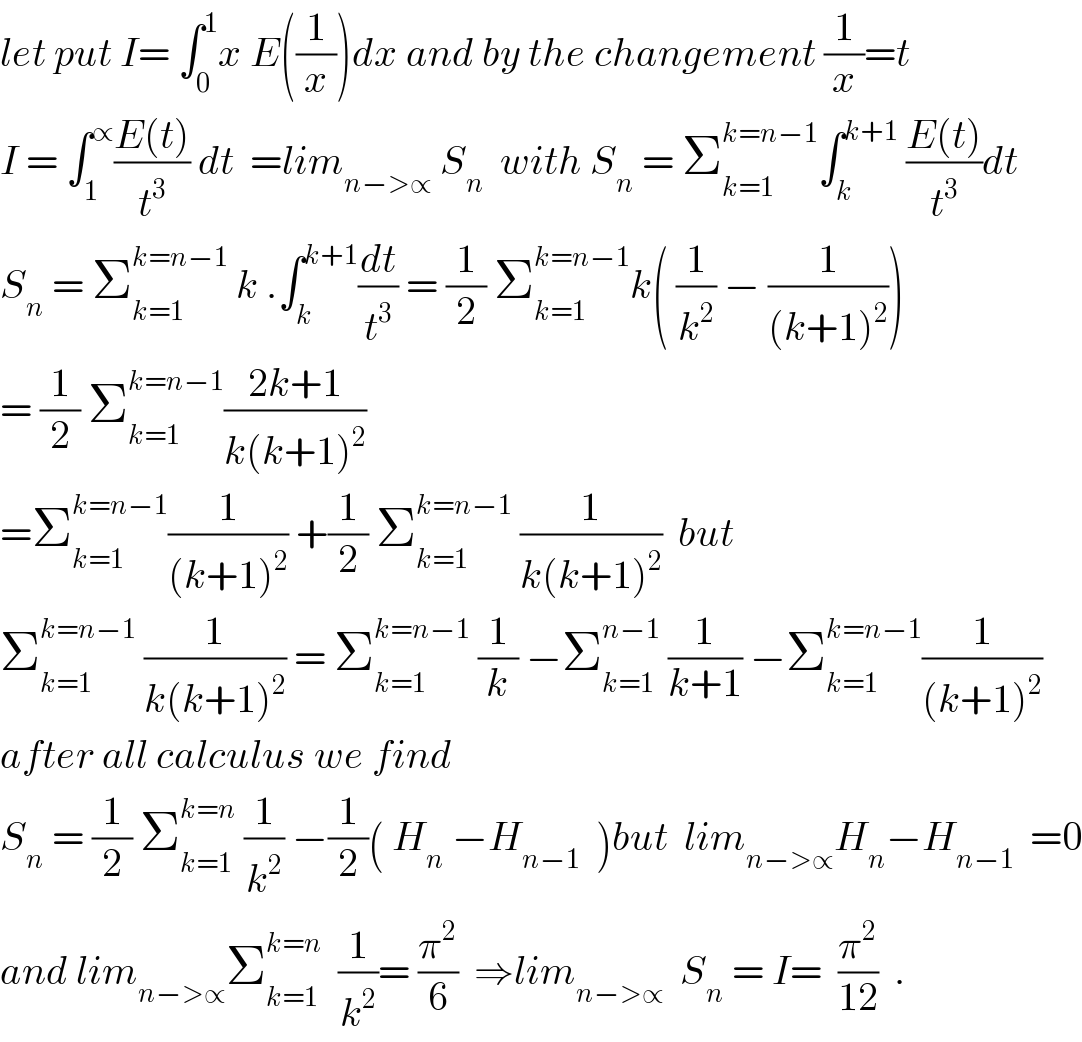
let put I= ∫_0 ^1 x E((1/x))dx and by the changement (1/x)=t I = ∫_1 ^∝ ((E(t))/t^3 ) dt =lim_(n−>∝) S_n with S_n = Σ_(k=1) ^(k=n−1) ∫_k ^(k+1) ((E(t))/t^3 )dt S_n = Σ_(k=1) ^(k=n−1) k .∫_k ^(k+1) (dt/t^3 ) = (1/2) Σ_(k=1) ^(k=n−1) k( (1/k^2 ) − (1/((k+1)^2 ))) = (1/2) Σ_(k=1) ^(k=n−1) ((2k+1)/(k(k+1)^2 )) =Σ_(k=1) ^(k=n−1) (1/((k+1)^2 )) +(1/2) Σ_(k=1) ^(k=n−1) (1/(k(k+1)^2 )) but Σ_(k=1) ^(k=n−1) (1/(k(k+1)^2 )) = Σ_(k=1) ^(k=n−1) (1/k) −Σ_(k=1) ^(n−1) (1/(k+1)) −Σ_(k=1) ^(k=n−1) (1/((k+1)^2 )) after all calculus we find S_n = (1/2) Σ_(k=1) ^(k=n) (1/k^2 ) −(1/2)( H_n −H_(n−1) )but lim_(n−>∝) H_n −H_(n−1) =0 and lim_(n−>∝) Σ_(k=1) ^(k=n) (1/k^2 )= (π^2 /6) ⇒lim_(n−>∝) S_n = I= (π^2 /(12)) .
$${let}\:{put}\:{I}=\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}\:{E}\left(\frac{\mathrm{1}}{{x}}\right){dx}\:{and}\:{by}\:{the}\:{changement}\:\frac{\mathrm{1}}{{x}}={t} \\ $$$${I}\:=\:\int_{\mathrm{1}} ^{\propto} \frac{{E}\left({t}\right)}{{t}^{\mathrm{3}} }\:{dt}\:\:={lim}_{{n}−>\propto} \:{S}_{{n}} \:\:{with}\:{S}_{{n}} \:=\:\sum_{{k}=\mathrm{1}} ^{{k}={n}−\mathrm{1}} \int_{{k}} ^{{k}+\mathrm{1}} \:\frac{{E}\left({t}\right)}{{t}^{\mathrm{3}} }{dt} \\ $$$${S}_{{n}} \:=\:\sum_{{k}=\mathrm{1}} ^{{k}={n}−\mathrm{1}} \:{k}\:.\int_{{k}} ^{{k}+\mathrm{1}} \frac{{dt}}{{t}^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{k}=\mathrm{1}} ^{{k}={n}−\mathrm{1}} {k}\left(\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{k}=\mathrm{1}} ^{{k}={n}−\mathrm{1}} \frac{\mathrm{2}{k}+\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\sum_{{k}=\mathrm{1}} ^{{k}={n}−\mathrm{1}} \frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{k}=\mathrm{1}} ^{{k}={n}−\mathrm{1}} \:\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)^{\mathrm{2}} }\:\:{but} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{k}={n}−\mathrm{1}} \:\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)^{\mathrm{2}} }\:=\:\sum_{{k}=\mathrm{1}} ^{{k}={n}−\mathrm{1}} \:\frac{\mathrm{1}}{{k}}\:−\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\frac{\mathrm{1}}{{k}+\mathrm{1}}\:−\sum_{{k}=\mathrm{1}} ^{{k}={n}−\mathrm{1}} \frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${after}\:{all}\:{calculus}\:{we}\:{find}\: \\ $$$${S}_{{n}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\:{H}_{{n}} \:−{H}_{{n}−\mathrm{1}} \:\:\right){but}\:\:{lim}_{{n}−>\propto} {H}_{{n}} −{H}_{{n}−\mathrm{1}} \:\:=\mathrm{0} \\ $$$${and}\:{lim}_{{n}−>\propto} \sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:\:\Rightarrow{lim}_{{n}−>\propto} \:\:{S}_{{n}} \:=\:{I}=\:\:\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *