Question Number 26889 by shiva123 last updated on 31/Dec/17
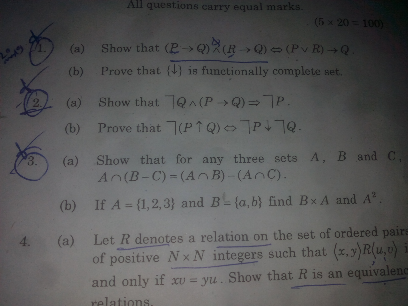
Answered by prakash jain last updated on 31/Dec/17
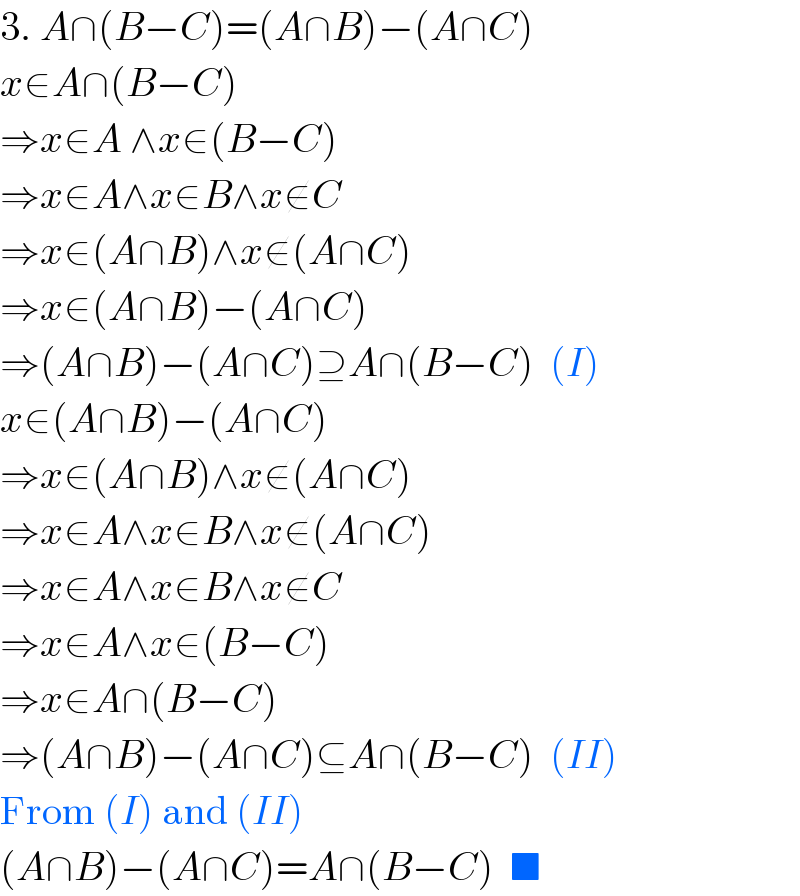
$$\mathrm{3}.\:{A}\cap\left({B}−{C}\right)=\left({A}\cap{B}\right)−\left({A}\cap{C}\right) \\ $$$${x}\in{A}\cap\left({B}−{C}\right) \\ $$$$\Rightarrow{x}\in{A}\:\wedge{x}\in\left({B}−{C}\right) \\ $$$$\Rightarrow{x}\in{A}\wedge{x}\in{B}\wedge{x}\notin{C} \\ $$$$\Rightarrow{x}\in\left({A}\cap{B}\right)\wedge{x}\notin\left({A}\cap{C}\right) \\ $$$$\Rightarrow{x}\in\left({A}\cap{B}\right)−\left({A}\cap{C}\right) \\ $$$$\Rightarrow\left({A}\cap{B}\right)−\left({A}\cap{C}\right)\supseteq{A}\cap\left({B}−{C}\right)\:\:\left({I}\right) \\ $$$${x}\in\left({A}\cap{B}\right)−\left({A}\cap{C}\right) \\ $$$$\Rightarrow{x}\in\left({A}\cap{B}\right)\wedge{x}\notin\left({A}\cap{C}\right) \\ $$$$\Rightarrow{x}\in{A}\wedge{x}\in{B}\wedge{x}\notin\left({A}\cap{C}\right) \\ $$$$\Rightarrow{x}\in{A}\wedge{x}\in{B}\wedge{x}\notin{C} \\ $$$$\Rightarrow{x}\in{A}\wedge{x}\in\left({B}−{C}\right) \\ $$$$\Rightarrow{x}\in{A}\cap\left({B}−{C}\right)\:\: \\ $$$$\Rightarrow\left({A}\cap{B}\right)−\left({A}\cap{C}\right)\subseteq{A}\cap\left({B}−{C}\right)\:\:\left({II}\right) \\ $$$$\mathrm{From}\:\left({I}\right)\:\mathrm{and}\:\left({II}\right) \\ $$$$\left({A}\cap{B}\right)−\left({A}\cap{C}\right)={A}\cap\left({B}−{C}\right)\:\:\blacksquare \\ $$
