Question Number 27000 by abdo imad last updated on 01/Jan/18
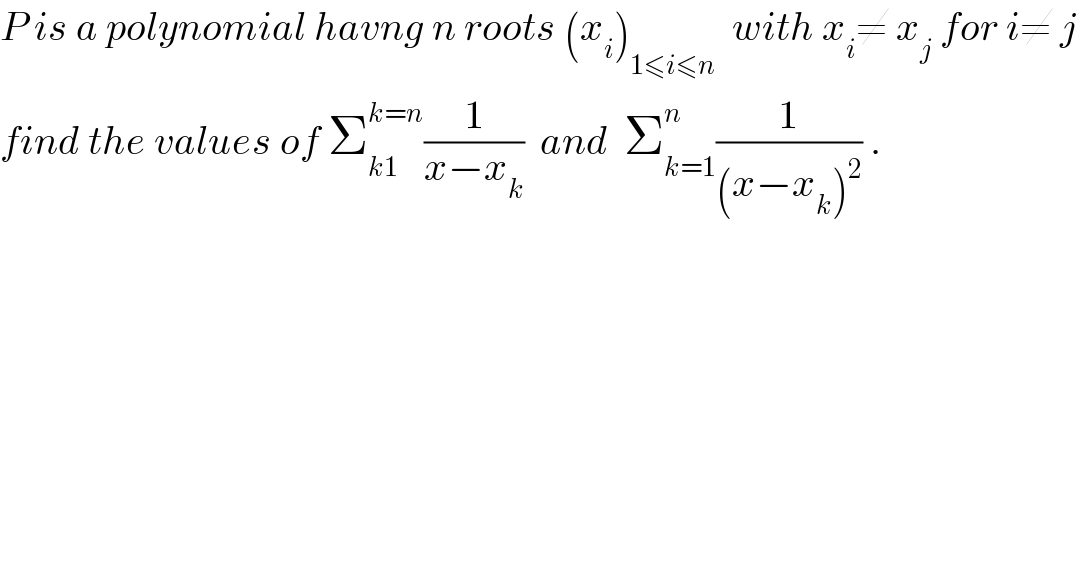
$${P}\:{is}\:{a}\:{polynomial}\:{havng}\:{n}\:{roots}\:\left({x}_{{i}} \right)_{\mathrm{1}\leqslant{i}\leqslant{n}} \:\:{with}\:{x}_{{i}} \neq\:{x}_{{j}} \:{for}\:{i}\neq\:{j} \\ $$$${find}\:{the}\:{values}\:{of}\:\sum_{{k}\mathrm{1}} ^{{k}={n}} \frac{\mathrm{1}}{{x}−{x}_{{k}} }\:\:{and}\:\:\sum_{{k}=\mathrm{1}} ^{{n}} \frac{\mathrm{1}}{\left({x}−{x}_{{k}} \right)^{\mathrm{2}} }\:. \\ $$
Commented by abdo imad last updated on 01/Jan/18
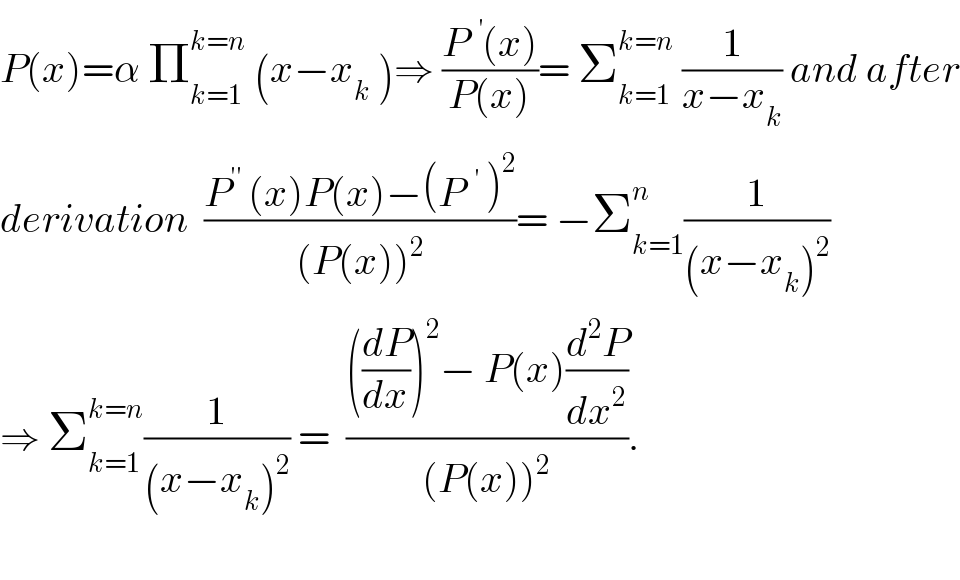
$${P}\left({x}\right)=\alpha\:\prod_{{k}=\mathrm{1}} ^{{k}={n}} \:\left({x}−{x}_{{k}} \:\right)\Rightarrow\:\frac{{P}^{} \left({x}\right)}{{P}\left({x}\right)}=\:\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\frac{\mathrm{1}}{{x}−{x}_{{k}} }\:{and}\:{after} \\ $$$${derivation}\:\:\frac{{P}^{'^{'} } \:\left({x}\right){P}\left({x}\right)−\left({P}^{} \:\right)^{\mathrm{2}} }{\left({P}\left({x}\right)\right)^{\mathrm{2}} }=\:−\sum_{{k}=\mathrm{1}} ^{{n}} \frac{\mathrm{1}}{\left({x}−{x}_{{k}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:\sum_{{k}=\mathrm{1}} ^{{k}={n}} \frac{\mathrm{1}}{\left({x}−{x}_{{k}} \right)^{\mathrm{2}} }\:=\:\:\frac{\left(\frac{{dP}}{{dx}}\right)^{\mathrm{2}} −\:{P}\left({x}\right)\frac{{d}^{\mathrm{2}} {P}}{{dx}^{\mathrm{2}} }}{\left({P}\left({x}\right)\right)^{\mathrm{2}} }. \\ $$$$ \\ $$
