Question Number 92668 by john santu last updated on 08/May/20
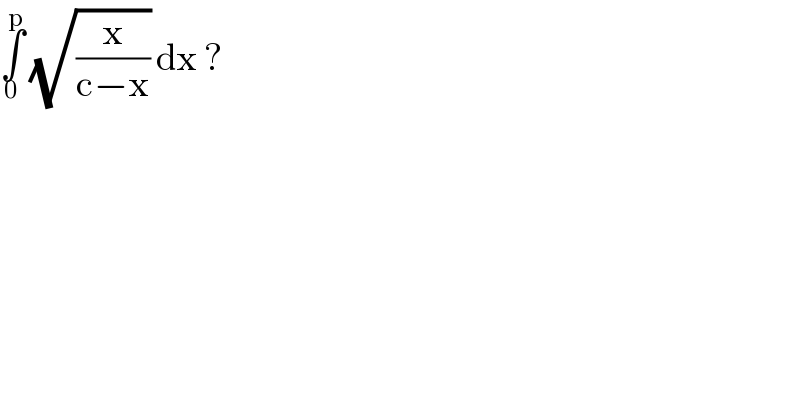
$$\underset{\mathrm{0}} {\overset{\mathrm{p}} {\int}}\:\sqrt{\frac{\mathrm{x}}{\mathrm{c}−\mathrm{x}}}\:\mathrm{dx}\:?\: \\ $$
Commented by john santu last updated on 08/May/20
![set t = (√(x/(c−x))) , x = ((ct^2 )/(1+t^2 )) dx = ((2ct dt)/((1+t^2 )^2 )) I = ∫_0 ^(√(p/(c−p))) (( 2ct^2 dt)/((1+t^2 )^2 )) I= −c [(t/(1+t^2 ))]_0 ^(√(p/(c−p))) + c[tan^(−1) t]_0 ^(√(p/(c−p))) =−c [((√(p/(c−p)))/(1+(p/(c−p)))) ] +c [tan^(−1) (√(p/(c−p)))]](https://www.tinkutara.com/question/Q92688.png)
$$\mathrm{set}\:\mathrm{t}\:=\:\sqrt{\frac{{x}}{{c}−{x}}}\:,\:{x}\:=\:\frac{{ct}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:\: \\ $$$${dx}\:=\:\frac{\mathrm{2}{ct}\:{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\: \\ $$$${I}\:=\:\underset{\mathrm{0}} {\overset{\sqrt{\frac{\mathrm{p}}{\mathrm{c}−\mathrm{p}}}} {\int}}\frac{\:\:\mathrm{2}{ct}^{\mathrm{2}} \:{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\: \\ $$$${I}=\:−\mathrm{c}\:\left[\frac{\mathrm{t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\sqrt{\frac{\mathrm{p}}{\mathrm{c}−\mathrm{p}}}} +\:\mathrm{c}\left[\mathrm{tan}^{−\mathrm{1}} \:\mathrm{t}\right]_{\mathrm{0}} ^{\sqrt{\frac{\mathrm{p}}{\mathrm{c}−\mathrm{p}}}} \\ $$$$=−\mathrm{c}\:\left[\frac{\sqrt{\frac{\mathrm{p}}{\mathrm{c}−\mathrm{p}}}}{\mathrm{1}+\frac{\mathrm{p}}{\mathrm{c}−\mathrm{p}}}\:\right]\:+\mathrm{c}\:\left[\mathrm{tan}^{−\mathrm{1}} \:\sqrt{\frac{\mathrm{p}}{\mathrm{c}−\mathrm{p}}}\right]\: \\ $$
Commented by mathmax by abdo last updated on 08/May/20
![I =∫_0 ^p (√(x/(c−x)))dx changement x=csin^2 t give I =∫_0 ^(arcsin((√(p/c)))) (√((csin^2 t)/(ccos^2 t)))2csint cost =2c∫_0 ^(arcsin((√(p/c)))) ((sint)/(cost)) sint cost dt =2c ∫_0 ^(arcsin((√(p/c)))) ((1−cos(2t))/2)dt =c arcsin((√(p/c)))−(c/2) [sin(2t)]_0 ^(arcsin((√(p/c)))) +λ =c arcsin((√(p/c)))−c[sint (√(1−sin^2 t))]_0 ^(arcsin((√(p/c)))) +λ =c arcsin((√(p/c)))−c(√(p/c))(√(1−(p/c))) +λ =c arcsin((√(p/c)))−(√(p(c−p))) +λ](https://www.tinkutara.com/question/Q92713.png)
$${I}\:=\int_{\mathrm{0}} ^{{p}} \sqrt{\frac{{x}}{{c}−{x}}}{dx}\:\:{changement}\:{x}={csin}^{\mathrm{2}} {t}\:{give} \\ $$$${I}\:=\int_{\mathrm{0}} ^{{arcsin}\left(\sqrt{\frac{{p}}{{c}}}\right)} \sqrt{\frac{{csin}^{\mathrm{2}} {t}}{{ccos}^{\mathrm{2}} {t}}}\mathrm{2}{csint}\:{cost} \\ $$$$=\mathrm{2}{c}\int_{\mathrm{0}} ^{{arcsin}\left(\sqrt{\frac{{p}}{{c}}}\right)} \:\frac{{sint}}{{cost}}\:{sint}\:{cost}\:{dt}\:=\mathrm{2}{c}\:\int_{\mathrm{0}} ^{{arcsin}\left(\sqrt{\frac{{p}}{{c}}}\right)} \:\frac{\mathrm{1}−{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}{dt} \\ $$$$={c}\:{arcsin}\left(\sqrt{\frac{{p}}{{c}}}\right)−\frac{{c}}{\mathrm{2}}\:\left[{sin}\left(\mathrm{2}{t}\right)\right]_{\mathrm{0}} ^{{arcsin}\left(\sqrt{\frac{{p}}{{c}}}\right)} \:+\lambda \\ $$$$={c}\:{arcsin}\left(\sqrt{\frac{{p}}{{c}}}\right)−{c}\left[{sint}\:\sqrt{\mathrm{1}−{sin}^{\mathrm{2}} {t}}\right]_{\mathrm{0}} ^{{arcsin}\left(\sqrt{\frac{{p}}{{c}}}\right)} \:+\lambda \\ $$$$={c}\:{arcsin}\left(\sqrt{\frac{{p}}{{c}}}\right)−{c}\sqrt{\frac{{p}}{{c}}}\sqrt{\mathrm{1}−\frac{{p}}{{c}}}\:+\lambda \\ $$$$={c}\:{arcsin}\left(\sqrt{\frac{{p}}{{c}}}\right)−\sqrt{{p}\left({c}−{p}\right)}\:+\lambda \\ $$
Answered by behi83417@gmail.com last updated on 08/May/20
![x=c.cos^2 t⇒dx=−2csint.costdt ⇒I=∫((cost)/(sint)).(−2c.sint.cost)dt= =−∫2ccos^2 tdt=−c∫(1+cos2t)dt= =−c(t+sint.cost)+const.= =−c.cos^(−1) (√((x/c) ))−(√(cx−x^2 ))+const. [I=∫_0 ^p (√(x/(c−x)))=((c.π)/2)−c.cos^(−1) (√(p/c))−(√(c.p−p^2 ))] [cost=(√(x/c)),sint=(√(1−(x/c))) ]](https://www.tinkutara.com/question/Q92677.png)
$$\mathrm{x}=\mathrm{c}.\mathrm{cos}^{\mathrm{2}} \mathrm{t}\Rightarrow\mathrm{dx}=−\mathrm{2csint}.\mathrm{costdt} \\ $$$$\Rightarrow\mathrm{I}=\int\frac{\mathrm{cost}}{\mathrm{sint}}.\left(−\mathrm{2c}.\mathrm{sint}.\mathrm{cost}\right)\mathrm{dt}= \\ $$$$=−\int\mathrm{2ccos}^{\mathrm{2}} \mathrm{tdt}=−\mathrm{c}\int\left(\mathrm{1}+\mathrm{cos2t}\right)\mathrm{dt}= \\ $$$$=−\mathrm{c}\left(\mathrm{t}+\mathrm{sint}.\mathrm{cost}\right)+\mathrm{const}.= \\ $$$$=−\mathrm{c}.\mathrm{cos}^{−\mathrm{1}} \sqrt{\frac{\mathrm{x}}{\mathrm{c}}\:}−\sqrt{\mathrm{cx}−\mathrm{x}^{\mathrm{2}} }+\mathrm{const}. \\ $$$$\left[\mathrm{I}=\underset{\mathrm{0}} {\overset{\mathrm{p}} {\int}}\sqrt{\frac{\mathrm{x}}{\mathrm{c}−\mathrm{x}}}=\frac{\boldsymbol{\mathrm{c}}.\pi}{\mathrm{2}}−\boldsymbol{\mathrm{c}}.\boldsymbol{\mathrm{cos}}^{−\mathrm{1}} \sqrt{\frac{\boldsymbol{\mathrm{p}}}{\boldsymbol{\mathrm{c}}}}−\sqrt{\boldsymbol{\mathrm{c}}.\boldsymbol{\mathrm{p}}−\boldsymbol{\mathrm{p}}^{\mathrm{2}} }\right] \\ $$$$\left[\mathrm{cost}=\sqrt{\frac{\mathrm{x}}{\mathrm{c}}},\mathrm{sint}=\sqrt{\mathrm{1}−\frac{\mathrm{x}}{\mathrm{c}}}\:\right] \\ $$
