Question Number 27180 by abdo imad last updated on 02/Jan/18
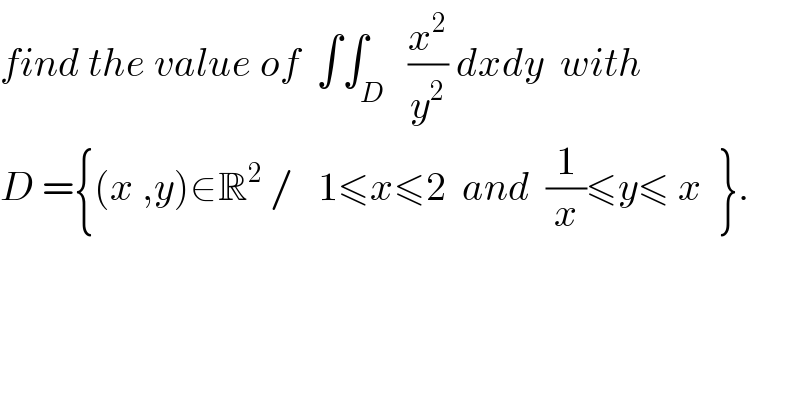
$${find}\:{the}\:{value}\:{of}\:\:\int\int_{{D}} \:\:\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }\:{dxdy}\:\:{with} \\ $$$${D}\:=\left\{\left({x}\:,{y}\right)\in\mathbb{R}^{\mathrm{2}} \:/\:\:\:\mathrm{1}\leqslant{x}\leqslant\mathrm{2}\:\:{and}\:\:\frac{\mathrm{1}}{{x}}\leqslant{y}\leqslant\:{x}\:\:\right\}. \\ $$
Commented by abdo imad last updated on 08/Jan/18
![∫∫_D (x^2 /y^2 )dxdy= ∫_1 ^2 (∫_(1/x) ^x (dy/y^2 ))x^2 dx = ∫_1 ^2 [−(1/y)]_(y=(1/x)) ^(y=x) x^2 dx=∫_1 ^2 x^2 (x−(1/x))dx = ∫_1 ^2 ( x^3 −x)dx= [(1/4)x^4 −(1/2) x^2 ]_1 ^2 = (1/4)[ x^4 −2x^2 ]_1 ^2 =(1/4)(( 16−8)−(−1))= (9/4) .](https://www.tinkutara.com/question/Q27550.png)
$$\int\int_{{D}} \frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }{dxdy}=\:\int_{\mathrm{1}} ^{\mathrm{2}} \left(\int_{\frac{\mathrm{1}}{{x}}} ^{{x}} \frac{{dy}}{{y}^{\mathrm{2}} }\right){x}^{\mathrm{2}} {dx} \\ $$$$=\:\int_{\mathrm{1}} ^{\mathrm{2}} \left[−\frac{\mathrm{1}}{{y}}\right]_{{y}=\frac{\mathrm{1}}{{x}}} ^{{y}={x}} {x}^{\mathrm{2}} {dx}=\int_{\mathrm{1}} ^{\mathrm{2}} \:{x}^{\mathrm{2}} \left({x}−\frac{\mathrm{1}}{{x}}\right){dx} \\ $$$$=\:\int_{\mathrm{1}} ^{\mathrm{2}} \left(\:{x}^{\mathrm{3}} −{x}\right){dx}=\:\left[\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{4}} \:−\frac{\mathrm{1}}{\mathrm{2}}\:{x}^{\mathrm{2}} \right]_{\mathrm{1}} ^{\mathrm{2}} =\:\frac{\mathrm{1}}{\mathrm{4}}\left[\:{x}^{\mathrm{4}} \:−\mathrm{2}{x}^{\mathrm{2}} \right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\left(\:\mathrm{16}−\mathrm{8}\right)−\left(−\mathrm{1}\right)\right)=\:\frac{\mathrm{9}}{\mathrm{4}}\:. \\ $$
