Menu Close

find-f-x-0-e-x-1-t-2-1-t-2-dt-interms-ofx-with-x-0-and-calculate-0-e-t-2-dt-

Tinku Tara 0 Comments
Pin




Question Number 27342 by abdo imad last updated on 05/Jan/18
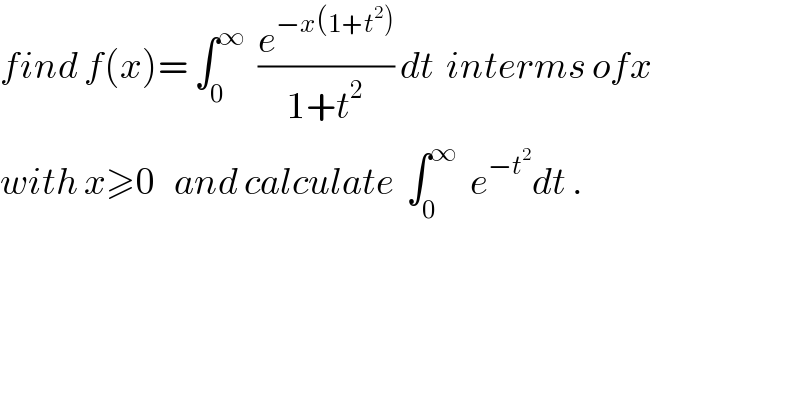
find f(x)= ∫_0 ^∞ (e^(−x(1+t^2 )) /(1+t^2 )) dt interms ofx with x≥0 and calculate ∫_0 ^∞ e^(−t^2 ) dt .
$${find}\:{f}\left({x}\right)=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{x}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} }{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt}\:\:{interms}\:{ofx} \\ $$$${with}\:{x}\geqslant\mathrm{0}\:\:\:{and}\:{calculate}\:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{t}^{\mathrm{2}} } {dt}\:. \\ $$
Commented by abdo imad last updated on 08/Jan/18
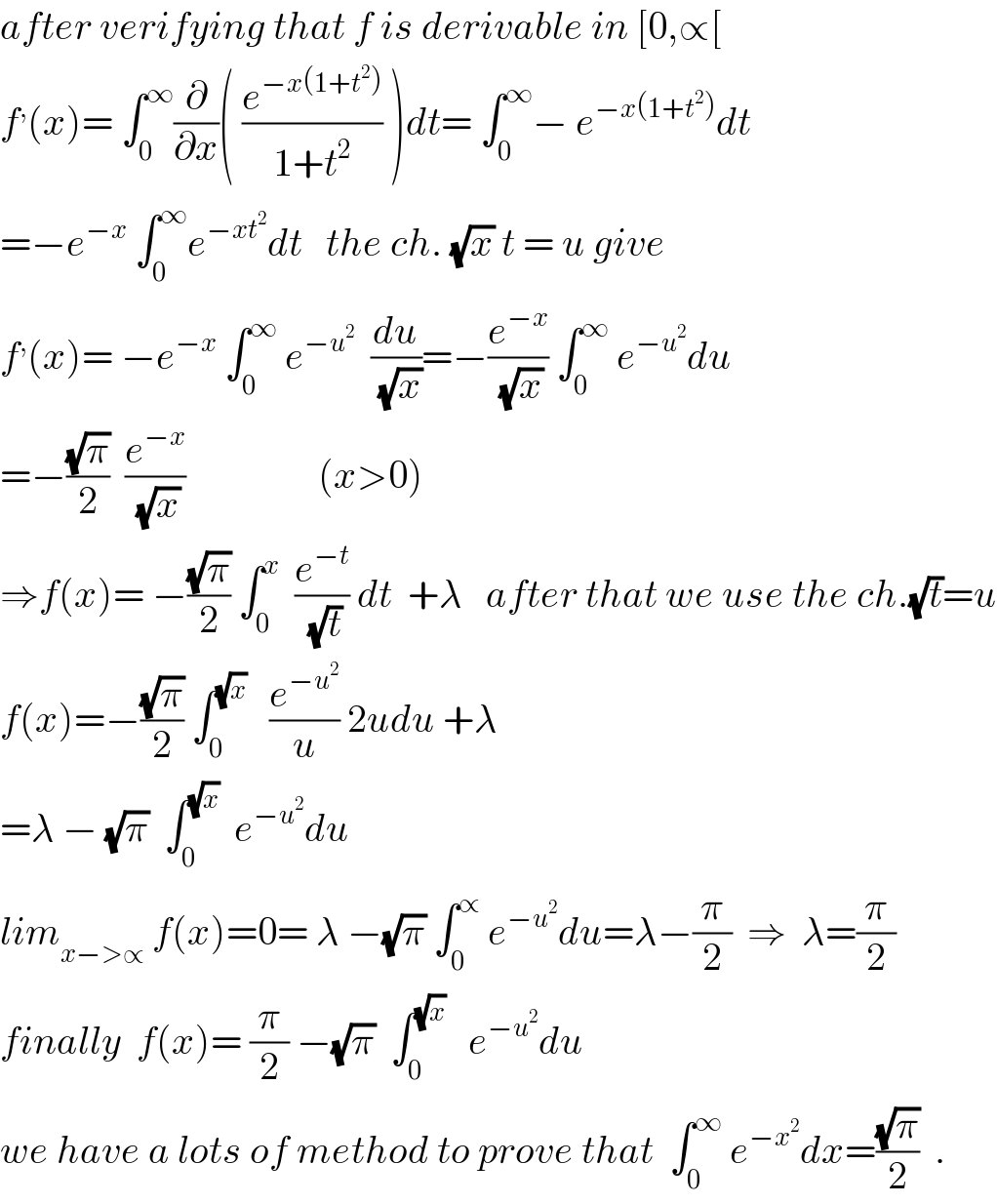
after verifying that f is derivable in [0,∝[ f^, (x)= ∫_0 ^∞ (∂/∂x)( (e^(−x(1+t^2 )) /(1+t^2 )) )dt= ∫_0 ^∞ − e^(−x(1+t^2 )) dt =−e^(−x) ∫_0 ^∞ e^(−xt^2 ) dt the ch. (√x) t = u give f^, (x)= −e^(−x) ∫_0 ^∞ e^(−u^2 ) (du/( (√x)))=−(e^(−x) /( (√x))) ∫_0 ^∞ e^(−u^2 ) du =−((√π)/2) (e^(−x) /( (√x))) (x>0) ⇒f(x)= −((√π)/2) ∫_0 ^x (e^(−t) /( (√t))) dt +λ after that we use the ch.(√t)=u f(x)=−((√π)/2) ∫_0 ^(√x) (e^(−u^2 ) /u) 2udu +λ =λ − (√π) ∫_0 ^(√x) e^(−u^2 ) du lim_(x−>∝) f(x)=0= λ −(√π) ∫_0 ^∝ e^(−u^2 ) du=λ−(π/2) ⇒ λ=(π/2) finally f(x)= (π/2) −(√π) ∫_0 ^(√x) e^(−u^2 ) du we have a lots of method to prove that ∫_0 ^∞ e^(−x^2 ) dx=((√π)/2) .
$${after}\:{verifying}\:{that}\:{f}\:{is}\:{derivable}\:{in}\:\left[\mathrm{0},\propto\left[\right.\right. \\ $$$${f}^{,} \left({x}\right)=\:\int_{\mathrm{0}} ^{\infty} \frac{\partial}{\partial{x}}\left(\:\frac{{e}^{−{x}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} }{\mathrm{1}+{t}^{\mathrm{2}} }\:\right){dt}=\:\int_{\mathrm{0}} ^{\infty} −\:{e}^{−{x}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} {dt} \\ $$$$=−{e}^{−{x}} \:\int_{\mathrm{0}} ^{\infty} {e}^{−{xt}^{\mathrm{2}} } {dt}\:\:\:{the}\:{ch}.\:\sqrt{{x}}\:{t}\:=\:{u}\:{give} \\ $$$${f}^{,} \left({x}\right)=\:−{e}^{−{x}} \:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{u}^{\mathrm{2}} } \:\:\frac{{du}}{\:\sqrt{{x}}}=−\frac{{e}^{−{x}} }{\:\sqrt{{x}}}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{u}^{\mathrm{2}} } {du} \\ $$$$=−\frac{\sqrt{\pi}}{\mathrm{2}}\:\:\frac{{e}^{−{x}} }{\:\sqrt{{x}}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({x}>\mathrm{0}\right) \\ $$$$\Rightarrow{f}\left({x}\right)=\:−\frac{\sqrt{\pi}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{x}} \:\:\frac{{e}^{−{t}} }{\:\sqrt{{t}}}\:{dt}\:\:+\lambda\:\:\:{after}\:{that}\:{we}\:{use}\:{the}\:{ch}.\sqrt{{t}}={u} \\ $$$${f}\left({x}\right)=−\frac{\sqrt{\pi}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\sqrt{{x}}} \:\:\:\frac{{e}^{−{u}^{\mathrm{2}} } }{{u}}\:\mathrm{2}{udu}\:+\lambda \\ $$$$=\lambda\:−\:\sqrt{\pi}\:\:\int_{\mathrm{0}} ^{\sqrt{{x}}} \:\:{e}^{−{u}^{\mathrm{2}} } {du} \\ $$$${lim}_{{x}−>\propto} \:{f}\left({x}\right)=\mathrm{0}=\:\lambda\:−\sqrt{\pi}\:\int_{\mathrm{0}} ^{\propto} \:{e}^{−{u}^{\mathrm{2}} } {du}=\lambda−\frac{\pi}{\mathrm{2}}\:\:\Rightarrow\:\:\lambda=\frac{\pi}{\mathrm{2}} \\ $$$${finally}\:\:{f}\left({x}\right)=\:\frac{\pi}{\mathrm{2}}\:−\sqrt{\pi}\:\:\int_{\mathrm{0}} ^{\sqrt{{x}}} \:\:\:{e}^{−{u}^{\mathrm{2}} } {du} \\ $$$${we}\:{have}\:{a}\:{lots}\:{of}\:{method}\:{to}\:{prove}\:{that}\:\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{x}^{\mathrm{2}} } {dx}=\frac{\sqrt{\pi}}{\mathrm{2}}\:\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *