Menu Close

Question-92885

Tinku Tara 0 Comments
Pin




Question Number 92885 by unknown last updated on 09/May/20
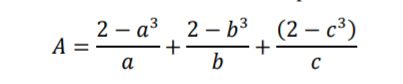
Commented by unknown last updated on 09/May/20
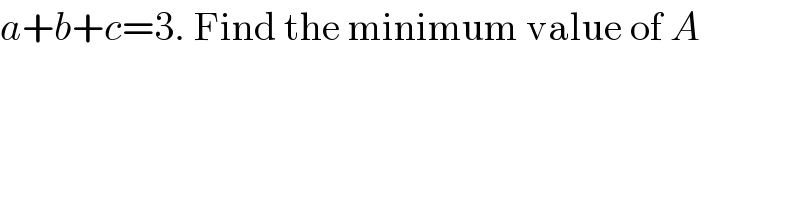
a+b+c=3. Find the minimum value of A
$${a}+{b}+{c}=\mathrm{3}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of}\:{A} \\ $$
Commented by mr W last updated on 09/May/20
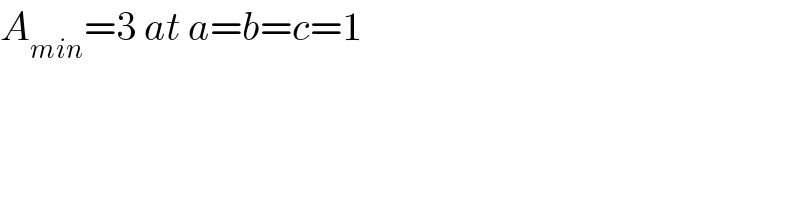
A_(min) =3 at a=b=c=1
$${A}_{{min}} =\mathrm{3}\:{at}\:{a}={b}={c}=\mathrm{1} \\ $$
Commented by prakash jain last updated on 10/May/20
If negative values allowed: a=102,b=1,c=−100? I also think question implictely assume +ve values.
$$\mathrm{If}\:\mathrm{negative}\:\mathrm{values}\:\mathrm{allowed}: \\ $$$${a}=\mathrm{102},{b}=\mathrm{1},{c}=−\mathrm{100}? \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{also}\:\mathrm{think}\:\mathrm{question}\:\mathrm{implictely} \\ $$$$\mathrm{assume}\:+\mathrm{ve}\:\mathrm{values}. \\ $$
Commented by unknown last updated on 10/May/20
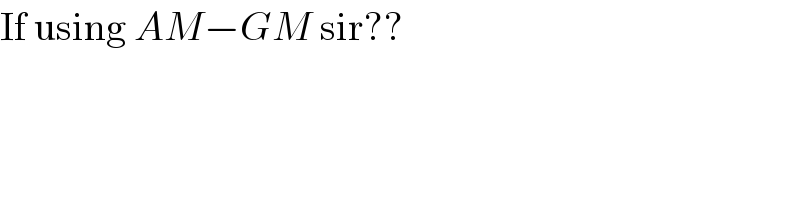
If using AM−GM sir??
$$\mathrm{If}\:\mathrm{using}\:{AM}−{GM}\:\mathrm{sir}?? \\ $$$$ \\ $$
Commented by mr W last updated on 10/May/20
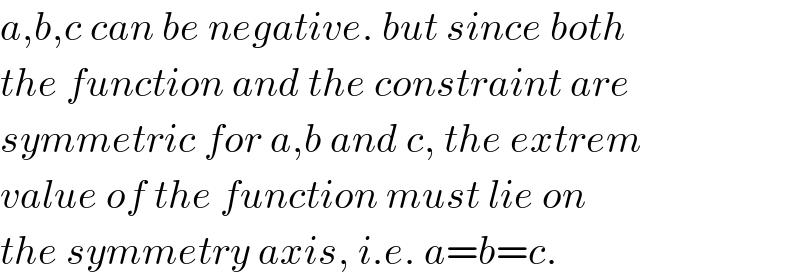
a,b,c can be negative. but since both the function and the constraint are symmetric for a,b and c, the extrem value of the function must lie on the symmetry axis, i.e. a=b=c.
$${a},{b},{c}\:{can}\:{be}\:{negative}.\:{but}\:{since}\:{both} \\ $$$${the}\:{function}\:{and}\:{the}\:{constraint}\:{are} \\ $$$${symmetric}\:{for}\:{a},{b}\:{and}\:{c},\:{the}\:{extrem} \\ $$$${value}\:{of}\:{the}\:{function}\:{must}\:{lie}\:{on} \\ $$$${the}\:{symmetry}\:{axis},\:{i}.{e}.\:{a}={b}={c}. \\ $$
Commented by prakash jain last updated on 10/May/20
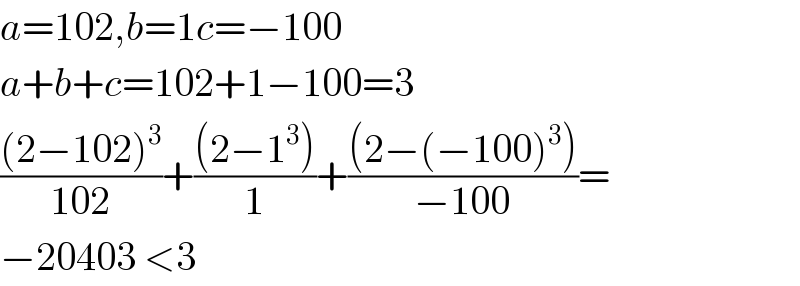
a=102,b=1c=−100 a+b+c=102+1−100=3 (((2−102)^3 )/(102))+(((2−1^3 ))/1)+(((2−(−100)^3 ))/(−100))= −20403 <3
$${a}=\mathrm{102},{b}=\mathrm{1}{c}=−\mathrm{100} \\ $$$${a}+{b}+{c}=\mathrm{102}+\mathrm{1}−\mathrm{100}=\mathrm{3} \\ $$$$\frac{\left(\mathrm{2}−\mathrm{102}\right)^{\mathrm{3}} }{\mathrm{102}}+\frac{\left(\mathrm{2}−\mathrm{1}^{\mathrm{3}} \right)}{\mathrm{1}}+\frac{\left(\mathrm{2}−\left(−\mathrm{100}\right)^{\mathrm{3}} \right)}{−\mathrm{100}}= \\ $$$$−\mathrm{20403}\:<\mathrm{3} \\ $$
Commented by prakash jain last updated on 10/May/20
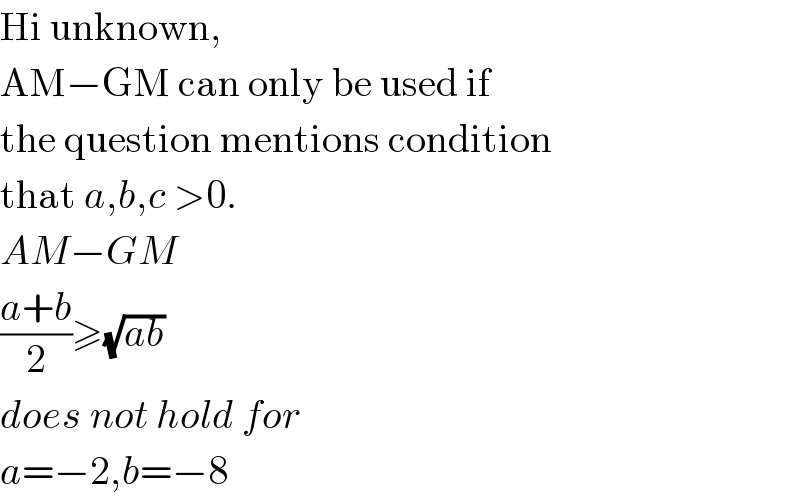
Hi unknown, AM−GM can only be used if the question mentions condition that a,b,c >0. AM−GM ((a+b)/2)≥(√(ab)) does not hold for a=−2,b=−8
$$\mathrm{Hi}\:\mathrm{unknown}, \\ $$$$\mathrm{AM}−\mathrm{GM}\:\mathrm{can}\:\mathrm{only}\:\mathrm{be}\:\mathrm{used}\:\mathrm{if} \\ $$$$\mathrm{the}\:\mathrm{question}\:\mathrm{mentions}\:\mathrm{condition} \\ $$$$\mathrm{that}\:{a},{b},{c}\:>\mathrm{0}. \\ $$$${AM}−{GM} \\ $$$$\frac{{a}+{b}}{\mathrm{2}}\geqslant\sqrt{{ab}} \\ $$$${does}\:{not}\:{hold}\:{for} \\ $$$${a}=−\mathrm{2},{b}=−\mathrm{8} \\ $$
Commented by mr W last updated on 10/May/20
i think if an extrem value (minimun or maximum) exists, it must lie on the symmetry axis. in current case at a=b=c=1 the function gets a local extrem (minimum) value. an global maximum or minimum doesn′t exist, since we see in A=2((1/a)+(1/b)+(1/c))−(a^2 +b^2 +c^2 ) A→+∞ if a or b or c →0^+ and A→−∞ if a or b or c →0^− .
$${i}\:{think}\:{if}\:{an}\:{extrem}\:{value}\:\left({minimun}\right. \\ $$$$\left.{or}\:{maximum}\right)\:{exists},\:{it}\:{must}\:{lie}\:{on} \\ $$$${the}\:{symmetry}\:{axis}.\:{in}\:{current} \\ $$$${case}\:{at}\:{a}={b}={c}=\mathrm{1}\:{the}\:{function}\:{gets} \\ $$$${a}\:{local}\:{extrem}\:\left({minimum}\right)\:{value}. \\ $$$${an}\:{global}\:{maximum}\:{or}\:{minimum}\: \\ $$$${doesn}'{t}\:{exist},\:{since}\:{we}\:{see}\:{in} \\ $$$${A}=\mathrm{2}\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right)−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$${A}\rightarrow+\infty\:{if}\:{a}\:{or}\:{b}\:{or}\:{c}\:\rightarrow\mathrm{0}^{+} \:{and} \\ $$$${A}\rightarrow−\infty\:{if}\:{a}\:{or}\:{b}\:{or}\:{c}\:\rightarrow\mathrm{0}^{−} . \\ $$
Commented by unknown last updated on 11/May/20
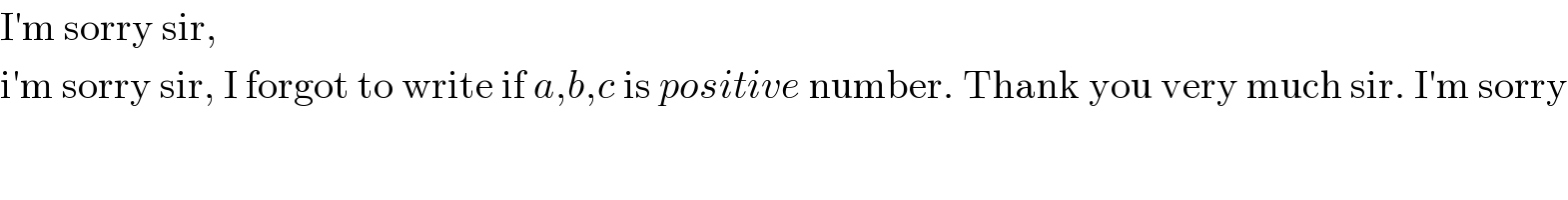
I′m sorry sir, i′m sorry sir, I forgot to write if a,b,c is positive number. Thank you very much sir. I′m sorry
$$\mathrm{I}'\mathrm{m}\:\mathrm{sorry}\:\mathrm{sir},\:\: \\ $$$$\mathrm{i}'\mathrm{m}\:\mathrm{sorry}\:\mathrm{sir},\:\mathrm{I}\:\mathrm{forgot}\:\mathrm{to}\:\mathrm{write}\:\mathrm{if}\:{a},{b},{c}\:\mathrm{is}\:{positive}\:\mathrm{number}.\:\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir}.\:\mathrm{I}'\mathrm{m}\:\mathrm{sorry} \\ $$
Commented by prakash jain last updated on 11/May/20
Ok. Have you been able to prove it usimg AM−GM or you need help?
$$\mathrm{Ok}.\:\mathrm{Have}\:\mathrm{you}\:\mathrm{been}\:\mathrm{able}\:\mathrm{to}\:\mathrm{prove} \\ $$$$\mathrm{it}\:\mathrm{usimg}\:\mathrm{AM}−\mathrm{GM}\:\mathrm{or}\:\mathrm{you}\:\mathrm{need}\:\mathrm{help}? \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *