Menu Close

find-the-number-of-values-of-p-for-which-equation-sin-3-x-1-p-3-3p-sin-x-0-p-gt-0-has-a-root-

Tinku Tara 0 Comments
Pin




Question Number 158523 by gsk2684 last updated on 05/Nov/21
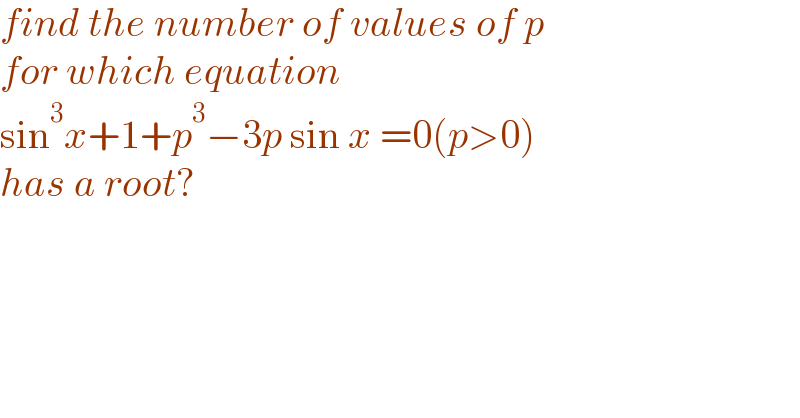
find the number of values of p for which equation sin^3 x+1+p^3 −3p sin x =0(p>0) has a root?
$${find}\:{the}\:{number}\:{of}\:{values}\:{of}\:{p} \\ $$$${for}\:{which}\:{equation}\: \\ $$$$\mathrm{sin}^{\mathrm{3}} {x}+\mathrm{1}+{p}^{\mathrm{3}} −\mathrm{3}{p}\:\mathrm{sin}\:{x}\:=\mathrm{0}\left({p}>\mathrm{0}\right) \\ $$$${has}\:{a}\:{root}? \\ $$
Answered by mr W last updated on 05/Nov/21
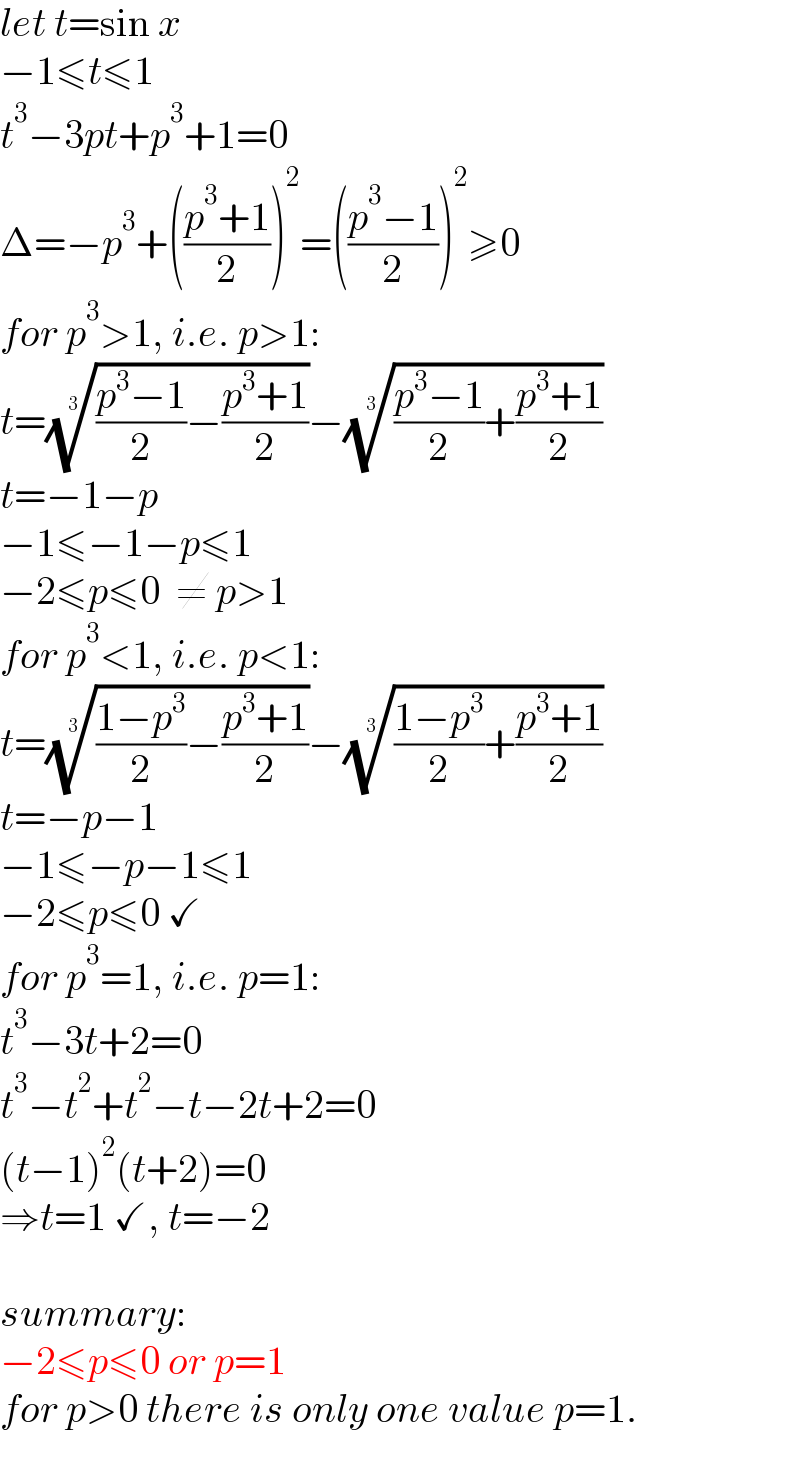
let t=sin x −1≤t≤1 t^3 −3pt+p^3 +1=0 Δ=−p^3 +(((p^3 +1)/2))^2 =(((p^3 −1)/2))^2 ≥0 for p^3 >1, i.e. p>1: t=((((p^3 −1)/2)−((p^3 +1)/2)))^(1/3) −((((p^3 −1)/2)+((p^3 +1)/2)))^(1/3) t=−1−p −1≤−1−p≤1 −2≤p≤0 ≠ p>1 for p^3 <1, i.e. p<1: t=((((1−p^3 )/2)−((p^3 +1)/2)))^(1/3) −((((1−p^3 )/2)+((p^3 +1)/2)))^(1/3) t=−p−1 −1≤−p−1≤1 −2≤p≤0 ✓ for p^3 =1, i.e. p=1: t^3 −3t+2=0 t^3 −t^2 +t^2 −t−2t+2=0 (t−1)^2 (t+2)=0 ⇒t=1 ✓, t=−2 summary: −2≤p≤0 or p=1 for p>0 there is only one value p=1.
$${let}\:{t}=\mathrm{sin}\:{x} \\ $$$$−\mathrm{1}\leqslant{t}\leqslant\mathrm{1} \\ $$$${t}^{\mathrm{3}} −\mathrm{3}{pt}+{p}^{\mathrm{3}} +\mathrm{1}=\mathrm{0} \\ $$$$\Delta=−{p}^{\mathrm{3}} +\left(\frac{{p}^{\mathrm{3}} +\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{{p}^{\mathrm{3}} −\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$${for}\:{p}^{\mathrm{3}} >\mathrm{1},\:{i}.{e}.\:{p}>\mathrm{1}: \\ $$$${t}=\sqrt[{\mathrm{3}}]{\frac{{p}^{\mathrm{3}} −\mathrm{1}}{\mathrm{2}}−\frac{{p}^{\mathrm{3}} +\mathrm{1}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\frac{{p}^{\mathrm{3}} −\mathrm{1}}{\mathrm{2}}+\frac{{p}^{\mathrm{3}} +\mathrm{1}}{\mathrm{2}}} \\ $$$${t}=−\mathrm{1}−{p} \\ $$$$−\mathrm{1}\leqslant−\mathrm{1}−{p}\leqslant\mathrm{1} \\ $$$$−\mathrm{2}\leqslant{p}\leqslant\mathrm{0}\:\:\neq\:{p}>\mathrm{1} \\ $$$${for}\:{p}^{\mathrm{3}} <\mathrm{1},\:{i}.{e}.\:{p}<\mathrm{1}: \\ $$$${t}=\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}−{p}^{\mathrm{3}} }{\mathrm{2}}−\frac{{p}^{\mathrm{3}} +\mathrm{1}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}−{p}^{\mathrm{3}} }{\mathrm{2}}+\frac{{p}^{\mathrm{3}} +\mathrm{1}}{\mathrm{2}}} \\ $$$${t}=−{p}−\mathrm{1} \\ $$$$−\mathrm{1}\leqslant−{p}−\mathrm{1}\leqslant\mathrm{1} \\ $$$$−\mathrm{2}\leqslant{p}\leqslant\mathrm{0}\:\checkmark \\ $$$${for}\:{p}^{\mathrm{3}} =\mathrm{1},\:{i}.{e}.\:{p}=\mathrm{1}: \\ $$$${t}^{\mathrm{3}} −\mathrm{3}{t}+\mathrm{2}=\mathrm{0} \\ $$$${t}^{\mathrm{3}} −{t}^{\mathrm{2}} +{t}^{\mathrm{2}} −{t}−\mathrm{2}{t}+\mathrm{2}=\mathrm{0} \\ $$$$\left({t}−\mathrm{1}\right)^{\mathrm{2}} \left({t}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{1}\:\checkmark,\:{t}=−\mathrm{2} \\ $$$$ \\ $$$${summary}: \\ $$$$−\mathrm{2}\leqslant{p}\leqslant\mathrm{0}\:{or}\:{p}=\mathrm{1} \\ $$$${for}\:{p}>\mathrm{0}\:{there}\:{is}\:{only}\:{one}\:{value}\:{p}=\mathrm{1}. \\ $$
Commented by gsk2684 last updated on 12/Nov/21
thank you sir (°⌣°)
$${thank}\:{you}\:{sir}\:\left(°\smile°\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *