Menu Close

Show-that-0-2pi-cos-3x-5-4cos-x-dx-pi-12-

Tinku Tara 0 Comments
Pin




Question Number 27464 by tawa tawa last updated on 07/Jan/18
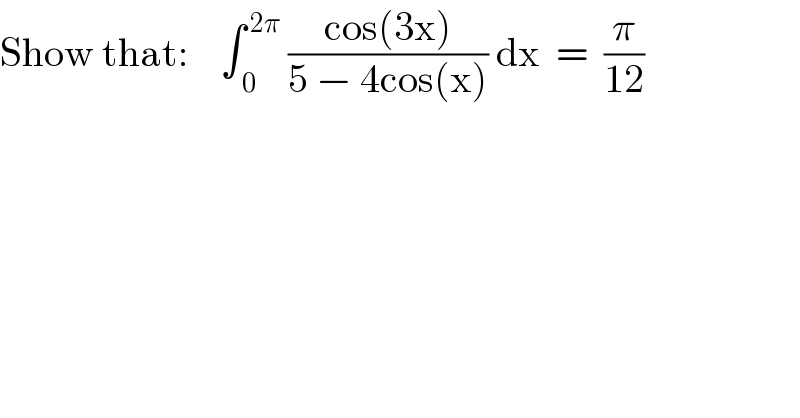
Show that: ∫_( 0) ^( 2π) ((cos(3x))/(5 − 4cos(x))) dx = (π/(12))
$$\mathrm{Show}\:\mathrm{that}:\:\:\:\:\int_{\:\mathrm{0}} ^{\:\mathrm{2}\pi} \:\frac{\mathrm{cos}\left(\mathrm{3x}\right)}{\mathrm{5}\:−\:\mathrm{4cos}\left(\mathrm{x}\right)}\:\mathrm{dx}\:\:=\:\:\frac{\pi}{\mathrm{12}} \\ $$
Commented by abdo imad last updated on 07/Jan/18
let put I= ∫_0 ^(2π) ((cos(3x))/(5−4cosx))dx and use the ch. e^(ix) =z I= ∫_(/z/=1) (((z^3 +z^(−3) )/2)/(5−4((z+z^(−1) )/2))) (dz/(iz))= (1/2)∫_(/z/=1) ((z^3 +z^(−3) )/(iz(5−2z −2z^(−1) )))dz 2I= ∫_(/z/=1) ((−i( z^3 +z^(−3) ))/(5z −2z^2 −2))dz = ∫_(/z/=1) ((i( z^3 +z^(−3) ))/(2z^2 −5z +2))dz let consider the complex function f(z) = ((i( z^3 +z^(−3) ))/(2z^2 −5z +2)) poles of f? 2z^2 −5z +2=0 Δ=25−16=9 z_1 =((5−3)/4)= (1/2) and z_2 =((5+3)/4)=2 and f(z)= ((i(z^3 +z^(−3) ))/(2(z−(1/2))(z−2))) we see that /z_(2/>1) so ∫_(/z/=1 ) f(z)dz=2iπ Res(f,(1/2)) Res(f,(1/2))= lim_(z−>(1/2)) ^ (z−(1/2))f(z)= ((i( (1/8)+8))/(2(−(3/2))))=((i((65)/8))/(−3)) =−i((65)/(24)) ⇒ ∫_(/z/=1) f(z)dz=2iπ(−i ((65)/(24)))= ((65π)/(12)) I=((65π)/(24)).
$${let}\:{put}\:{I}=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{{cos}\left(\mathrm{3}{x}\right)}{\mathrm{5}−\mathrm{4}{cosx}}{dx}\:{and}\:{use}\:{the}\:{ch}.\:{e}^{{ix}} \:={z} \\ $$$${I}=\:\int_{/{z}/=\mathrm{1}} \:\frac{\frac{{z}^{\mathrm{3}} +{z}^{−\mathrm{3}} }{\mathrm{2}}}{\mathrm{5}−\mathrm{4}\frac{{z}+{z}^{−\mathrm{1}} }{\mathrm{2}}}\:\frac{{dz}}{{iz}}=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{/{z}/=\mathrm{1}} \frac{{z}^{\mathrm{3}} +{z}^{−\mathrm{3}} }{{iz}\left(\mathrm{5}−\mathrm{2}{z}\:−\mathrm{2}{z}^{−\mathrm{1}} \right)}{dz} \\ $$$$\mathrm{2}{I}=\:\int_{/{z}/=\mathrm{1}} \frac{−{i}\left(\:{z}^{\mathrm{3}} +{z}^{−\mathrm{3}} \right)}{\mathrm{5}{z}\:−\mathrm{2}{z}^{\mathrm{2}} −\mathrm{2}}{dz}\:=\:\int_{/{z}/=\mathrm{1}} \frac{{i}\left(\:{z}^{\mathrm{3}} +{z}^{−\mathrm{3}} \right)}{\mathrm{2}{z}^{\mathrm{2}} −\mathrm{5}{z}\:+\mathrm{2}}{dz}\:{let}\:{consider} \\ $$$$ \\ $$$${the}\:{complex}\:{function}\:{f}\left({z}\right)\:=\:\frac{{i}\left(\:{z}^{\mathrm{3}} \:+{z}^{−\mathrm{3}} \right)}{\mathrm{2}{z}^{\mathrm{2}} −\mathrm{5}{z}\:+\mathrm{2}}\:\:{poles}\:{of}\:{f}? \\ $$$$\mathrm{2}{z}^{\mathrm{2}} −\mathrm{5}{z}\:+\mathrm{2}=\mathrm{0}\:\:\Delta=\mathrm{25}−\mathrm{16}=\mathrm{9} \\ $$$${z}_{\mathrm{1}} =\frac{\mathrm{5}−\mathrm{3}}{\mathrm{4}}=\:\frac{\mathrm{1}}{\mathrm{2}}\:\:{and}\:{z}_{\mathrm{2}} =\frac{\mathrm{5}+\mathrm{3}}{\mathrm{4}}=\mathrm{2}\:\:{and}\:{f}\left({z}\right)=\:\:\frac{{i}\left({z}^{\mathrm{3}} +{z}^{−\mathrm{3}} \right)}{\mathrm{2}\left({z}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left({z}−\mathrm{2}\right)} \\ $$$${we}\:{see}\:{that}\:/{z}_{\mathrm{2}/>\mathrm{1}} \:{so} \\ $$$$\int_{/{z}/=\mathrm{1}\:} {f}\left({z}\right){dz}=\mathrm{2}{i}\pi\:{Res}\left({f},\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${Res}\left({f},\frac{\mathrm{1}}{\mathrm{2}}\right)=\:{lim}_{{z}−>\frac{\mathrm{1}}{\mathrm{2}}} ^{} \left({z}−\frac{\mathrm{1}}{\mathrm{2}}\right){f}\left({z}\right)=\:\frac{{i}\left(\:\frac{\mathrm{1}}{\mathrm{8}}+\mathrm{8}\right)}{\mathrm{2}\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)}=\frac{{i}\frac{\mathrm{65}}{\mathrm{8}}}{−\mathrm{3}} \\ $$$$=−{i}\frac{\mathrm{65}}{\mathrm{24}}\:\Rightarrow\:\:\int_{/{z}/=\mathrm{1}} {f}\left({z}\right){dz}=\mathrm{2}{i}\pi\left(−{i}\:\frac{\mathrm{65}}{\mathrm{24}}\right)=\:\frac{\mathrm{65}\pi}{\mathrm{12}} \\ $$$${I}=\frac{\mathrm{65}\pi}{\mathrm{24}}. \\ $$$$ \\ $$
Commented by abdo imad last updated on 07/Jan/18
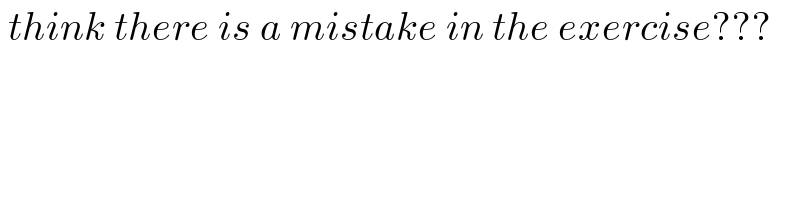
think there is a mistake in the exercise???
$$\:{think}\:{there}\:{is}\:{a}\:{mistake}\:{in}\:{the}\:{exercise}??? \\ $$
Commented by tawa tawa last updated on 07/Jan/18
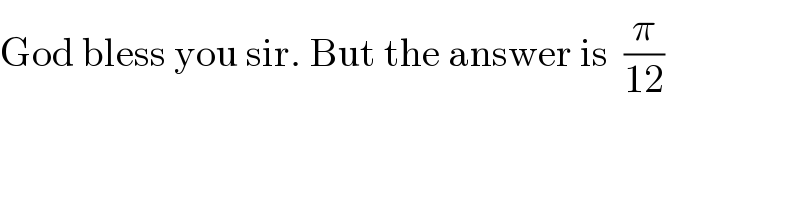
God bless you sir. But the answer is (π/(12))
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{But}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\:\frac{\pi}{\mathrm{12}} \\ $$
Commented by abdo imad last updated on 07/Jan/18
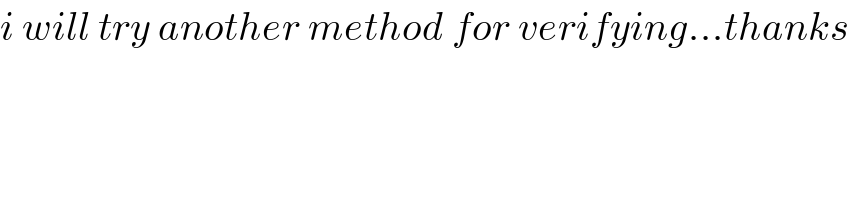
i will try another method for verifying...thanks
$${i}\:{will}\:{try}\:{another}\:{method}\:{for}\:{verifying}…{thanks} \\ $$
Commented by tawa tawa last updated on 07/Jan/18
I really appreciate sir. God bless you
$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *