Question Number 27503 by Rasheed.Sindhi last updated on 07/Jan/18
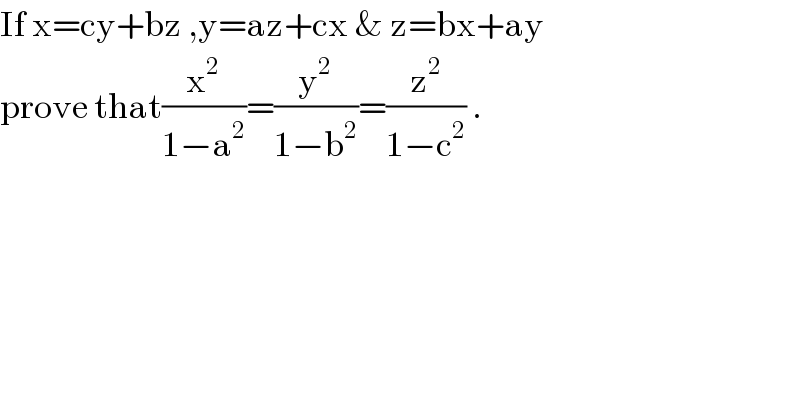
$$\mathrm{If}\:\mathrm{x}=\mathrm{cy}+\mathrm{bz}\:,\mathrm{y}=\mathrm{az}+\mathrm{cx}\:\&\:\mathrm{z}=\mathrm{bx}+\mathrm{ay} \\ $$$$\mathrm{prove}\:\mathrm{that}\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }=\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{1}−\mathrm{b}^{\mathrm{2}} }=\frac{\mathrm{z}^{\mathrm{2}} }{\mathrm{1}−\mathrm{c}^{\mathrm{2}} }\:. \\ $$
Answered by mrW1 last updated on 07/Jan/18
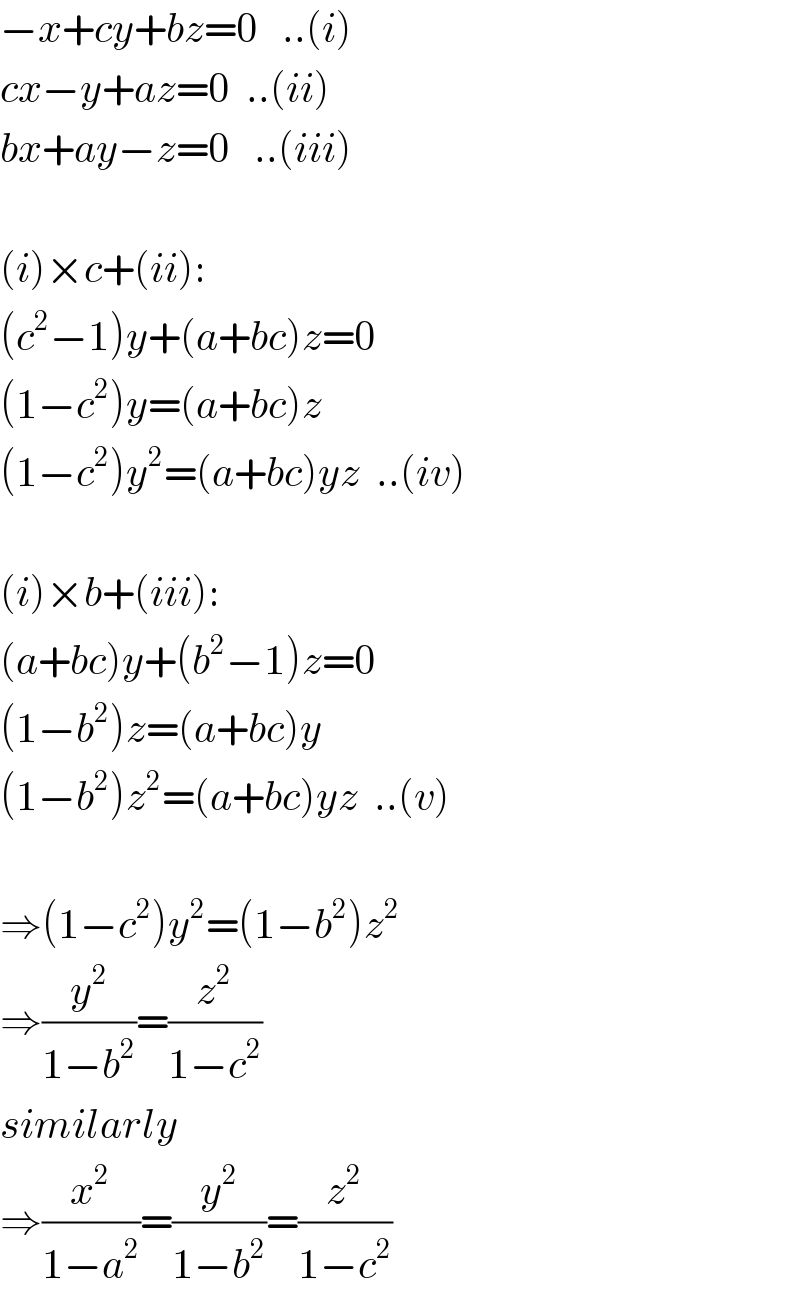
$$−{x}+{cy}+{bz}=\mathrm{0}\:\:\:..\left({i}\right) \\ $$$${cx}−{y}+{az}=\mathrm{0}\:\:..\left({ii}\right) \\ $$$${bx}+{ay}−{z}=\mathrm{0}\:\:\:..\left({iii}\right) \\ $$$$ \\ $$$$\left({i}\right)×{c}+\left({ii}\right): \\ $$$$\left({c}^{\mathrm{2}} −\mathrm{1}\right){y}+\left({a}+{bc}\right){z}=\mathrm{0} \\ $$$$\left(\mathrm{1}−{c}^{\mathrm{2}} \right){y}=\left({a}+{bc}\right){z} \\ $$$$\left(\mathrm{1}−{c}^{\mathrm{2}} \right){y}^{\mathrm{2}} =\left({a}+{bc}\right){yz}\:\:..\left({iv}\right) \\ $$$$ \\ $$$$\left({i}\right)×{b}+\left({iii}\right): \\ $$$$\left({a}+{bc}\right){y}+\left({b}^{\mathrm{2}} −\mathrm{1}\right){z}=\mathrm{0} \\ $$$$\left(\mathrm{1}−{b}^{\mathrm{2}} \right){z}=\left({a}+{bc}\right){y} \\ $$$$\left(\mathrm{1}−{b}^{\mathrm{2}} \right){z}^{\mathrm{2}} =\left({a}+{bc}\right){yz}\:\:..\left({v}\right) \\ $$$$ \\ $$$$\Rightarrow\left(\mathrm{1}−{c}^{\mathrm{2}} \right){y}^{\mathrm{2}} =\left(\mathrm{1}−{b}^{\mathrm{2}} \right){z}^{\mathrm{2}} \\ $$$$\Rightarrow\frac{{y}^{\mathrm{2}} }{\mathrm{1}−{b}^{\mathrm{2}} }=\frac{{z}^{\mathrm{2}} }{\mathrm{1}−{c}^{\mathrm{2}} } \\ $$$${similarly} \\ $$$$\Rightarrow\frac{{x}^{\mathrm{2}} }{\mathrm{1}−{a}^{\mathrm{2}} }=\frac{{y}^{\mathrm{2}} }{\mathrm{1}−{b}^{\mathrm{2}} }=\frac{{z}^{\mathrm{2}} }{\mathrm{1}−{c}^{\mathrm{2}} } \\ $$
Commented by Rasheed.Sindhi last updated on 07/Jan/18

$$\mathcal{WELDONE}\:\:\mathcal{S}{i}\mathcal{R}! \\ $$
