Question Number 158598 by HongKing last updated on 06/Nov/21

Commented by MJS_new last updated on 06/Nov/21
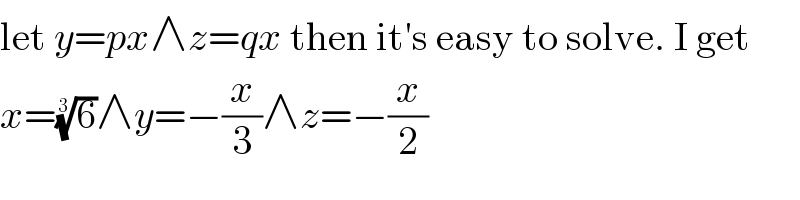
$$\mathrm{let}\:{y}={px}\wedge{z}={qx}\:\mathrm{then}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve}.\:\mathrm{I}\:\mathrm{get} \\ $$$${x}=\sqrt[{\mathrm{3}}]{\mathrm{6}}\wedge{y}=−\frac{{x}}{\mathrm{3}}\wedge{z}=−\frac{{x}}{\mathrm{2}} \\ $$
Commented by HongKing last updated on 06/Nov/21

$$\mathrm{Yes}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Ser} \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{interested}\:\mathrm{in}\:\mathrm{you}\:\mathrm{creative}\:\mathrm{solution} \\ $$$$\mathrm{if}\:\mathrm{possible}\:\mathrm{please} \\ $$
Answered by Rasheed.Sindhi last updated on 06/Nov/21

$${What}'{s}\:{wrong}\:{in}\:{the}\:{following}\:{process}: \\ $$$$\begin{cases}{−{x}^{\mathrm{2}} \left({y}−{z}\right)=−\mathrm{1}}\\{{y}^{\mathrm{2}} \left({z}−{x}\right)=−\mathrm{1}}\\{{z}^{\mathrm{2}} \left({x}−{y}\right)=\mathrm{2}}\end{cases} \\ $$$${Adding}\:{all}\:{the}\:{three}: \\ $$$$−{x}^{\mathrm{2}} \left({y}−{z}\right)+{y}^{\mathrm{2}} \left({z}−{x}\right)+{z}^{\mathrm{2}} \left({x}−{y}\right)=\mathrm{0} \\ $$$$\left({y}−{z}\right)\left(−{x}^{\mathrm{2}} −{xy}+{yz}−{zx}\right)=\mathrm{0} \\ $$$${y}−{z}=\mathrm{0}\:\mid\:−{x}^{\mathrm{2}} −{xy}+{yz}−{zx}=\mathrm{0} \\ $$$${y}={z}\:???????????????? \\ $$$$\boldsymbol{\mathrm{O}}\mathrm{bviously}\:\mathrm{false}! \\ $$
Commented by HongKing last updated on 07/Nov/21

$$\mathrm{how}\:\mathrm{my}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$
Commented by mr W last updated on 07/Nov/21
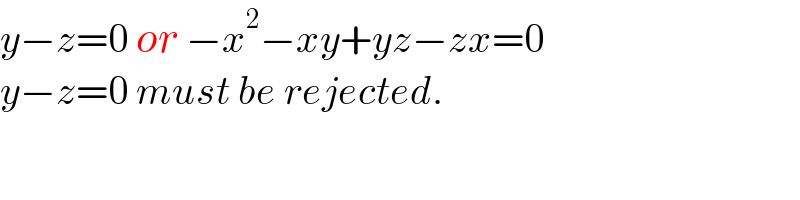
$${y}−{z}=\mathrm{0}\:{or}\:−{x}^{\mathrm{2}} −{xy}+{yz}−{zx}=\mathrm{0} \\ $$$${y}−{z}=\mathrm{0}\:{must}\:{be}\:{rejected}. \\ $$
Commented by Rasheed.Sindhi last updated on 07/Nov/21
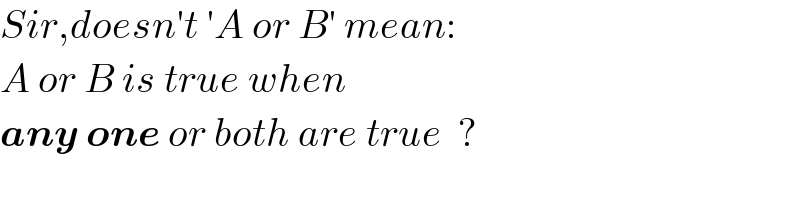
$${Sir},{doesn}'{t}\:'{A}\:{or}\:{B}'\:{mean}: \\ $$$${A}\:{or}\:{B}\:{is}\:{true}\:{when} \\ $$$$\boldsymbol{{any}}\:\boldsymbol{{one}}\:{or}\:{both}\:{are}\:{true}\:\:? \\ $$
Commented by mr W last updated on 07/Nov/21
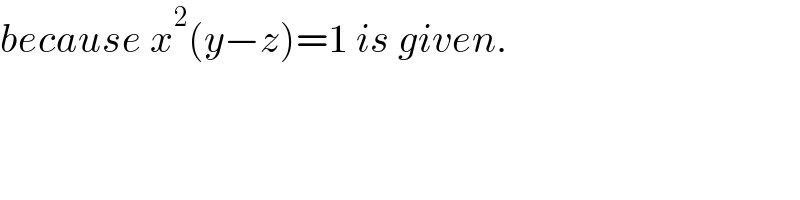
$${because}\:{x}^{\mathrm{2}} \left({y}−{z}\right)=\mathrm{1}\:{is}\:{given}. \\ $$
Commented by Rasheed.Sindhi last updated on 07/Nov/21

$${Gratefull}\:{Sir}! \\ $$
Commented by mr W last updated on 07/Nov/21
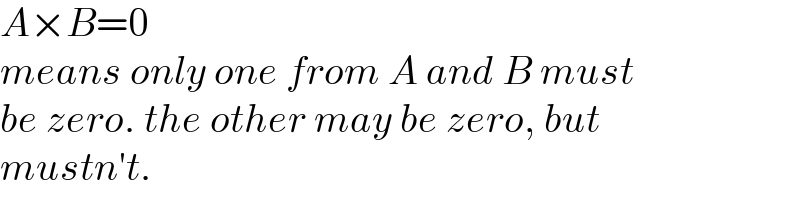
$${A}×{B}=\mathrm{0} \\ $$$${means}\:{only}\:{one}\:{from}\:{A}\:{and}\:{B}\:{must} \\ $$$${be}\:{zero}.\:{the}\:{other}\:{may}\:{be}\:{zero},\:{but} \\ $$$${mustn}'{t}. \\ $$
Commented by Rasheed.Sindhi last updated on 07/Nov/21

$${Sir},\:{then}\:{why}\:{is}\:\:{y}−{z}=\mathrm{0}\:\:{rejected}? \\ $$
Answered by mr W last updated on 06/Nov/21
![((y^2 (z−x))/(x^2 (y−z)))=−1 ((y/x))^2 (((z/x)−1)/((y/x)−(z/x)))=−1 let p=(y/x), q=(z/x) p^2 (q−1)=−(p−q) (p−1)[(p+1)q−p]=0 ...(i) ((z^2 (x−y))/(x^2 (y−z)))=2 ((z/x))^2 ((1−(y/x))/((y/x)−(z/x)))=2 q^2 (1−p)=2(p−q) q(q+2)=(2+q^2 )p p=((q(q+2))/(2+q^2 )) ...(ii) case 1: from (i): p=1 from (ii): q=1 ⇒no solution case 2: from (i): (p+1)q−p=0 ⇒p=(q/(1−q)) ((q(q+2))/(2+q^2 ))=(q/(1−q)) q≠0 ((q+2)/(2+q^2 ))=(1/(1−q)) 2q^2 +q=0 2q+1=0 ⇒q=−(1/2) ⇒p=((−(1/2))/(1+(1/2)))=−(1/3) x^2 (−(x/3)+(x/2))=1 (x^3 /6)=1 ⇒x=(6)^(1/3) ⇒y=−((6)^(1/3) /3) ⇒z=−((6)^(1/3) /2)](https://www.tinkutara.com/question/Q158612.png)
$$\frac{{y}^{\mathrm{2}} \left({z}−{x}\right)}{{x}^{\mathrm{2}} \left({y}−{z}\right)}=−\mathrm{1} \\ $$$$\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} \frac{\frac{{z}}{{x}}−\mathrm{1}}{\frac{{y}}{{x}}−\frac{{z}}{{x}}}=−\mathrm{1} \\ $$$${let}\:{p}=\frac{{y}}{{x}},\:{q}=\frac{{z}}{{x}} \\ $$$${p}^{\mathrm{2}} \left({q}−\mathrm{1}\right)=−\left({p}−{q}\right) \\ $$$$\left({p}−\mathrm{1}\right)\left[\left({p}+\mathrm{1}\right){q}−{p}\right]=\mathrm{0}\:\:\:…\left({i}\right) \\ $$$$\frac{{z}^{\mathrm{2}} \left({x}−{y}\right)}{{x}^{\mathrm{2}} \left({y}−{z}\right)}=\mathrm{2} \\ $$$$\left(\frac{{z}}{{x}}\right)^{\mathrm{2}} \frac{\mathrm{1}−\frac{{y}}{{x}}}{\frac{{y}}{{x}}−\frac{{z}}{{x}}}=\mathrm{2} \\ $$$${q}^{\mathrm{2}} \left(\mathrm{1}−{p}\right)=\mathrm{2}\left({p}−{q}\right) \\ $$$${q}\left({q}+\mathrm{2}\right)=\left(\mathrm{2}+{q}^{\mathrm{2}} \right){p} \\ $$$${p}=\frac{{q}\left({q}+\mathrm{2}\right)}{\mathrm{2}+{q}^{\mathrm{2}} }\:\:\:…\left({ii}\right) \\ $$$${case}\:\mathrm{1}: \\ $$$${from}\:\left({i}\right):\:{p}=\mathrm{1} \\ $$$${from}\:\left({ii}\right):\:{q}=\mathrm{1} \\ $$$$\Rightarrow{no}\:{solution} \\ $$$${case}\:\mathrm{2}: \\ $$$${from}\:\left({i}\right):\:\left({p}+\mathrm{1}\right){q}−{p}=\mathrm{0}\:\Rightarrow{p}=\frac{{q}}{\mathrm{1}−{q}} \\ $$$$\frac{{q}\left({q}+\mathrm{2}\right)}{\mathrm{2}+{q}^{\mathrm{2}} }=\frac{{q}}{\mathrm{1}−{q}} \\ $$$${q}\neq\mathrm{0} \\ $$$$\frac{{q}+\mathrm{2}}{\mathrm{2}+{q}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{1}−{q}} \\ $$$$\mathrm{2}{q}^{\mathrm{2}} +{q}=\mathrm{0} \\ $$$$\mathrm{2}{q}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{q}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{p}=\frac{−\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}}=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${x}^{\mathrm{2}} \left(−\frac{{x}}{\mathrm{3}}+\frac{{x}}{\mathrm{2}}\right)=\mathrm{1} \\ $$$$\frac{{x}^{\mathrm{3}} }{\mathrm{6}}=\mathrm{1} \\ $$$$\Rightarrow{x}=\sqrt[{\mathrm{3}}]{\mathrm{6}} \\ $$$$\Rightarrow{y}=−\frac{\sqrt[{\mathrm{3}}]{\mathrm{6}}}{\mathrm{3}} \\ $$$$\Rightarrow{z}=−\frac{\sqrt[{\mathrm{3}}]{\mathrm{6}}}{\mathrm{2}} \\ $$
Commented by HongKing last updated on 07/Nov/21
$$\mathrm{perfect}\:\mathrm{my}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much} \\ $$
Commented by Tawa11 last updated on 07/Nov/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
