Menu Close

Question-158622

Tinku Tara 0 Comments
Pin




Question Number 158622 by ajfour last updated on 06/Nov/21
Commented by ajfour last updated on 06/Nov/21
Find maximum side length of inscribed square (s_(max) ).
$${Find}\:{maximum}\:{side}\:{length} \\ $$$${of}\:{inscribed}\:{square}\:\left({s}_{{max}} \right). \\ $$
Answered by mr W last updated on 07/Nov/21
Commented by mr W last updated on 07/Nov/21
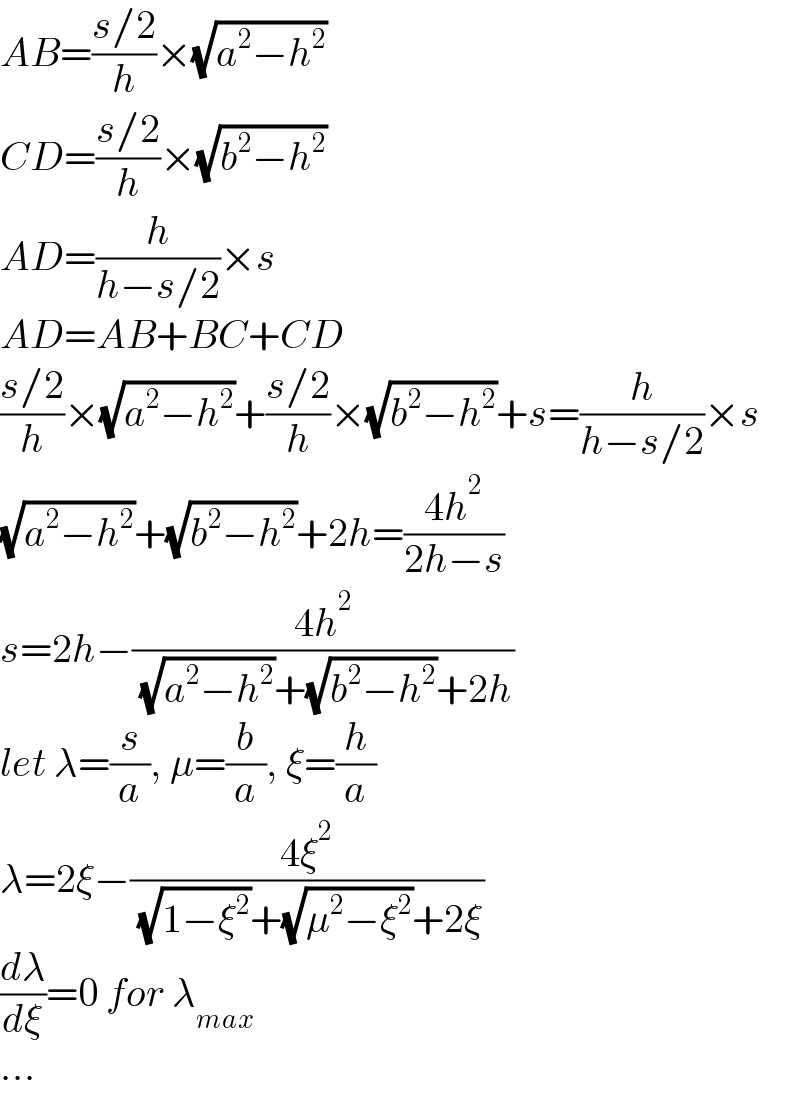
AB=((s/2)/h)×(√(a^2 −h^2 )) CD=((s/2)/h)×(√(b^2 −h^2 )) AD=(h/(h−s/2))×s AD=AB+BC+CD ((s/2)/h)×(√(a^2 −h^2 ))+((s/2)/h)×(√(b^2 −h^2 ))+s=(h/(h−s/2))×s (√(a^2 −h^2 ))+(√(b^2 −h^2 ))+2h=((4h^2 )/(2h−s)) s=2h−((4h^2 )/( (√(a^2 −h^2 ))+(√(b^2 −h^2 ))+2h)) let λ=(s/a), μ=(b/a), ξ=(h/a) λ=2ξ−((4ξ^2 )/( (√(1−ξ^2 ))+(√(μ^2 −ξ^2 ))+2ξ)) (dλ/dξ)=0 for λ_(max) ...
$${AB}=\frac{{s}/\mathrm{2}}{{h}}×\sqrt{{a}^{\mathrm{2}} −{h}^{\mathrm{2}} } \\ $$$${CD}=\frac{{s}/\mathrm{2}}{{h}}×\sqrt{{b}^{\mathrm{2}} −{h}^{\mathrm{2}} } \\ $$$${AD}=\frac{{h}}{{h}−{s}/\mathrm{2}}×{s} \\ $$$${AD}={AB}+{BC}+{CD} \\ $$$$\frac{{s}/\mathrm{2}}{{h}}×\sqrt{{a}^{\mathrm{2}} −{h}^{\mathrm{2}} }+\frac{{s}/\mathrm{2}}{{h}}×\sqrt{{b}^{\mathrm{2}} −{h}^{\mathrm{2}} }+{s}=\frac{{h}}{{h}−{s}/\mathrm{2}}×{s} \\ $$$$\sqrt{{a}^{\mathrm{2}} −{h}^{\mathrm{2}} }+\sqrt{{b}^{\mathrm{2}} −{h}^{\mathrm{2}} }+\mathrm{2}{h}=\frac{\mathrm{4}{h}^{\mathrm{2}} }{\mathrm{2}{h}−{s}} \\ $$$${s}=\mathrm{2}{h}−\frac{\mathrm{4}{h}^{\mathrm{2}} }{\:\sqrt{{a}^{\mathrm{2}} −{h}^{\mathrm{2}} }+\sqrt{{b}^{\mathrm{2}} −{h}^{\mathrm{2}} }+\mathrm{2}{h}} \\ $$$${let}\:\lambda=\frac{{s}}{{a}},\:\mu=\frac{{b}}{{a}},\:\xi=\frac{{h}}{{a}} \\ $$$$\lambda=\mathrm{2}\xi−\frac{\mathrm{4}\xi^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−\xi^{\mathrm{2}} }+\sqrt{\mu^{\mathrm{2}} −\xi^{\mathrm{2}} }+\mathrm{2}\xi} \\ $$$$\frac{{d}\lambda}{{d}\xi}=\mathrm{0}\:{for}\:\lambda_{{max}} \\ $$$$… \\ $$
Commented by mr W last updated on 07/Nov/21
Commented by ajfour last updated on 07/Nov/21
Thank you sir. I′ll think of some better elliptic way.
$$\mathbb{T}\mathrm{hank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}'\mathrm{ll}\:\mathrm{think}\:\mathrm{of} \\ $$$$\mathrm{some}\:\mathrm{better}\:\mathrm{elliptic}\:\mathrm{way}. \\ $$
Commented by ajfour last updated on 07/Nov/21
s^2 =h(√(a^2 −h^2 ))+h(√(b^2 −h^2 )) −{(s/2)p+(s/2)q+s(h−(s/2))} p+q+s=(√(a^2 −h^2 ))+(√(b^2 −h^2 )) ⇒ hs=(h+(s/2))((√(a^2 −h^2 ))+(√(b^2 −h^2 ))) ⇒ (1/s)=(1/( (√(a^2 −h^2 ))+(√(b^2 −h^2 ))))−(1/(2h)) ...............
$${s}^{\mathrm{2}} ={h}\sqrt{{a}^{\mathrm{2}} −{h}^{\mathrm{2}} }+{h}\sqrt{{b}^{\mathrm{2}} −{h}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:−\left\{\frac{{s}}{\mathrm{2}}{p}+\frac{{s}}{\mathrm{2}}{q}+{s}\left({h}−\frac{{s}}{\mathrm{2}}\right)\right\} \\ $$$${p}+{q}+{s}=\sqrt{{a}^{\mathrm{2}} −{h}^{\mathrm{2}} }+\sqrt{{b}^{\mathrm{2}} −{h}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:{hs}=\left({h}+\frac{{s}}{\mathrm{2}}\right)\left(\sqrt{{a}^{\mathrm{2}} −{h}^{\mathrm{2}} }+\sqrt{{b}^{\mathrm{2}} −{h}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow \\ $$$$\:\frac{\mathrm{1}}{\boldsymbol{{s}}}=\frac{\mathrm{1}}{\:\sqrt{\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{h}}^{\mathrm{2}} }+\sqrt{\boldsymbol{{b}}^{\mathrm{2}} −\boldsymbol{{h}}^{\mathrm{2}} }}−\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{h}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…………… \\ $$
Commented by Tawa11 last updated on 07/Nov/21
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *