Question Number 2489 by Filup last updated on 21/Nov/15
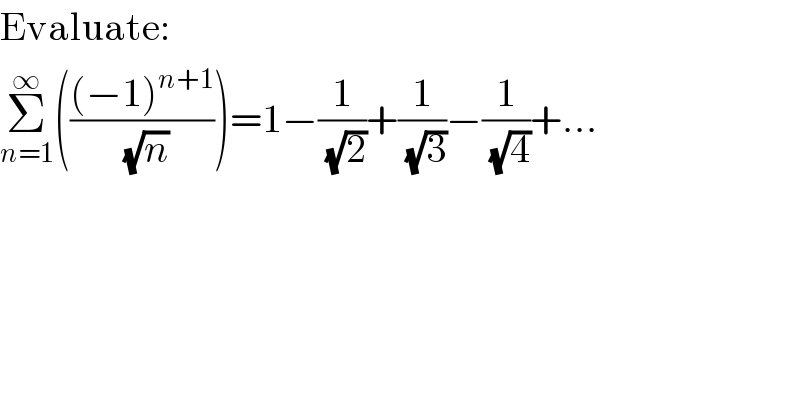
$$\mathrm{Evaluate}: \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\:\sqrt{{n}}}\right)=\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}}}+… \\ $$
Commented by Yozzi last updated on 21/Nov/15
![Σ_(r=1) ^∞ (((−1)^(r+1) )/( (√n)))=Σ_(r=1) ^∞ (1/( (√(2r−1))))−Σ_(r=1) ^∞ (1/( (√(2r)))) Let f(x)=(2x−1)^(−1/2) . f is decreasing and positive for x≥1 so the integral test could show whether Σ_(r=1) ^∞ (1/( (√(2r−1)))) is convergent or not. Let I=∫_1 ^∞ f(x)dx=lim_(m→∞) ∫_1 ^m (2x−1)^(−1/2) dx I=lim_(m→∞) ((((2x−1)^(1/2) )/(2×1/2)))∣_1 ^m I=lim_(m→∞) [(√(2m−1))−(√(2×1−1))] I=lim_(m→∞) [(√(2m−1))−1]=(√(2×∞−1))−1=∞ Thus,since I does not exist,Σ_(r=1) ^∞ (1/( (√(2r−1)))) is divergent. {Hence, Σ_(r=1) ^∞ (((−1)^(n+1) )/( (√n))) is divergent.} (×)](https://www.tinkutara.com/question/Q2494.png)
$$\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{r}+\mathrm{1}} }{\:\sqrt{{n}}}=\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{r}−\mathrm{1}}}−\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{r}}} \\ $$$${Let}\:{f}\left({x}\right)=\left(\mathrm{2}{x}−\mathrm{1}\right)^{−\mathrm{1}/\mathrm{2}} .\:{f}\:{is}\:{decreasing} \\ $$$${and}\:{positive}\:{for}\:{x}\geqslant\mathrm{1}\:{so}\:{the}\:{integral} \\ $$$${test}\:{could}\:{show}\:{whether}\:\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{r}−\mathrm{1}}}\:{is} \\ $$$${convergent}\:{or}\:{not}. \\ $$$${Let}\:{I}=\int_{\mathrm{1}} ^{\infty} {f}\left({x}\right){dx}=\underset{{m}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{1}} ^{{m}} \left(\mathrm{2}{x}−\mathrm{1}\right)^{−\mathrm{1}/\mathrm{2}} {dx} \\ $$$${I}=\underset{{m}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{1}/\mathrm{2}} }{\mathrm{2}×\mathrm{1}/\mathrm{2}}\right)\mid_{\mathrm{1}} ^{{m}} \\ $$$${I}=\underset{{m}\rightarrow\infty} {\mathrm{lim}}\left[\sqrt{\mathrm{2}{m}−\mathrm{1}}−\sqrt{\mathrm{2}×\mathrm{1}−\mathrm{1}}\right] \\ $$$${I}=\underset{{m}\rightarrow\infty} {\mathrm{lim}}\left[\sqrt{\mathrm{2}{m}−\mathrm{1}}−\mathrm{1}\right]=\sqrt{\mathrm{2}×\infty−\mathrm{1}}−\mathrm{1}=\infty \\ $$$${Thus},{since}\:{I}\:{does}\:{not}\:{exist},\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{r}−\mathrm{1}}} \\ $$$${is}\:{divergent}.\: \\ $$$$\left\{{Hence},\:\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\:\sqrt{{n}}}\:{is}\:{divergent}.\right\}\:\left(×\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by Yozzi last updated on 21/Nov/15

$$\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\:\sqrt{{n}}}\right)\:{does}\:{not}\:{converge}. \\ $$$$\left({Incorrect}−{disregard}\:{this}\:{contribution}\right). \\ $$
Commented by prakash jain last updated on 21/Nov/15

$$\mathrm{The}\:\mathrm{sequence}\:\mathrm{may}\:\mathrm{be}\:\mathrm{conditinally}\:\mathrm{convergent}. \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{tests}\:\mathrm{in}\:\mathrm{comment}\:\mathrm{only}\:\mathrm{prove} \\ $$$$\mathrm{that}\:\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{absolutely}\:\mathrm{convergent}. \\ $$
Commented by 123456 last updated on 21/Nov/15

$$\mathrm{0}<{a}_{{n}+\mathrm{1}} <{a}_{{n}} \:\left(\mathrm{by}\:\mathrm{alternating}\:\mathrm{test}\:\mathrm{it}\:\mathrm{converge}\right) \\ $$$$\mathrm{its}\:\mathrm{coditionly}\:\mathrm{converge}\:\mathrm{since} \\ $$$$\Sigma\mathrm{1}/\sqrt{{n}} \\ $$$$\mathrm{diverge}\:\mathrm{by}\:{p}\:\mathrm{series}\:\mathrm{test} \\ $$
Answered by prakash jain last updated on 21/Nov/15

$$\eta\left({s}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{{s}} }\:\:\:\left(\mathrm{Dirichlet}\:\mathrm{eta}\:\mathrm{function}\right) \\ $$$$\mathrm{The}\:\mathrm{given}\:\mathrm{series}=\eta\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$
