Question Number 27608 by chernoaguero@gmail.com last updated on 10/Jan/18
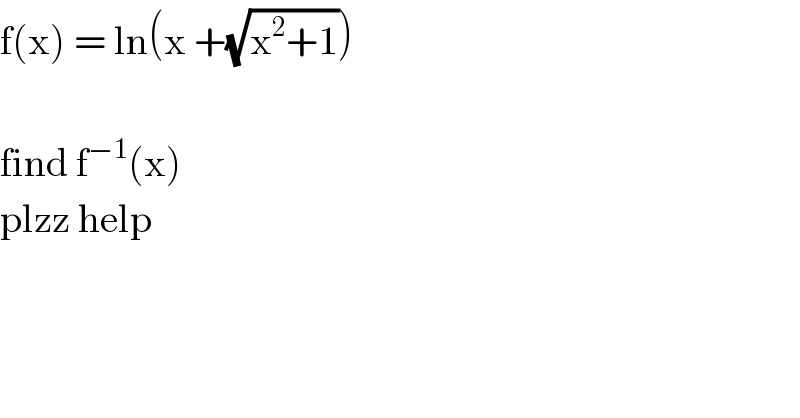
$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{ln}\left(\mathrm{x}\:+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$$ \\ $$$$\mathrm{find}\:\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right) \\ $$$$\mathrm{plzz}\:\mathrm{help} \\ $$
Commented by abdo imad last updated on 11/Jan/18
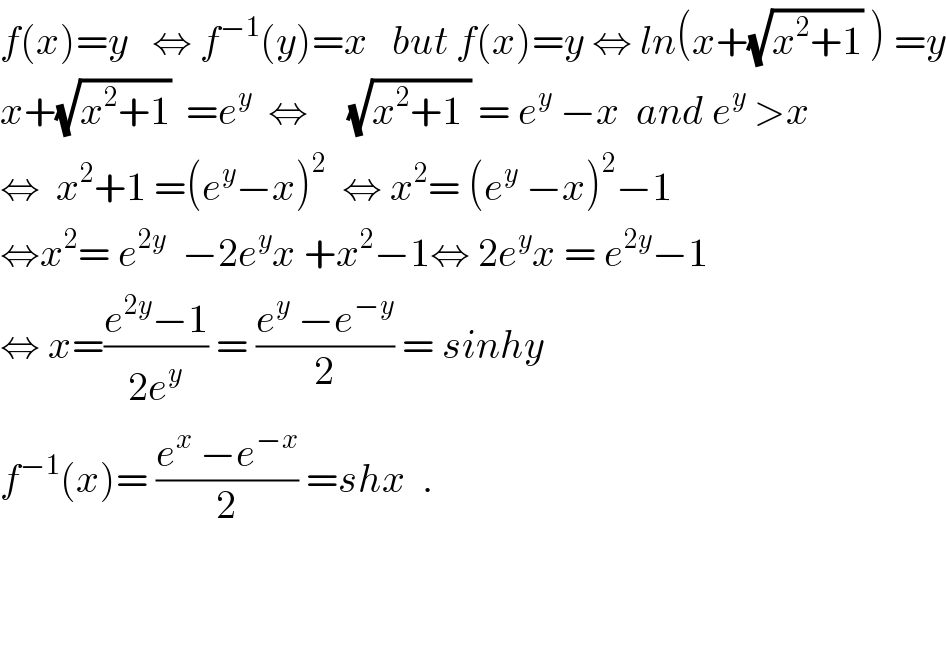
$${f}\left({x}\right)={y}\:\:\:\Leftrightarrow\:{f}^{−\mathrm{1}} \left({y}\right)={x}\:\:\:{but}\:{f}\left({x}\right)={y}\:\Leftrightarrow\:{ln}\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\right)\:={y} \\ $$$${x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\:={e}^{{y}} \:\:\Leftrightarrow\:\:\:\:\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}\:}\:=\:{e}^{{y}} \:−{x}\:\:{and}\:{e}^{{y}} \:>{x} \\ $$$$\Leftrightarrow\:\:{x}^{\mathrm{2}} +\mathrm{1}\:=\left({e}^{{y}} −{x}\right)^{\mathrm{2}} \:\:\Leftrightarrow\:{x}^{\mathrm{2}} =\:\left({e}^{{y}} \:−{x}\right)^{\mathrm{2}} −\mathrm{1} \\ $$$$\Leftrightarrow{x}^{\mathrm{2}} =\:{e}^{\mathrm{2}{y}} \:\:−\mathrm{2}{e}^{{y}} {x}\:+{x}^{\mathrm{2}} −\mathrm{1}\Leftrightarrow\:\mathrm{2}{e}^{{y}} {x}\:=\:{e}^{\mathrm{2}{y}} −\mathrm{1} \\ $$$$\Leftrightarrow\:{x}=\frac{{e}^{\mathrm{2}{y}} −\mathrm{1}}{\mathrm{2}{e}^{{y}} }\:=\:\frac{{e}^{{y}} \:−{e}^{−{y}} }{\mathrm{2}}\:=\:{sinhy} \\ $$$${f}^{−\mathrm{1}} \left({x}\right)=\:\frac{{e}^{{x}} \:−{e}^{−{x}} }{\mathrm{2}}\:={shx}\:\:. \\ $$$$ \\ $$$$ \\ $$
Commented by chernoaguero@gmail.com last updated on 11/Jan/18
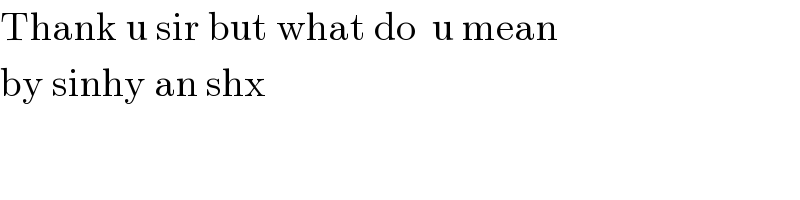
$$\mathrm{Thank}\:\mathrm{u}\:\mathrm{sir}\:\mathrm{but}\:\mathrm{what}\:\mathrm{do}\:\:\mathrm{u}\:\mathrm{mean} \\ $$$$\mathrm{by}\:\mathrm{sinhy}\:\mathrm{an}\:\mathrm{shx} \\ $$
Commented by Joel578 last updated on 11/Jan/18

$$\mathrm{sh}\:{x}\:\mathrm{is}\:\mathrm{sinh}\:{x} \\ $$
Commented by abdo imad last updated on 11/Jan/18

$${sinhx}={shx}\:{its}\:{only}\:{a}\:{notation}. \\ $$
Commented by chernoaguero@gmail.com last updated on 11/Jan/18

$$\mathrm{ok}\:\mathrm{thank}\: \\ $$
