Question Number 158699 by MathsFan last updated on 07/Nov/21
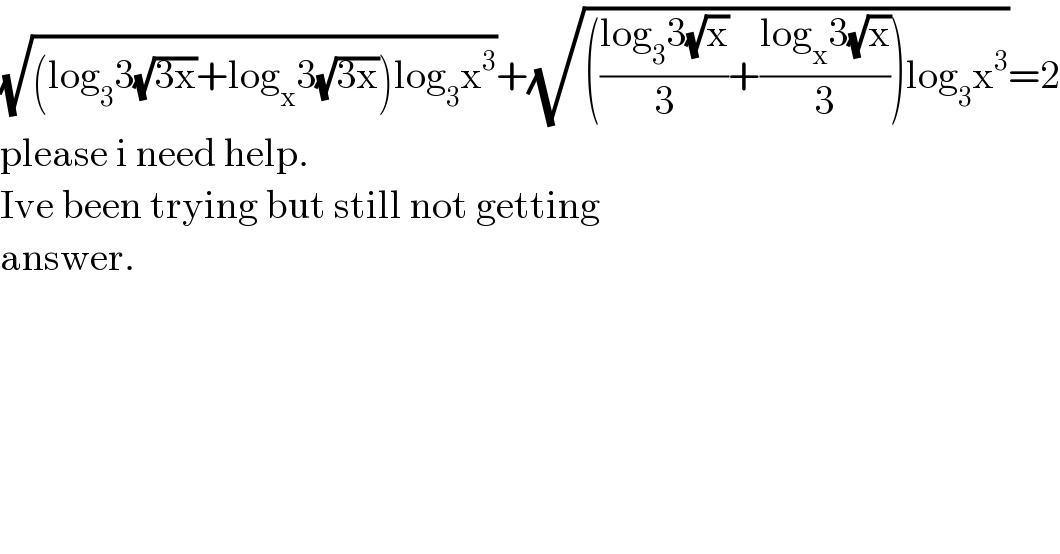
$$\sqrt{\left(\mathrm{log}_{\mathrm{3}} \mathrm{3}\sqrt{\mathrm{3x}}+\mathrm{log}_{\mathrm{x}} \mathrm{3}\sqrt{\mathrm{3x}}\right)\mathrm{log}_{\mathrm{3}} \mathrm{x}^{\mathrm{3}} }+\sqrt{\left(\frac{\mathrm{log}_{\mathrm{3}} \mathrm{3}\sqrt{\mathrm{x}}}{\mathrm{3}}+\frac{\mathrm{log}_{\mathrm{x}} \mathrm{3}\sqrt{\mathrm{x}}}{\mathrm{3}}\right)\mathrm{log}_{\mathrm{3}} \mathrm{x}^{\mathrm{3}} }=\mathrm{2} \\ $$$$\mathrm{please}\:\mathrm{i}\:\mathrm{need}\:\mathrm{help}. \\ $$$$\mathrm{Ive}\:\mathrm{been}\:\mathrm{trying}\:\mathrm{but}\:\mathrm{still}\:\mathrm{not}\:\mathrm{getting}\: \\ $$$$\mathrm{answer}. \\ $$
Commented by MJS_new last updated on 08/Nov/21
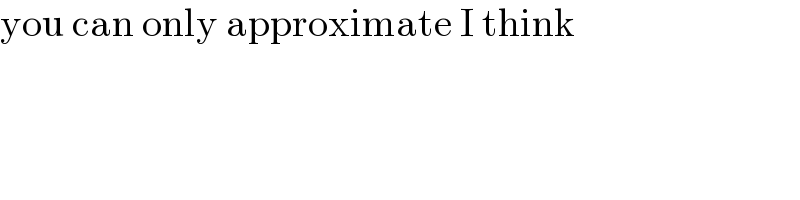
$$\mathrm{you}\:\mathrm{can}\:\mathrm{only}\:\mathrm{approximate}\:\mathrm{I}\:\mathrm{think} \\ $$
Commented by MJS_new last updated on 08/Nov/21
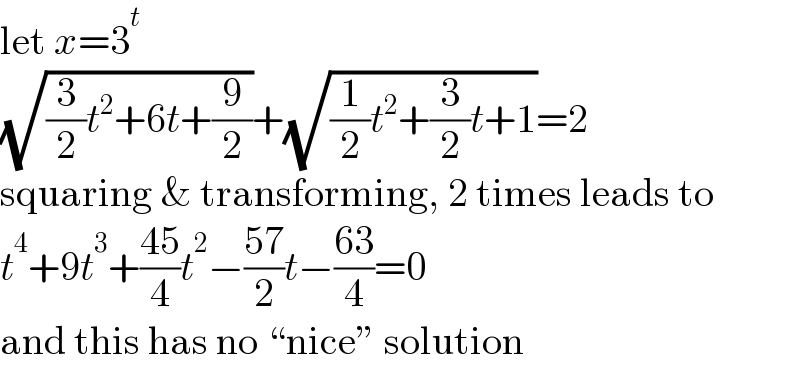
$$\mathrm{let}\:{x}=\mathrm{3}^{{t}} \\ $$$$\sqrt{\frac{\mathrm{3}}{\mathrm{2}}{t}^{\mathrm{2}} +\mathrm{6}{t}+\frac{\mathrm{9}}{\mathrm{2}}}+\sqrt{\frac{\mathrm{1}}{\mathrm{2}}{t}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}{t}+\mathrm{1}}=\mathrm{2} \\ $$$$\mathrm{squaring}\:\&\:\mathrm{transforming},\:\mathrm{2}\:\mathrm{times}\:\mathrm{leads}\:\mathrm{to} \\ $$$${t}^{\mathrm{4}} +\mathrm{9}{t}^{\mathrm{3}} +\frac{\mathrm{45}}{\mathrm{4}}{t}^{\mathrm{2}} −\frac{\mathrm{57}}{\mathrm{2}}{t}−\frac{\mathrm{63}}{\mathrm{4}}=\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{this}\:\mathrm{has}\:\mathrm{no}\:“\mathrm{nice}''\:\mathrm{solution} \\ $$
Commented by MathsFan last updated on 08/Nov/21

$$\mathrm{okay}\:\mathrm{sir} \\ $$$$\mathrm{thanks} \\ $$
