Question Number 158697 by amin96 last updated on 07/Nov/21
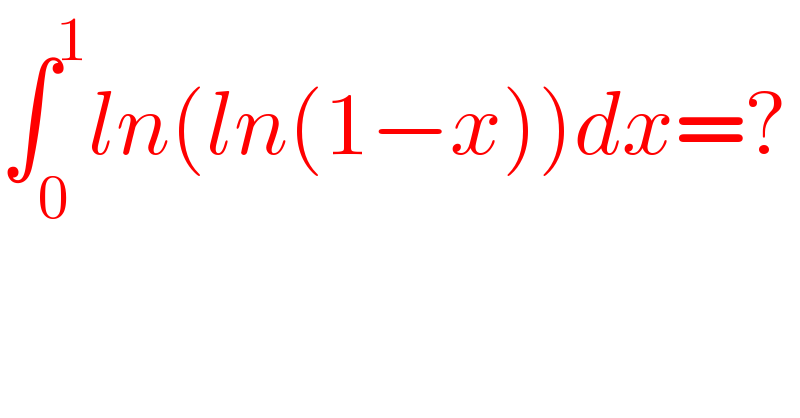
$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({ln}\left(\mathrm{1}−{x}\right)\right){dx}=? \\ $$
Answered by mnjuly1970 last updated on 08/Nov/21
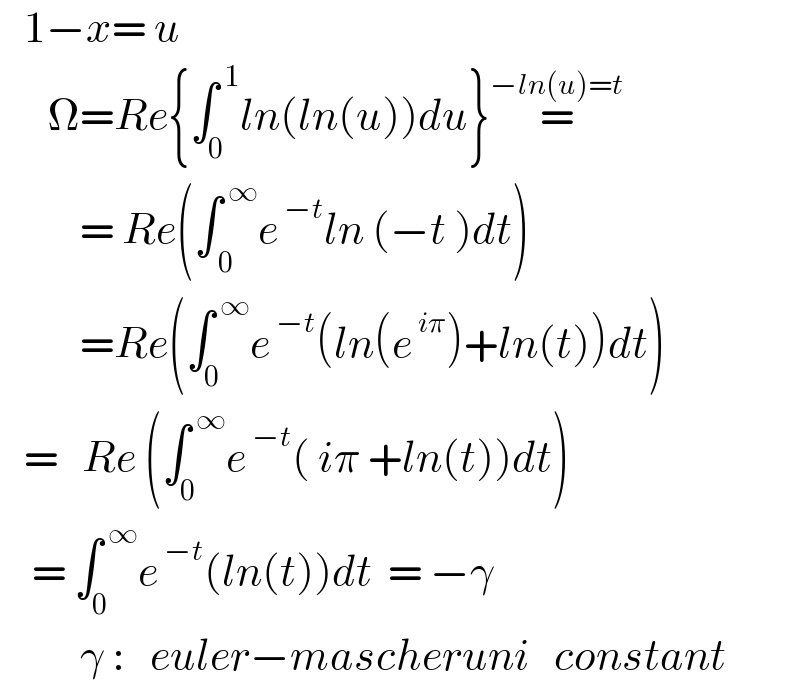
$$\:\:\:\mathrm{1}−{x}=\:{u}\: \\ $$$$\:\:\:\:\:\:\Omega={Re}\left\{\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left({ln}\left({u}\right)\right){du}\right\}\overset{−{ln}\left({u}\right)={t}} {=} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:{Re}\left(\int_{\:\mathrm{0}} ^{\:\infty} {e}^{\:−{t}} {ln}\:\left(−{t}\:\right){dt}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:={Re}\left(\int_{\mathrm{0}} ^{\:\infty} {e}^{\:−{t}} \left({ln}\left({e}^{\:{i}\pi} \right)+{ln}\left({t}\right)\right){dt}\right) \\ $$$$\:\:\:=\:\:\:{Re}\:\left(\int_{\mathrm{0}} ^{\:\infty} {e}^{\:−{t}} \left(\:{i}\pi\:+{ln}\left({t}\right)\right){dt}\right) \\ $$$$\:\:\:\:=\:\int_{\mathrm{0}} ^{\:\infty} {e}^{\:−{t}} \left({ln}\left({t}\right)\right){dt}\:\:=\:−\gamma \\ $$$$\:\:\:\:\:\:\:\:\:\:\gamma\::\:\:\:{euler}−{mascheruni}\:\:\:{constant} \\ $$
