A-positive-number-has-8-distinct-divisors-Lets-say-a-b-c-d-e-f-g-and-h-Given-a-b-c-d-e-f-g-h-3111696-Find-that-number-

Question Number 27651 by Joel578 last updated on 12/Jan/18

$$\mathrm{A}\:\mathrm{positive}\:\mathrm{number}\:\mathrm{has}\:\mathrm{8}\:\mathrm{distinct}\:\mathrm{divisors} \\ $$$$\mathrm{Lets}\:\mathrm{say}\:{a},\:{b},\:{c},\:{d},\:{e},\:{f},\:{g}\:\mathrm{and}\:{h} \\ $$$$\mathrm{Given}\:\:{a}\:.\:{b}\:.\:{c}\:.\:{d}\:.\:{e}\:.\:{f}\:.\:{g}\:.\:{h}\:=\:\mathrm{3111696} \\ $$$$\mathrm{Find}\:\mathrm{that}\:\mathrm{number} \\ $$

Commented by Joel578 last updated on 12/Jan/18

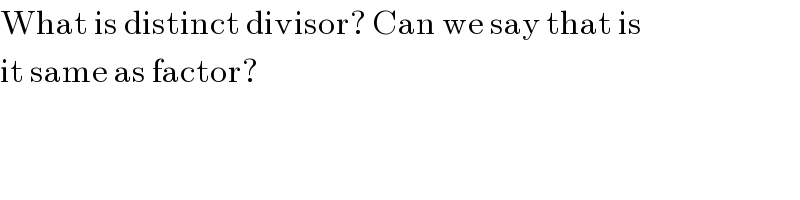
What is distinct divisor? Can we say that is it same as factor?

$$\mathrm{What}\:\mathrm{is}\:\mathrm{distinct}\:\mathrm{divisor}?\:\mathrm{Can}\:\mathrm{we}\:\mathrm{say}\:\mathrm{that}\:\mathrm{is} \\ $$$$\mathrm{it}\:\mathrm{same}\:\mathrm{as}\:\mathrm{factor}? \\ $$

Commented by Rasheed.Sindhi last updated on 14/Jan/18

Distinct divisors means differnt divisors and yes divisor is same as factor. If a∣c & b∣c & a≠b then a and b are distinct divisors.

$$\mathrm{Distinct}\:\mathrm{divisors}\:\mathrm{means}\:\mathrm{differnt} \\ $$$$\mathrm{divisors}\:\mathrm{and}\:\mathrm{yes}\:\mathrm{divisor}\:\mathrm{is}\:\mathrm{same} \\ $$$$\mathrm{as}\:\mathrm{factor}. \\ $$$$\mathrm{If}\:\:\mathrm{a}\mid\mathrm{c}\:\&\:\mathrm{b}\mid\mathrm{c}\:\&\:\mathrm{a}\neq\mathrm{b}\:\mathrm{then}\:\mathrm{a}\:\mathrm{and}\:\mathrm{b} \\ $$$$\mathrm{are}\:\boldsymbol{\mathrm{distinct}}\:\boldsymbol{\mathrm{divisors}}. \\ $$$$ \\ $$

Answered by mrW2 last updated on 14/Jan/18

The number is 2×3×7=42. It has exactly 8 (distinct) divisors: 1 (=a) 2 (=b) 3 (=c) 6 (=d) 7 (=e) 14 (=f) 21 (=g) 42 (=h) The product of all those divisors is a∙b∙c∙d∙e∙f∙g∙h=1×2×3×6×7×14×21×42=311696

$${The}\:{number}\:{is}\:\mathrm{2}×\mathrm{3}×\mathrm{7}=\mathrm{42}.\:{It}\:{has} \\ $$$${exactly}\:\mathrm{8}\:\left({distinct}\right)\:{divisors}: \\ $$$$\mathrm{1}\:\left(={a}\right) \\ $$$$\mathrm{2}\:\left(={b}\right) \\ $$$$\mathrm{3}\:\left(={c}\right) \\ $$$$\mathrm{6}\:\left(={d}\right) \\ $$$$\mathrm{7}\:\left(={e}\right) \\ $$$$\mathrm{14}\:\left(={f}\right) \\ $$$$\mathrm{21}\:\left(={g}\right) \\ $$$$\mathrm{42}\:\left(={h}\right) \\ $$$${The}\:{product}\:{of}\:{all}\:{those}\:{divisors}\:{is} \\ $$$${a}\centerdot{b}\centerdot{c}\centerdot{d}\centerdot{e}\centerdot{f}\centerdot{g}\centerdot{h}=\mathrm{1}×\mathrm{2}×\mathrm{3}×\mathrm{6}×\mathrm{7}×\mathrm{14}×\mathrm{21}×\mathrm{42}=\mathrm{311696} \\ $$

Commented by Rasheed.Sindhi last updated on 13/Jan/18

Hi Sir mrW1∣ mrW2 Your answer is perfect as it contains all the divisors of required number. I deleted my answer because its logic was deffective.

$$\mathrm{Hi}\:\mathrm{Sir}\:\mathrm{mrW1}\mid\:\mathrm{mrW2} \\ $$$$\mathrm{Your}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{perfect}\:\mathrm{as}\:\mathrm{it}\:\mathrm{contains} \\ $$$$\mathrm{all}\:\mathrm{the}\:\mathrm{divisors}\:\mathrm{of}\:\mathrm{required}\:\mathrm{number}. \\ $$$$\mathrm{I}\:\mathrm{deleted}\:\mathrm{my}\:\mathrm{answer}\:\mathrm{because}\:\mathrm{its} \\ $$$$\mathrm{logic}\:\mathrm{was}\:\mathrm{deffective}. \\ $$

Commented by mrW2 last updated on 13/Jan/18

$${Sir},\:{to}\:{be}\:{honest},\:{I}\:{didn}'{t}\:{catch}\:{the} \\ $$$${question}\:{really}\:{till}\:{I}\:{saw}\:{your}\:{working}. \\ $$$${It}\:{brought}\:{me}\:{finally}\:{to}\:{the}\:{right}\: \\ $$$${understanding}\:{and}\:{to}\:{the}\:{answer}.\: \\ $$$${Therefore}\:{thank}\:{you}\:{for}\:{your}\:{working}! \\ $$

Commented by Rasheed.Sindhi last updated on 13/Jan/18

ThAnKs SiR! Could You Help Me in solving Q#27422 & Q27627.

$$\mathbb{T}{h}\mathbb{A}{n}\mathbb{K}{s}\:\mathbb{S}{i}\mathbb{R}!\: \\ $$$$\:\:\:\mathbb{C}\mathrm{ould}\:\mathbb{Y}\mathrm{ou}\:\mathbb{H}\mathrm{elp}\:\mathbb{M}\mathrm{e}\:\mathrm{in}\:\mathrm{solving} \\ $$$$\mathbb{Q}#\mathrm{27422}\:\&\:\mathbb{Q}\mathrm{27627}. \\ $$$$ \\ $$

Answered by mrW2 last updated on 14/Jan/18

An other way to solve this question: We know the number, let′s say N has 8 different divisors a, b, c..., h. We know if number k is a divisor of N, then (N/k) must be an other divisor of it, the product of both divisors is N. This is to say if we arrange a, b,c...,h increasingly, we′ll have a∙h=N b∙g=N c∙f=N d∙e=N Then we′ll get a∙b∙c∙d∙e∙f∙g∙h=N^4 =3111696 (as given) according to Sir Rasheed.Sindhi: 3111696=(2×3×7)^4 ⇒N=2×3×7=42

$${An}\:{other}\:{way}\:{to}\:{solve}\:{this}\:{question}: \\ $$$${We}\:{know}\:{the}\:{number},\:{let}'{s}\:{say}\:{N}\:{has} \\ $$$$\mathrm{8}\:{different}\:{divisors}\:{a},\:{b},\:{c}…,\:{h}. \\ $$$$ \\ $$$${We}\:{know}\:{if}\:{number}\:{k}\:{is}\:{a}\:{divisor}\:{of} \\ $$$${N},\:{then}\:\frac{{N}}{{k}}\:{must}\:{be}\:{an}\:{other}\:{divisor}\:{of} \\ $$$${it},\:{the}\:{product}\:{of}\:{both}\:{divisors}\:{is}\:{N}. \\ $$$$ \\ $$$${This}\:{is}\:{to}\:{say}\:{if}\:{we}\:{arrange}\:{a},\:{b},{c}…,{h} \\ $$$${increasingly},\:{we}'{ll}\:{have} \\ $$$${a}\centerdot{h}={N} \\ $$$${b}\centerdot{g}={N} \\ $$$${c}\centerdot{f}={N} \\ $$$${d}\centerdot{e}={N} \\ $$$${Then}\:{we}'{ll}\:{get}\: \\ $$$${a}\centerdot{b}\centerdot{c}\centerdot{d}\centerdot{e}\centerdot{f}\centerdot{g}\centerdot{h}={N}^{\mathrm{4}} =\mathrm{3111696}\:\left({as}\:{given}\right) \\ $$$${according}\:{to}\:{Sir}\:{Rasheed}.{Sindhi}:\:\mathrm{3111696}=\left(\mathrm{2}×\mathrm{3}×\mathrm{7}\right)^{\mathrm{4}} \\ $$$$\Rightarrow{N}=\mathrm{2}×\mathrm{3}×\mathrm{7}=\mathrm{42} \\ $$

Commented by Rasheed.Sindhi last updated on 14/Jan/18

Creative work Sir! This is realy a ′ method ′for such problems!

$$\boldsymbol{{Creative}}\:\boldsymbol{{work}}\:\boldsymbol{{Sir}}! \\ $$$$\:{This}\:{is}\:{realy}\:{a}\:'\:\boldsymbol{{method}}\:'{for}\: \\ $$$${such}\:{problems}!\: \\ $$

Commented by Joel578 last updated on 14/Jan/18

$${thank}\:{you}\:{very}\:{much} \\ $$

Facebook Tweet Pin

A-positive-number-has-8-distinct-divisors-Lets-say-a-b-c-d-e-f-g-and-h-Given-a-b-c-d-e-f-g-h-3111696-Find-that-number-

Leave a Reply Cancel reply