Menu Close

Question-158749

Tinku Tara 0 Comments
Pin




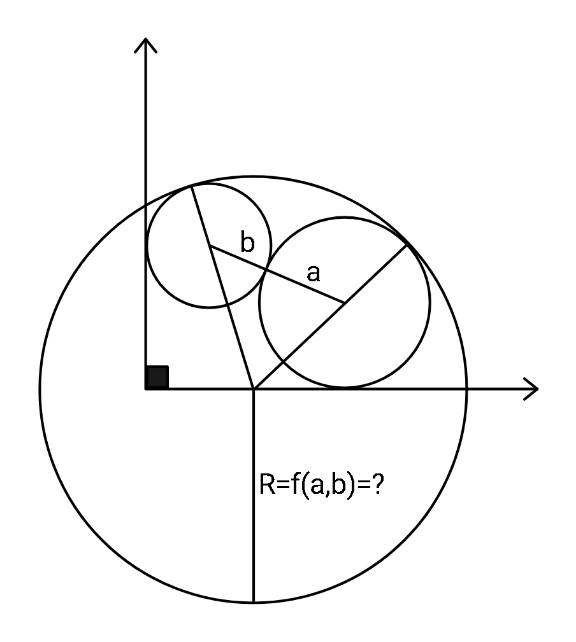
Question Number 158749 by ajfour last updated on 08/Nov/21
Commented by ajfour last updated on 08/Nov/21
Find extreme values of R.
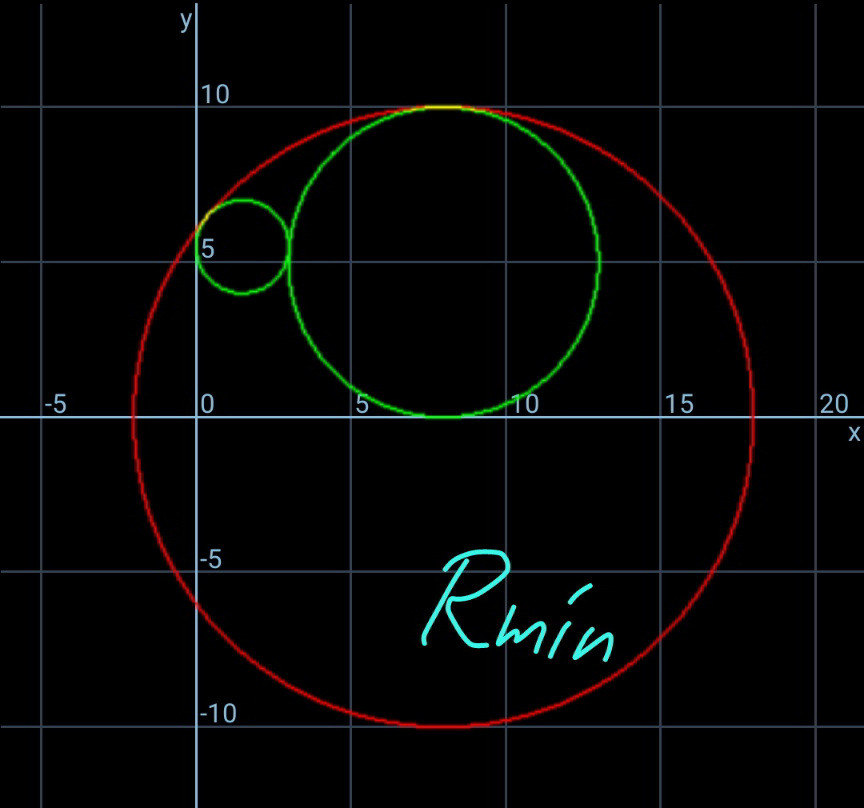
$${Find}\:{extreme}\:{values}\:{of}\:{R}. \\ $$
Answered by mr W last updated on 08/Nov/21
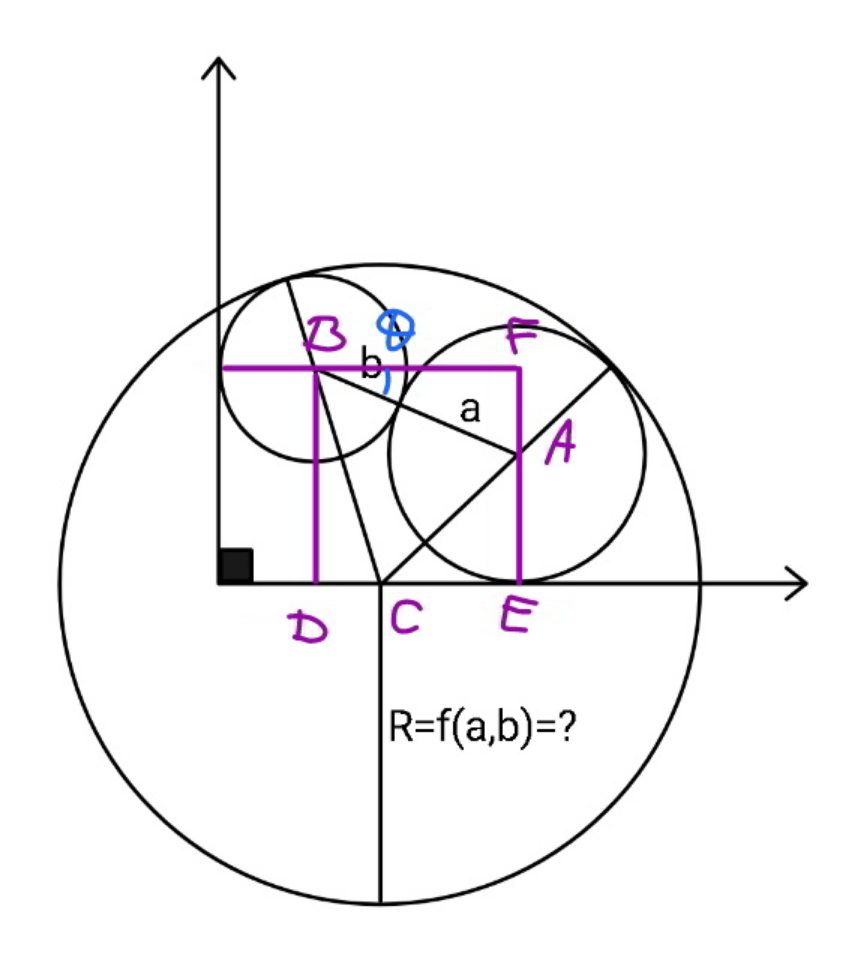
Commented by mr W last updated on 08/Nov/21
let c=a+b let μ=(b/a), λ=(R/a) BD=a+c sin θ DC=(√((R−b)^2 −(a+c sin θ)^2 )) CE=(√((R−a)^2 −a^2 ))=(√(R^2 −2aR)) DE=BF=c cos θ c cos θ=(√((R−b)^2 −(a+c sin θ)^2 ))+(√(R^2 −2aR)) c cos θ−(√(R^2 −2aR))=(√((R−b)^2 −(a+c sin θ)^2 )) c^2 cos^2 θ−2c cos θ(√(R^2 −2aR))=2(a−b)R+b^2 −(a+c sin θ)^2 a(1+sin θ)−((a−b)/(a+b))R=cos θ(√(R^2 −2aR)) (1+sin θ)−((1−μ)/(1+μ))λ=cos θ(√(λ^2 −2λ)) (((1−μ)/(1+μ)))^2 λ^2 +(1+sin θ)^2 −2(((1−μ)/(1+μ)))(1+sin θ)λ=cos^2 θλ^2 −2cos^2 θλ [(((1−μ)/(1+μ)))^2 −cos^2 θ]λ^2 −2[(1+sin θ)(((1−μ)/(1+μ)))−cos^2 θ]λ+(1+sin θ)^2 =0 [(((1−μ)/(1+μ)))^2 −cos^2 θ]λ^2 −2(1+sin θ)(sin θ−((2μ)/(1+μ)))λ+(1+sin θ)^2 =0 λ=(((1+sin θ)(sin θ−((2μ)/(1+μ)))−(1+sin θ)(√((sin θ−((2μ)/(1+μ)))^2 −(((1−μ)/(1+μ)))^2 +cos^2 θ)))/((((1−μ)/(1+μ)))^2 −cos^2 θ)) λ=(((1+sin θ){sin θ−((2μ)/(1+μ))−(√((4μ(1−sin θ))/(1+μ)))})/((((1−μ)/(1+μ)))^2 −cos^2 θ)) or λ=(((1+sin θ)[ξ+(√(2ξ(1−sin θ)))−sin θ])/(ξ(2−ξ)−sin^2 θ)) with ξ=((2μ)/(1+μ))=((2b)/(a+b))
$${let}\:{c}={a}+{b} \\ $$$${let}\:\mu=\frac{{b}}{{a}},\:\lambda=\frac{{R}}{{a}} \\ $$$${BD}={a}+{c}\:\mathrm{sin}\:\theta \\ $$$${DC}=\sqrt{\left({R}−{b}\right)^{\mathrm{2}} −\left({a}+{c}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} } \\ $$$${CE}=\sqrt{\left({R}−{a}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} }=\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{aR}} \\ $$$${DE}={BF}={c}\:\mathrm{cos}\:\theta \\ $$$${c}\:\mathrm{cos}\:\theta=\sqrt{\left({R}−{b}\right)^{\mathrm{2}} −\left({a}+{c}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} }+\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{aR}} \\ $$$${c}\:\mathrm{cos}\:\theta−\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{aR}}=\sqrt{\left({R}−{b}\right)^{\mathrm{2}} −\left({a}+{c}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} } \\ $$$${c}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{2}{c}\:\mathrm{cos}\:\theta\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{aR}}=\mathrm{2}\left({a}−{b}\right){R}+{b}^{\mathrm{2}} −\left({a}+{c}\:\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$${a}\left(\mathrm{1}+\mathrm{sin}\:\theta\right)−\frac{{a}−{b}}{{a}+{b}}{R}=\mathrm{cos}\:\theta\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{aR}} \\ $$$$\left(\mathrm{1}+\mathrm{sin}\:\theta\right)−\frac{\mathrm{1}−\mu}{\mathrm{1}+\mu}\lambda=\mathrm{cos}\:\theta\sqrt{\lambda^{\mathrm{2}} −\mathrm{2}\lambda} \\ $$$$\left(\frac{\mathrm{1}−\mu}{\mathrm{1}+\mu}\right)^{\mathrm{2}} \lambda^{\mathrm{2}} +\left(\mathrm{1}+\mathrm{sin}\:\theta\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{\mathrm{1}−\mu}{\mathrm{1}+\mu}\right)\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\lambda=\mathrm{cos}^{\mathrm{2}} \:\theta\lambda^{\mathrm{2}} −\mathrm{2cos}^{\mathrm{2}} \:\theta\lambda \\ $$$$\left[\left(\frac{\mathrm{1}−\mu}{\mathrm{1}+\mu}\right)^{\mathrm{2}} −\mathrm{cos}^{\mathrm{2}} \:\theta\right]\lambda^{\mathrm{2}} −\mathrm{2}\left[\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\left(\frac{\mathrm{1}−\mu}{\mathrm{1}+\mu}\right)−\mathrm{cos}^{\mathrm{2}} \:\theta\right]\lambda+\left(\mathrm{1}+\mathrm{sin}\:\theta\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\left[\left(\frac{\mathrm{1}−\mu}{\mathrm{1}+\mu}\right)^{\mathrm{2}} −\mathrm{cos}^{\mathrm{2}} \:\theta\right]\lambda^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\left(\mathrm{sin}\:\theta−\frac{\mathrm{2}\mu}{\mathrm{1}+\mu}\right)\lambda+\left(\mathrm{1}+\mathrm{sin}\:\theta\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\lambda=\frac{\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\left(\mathrm{sin}\:\theta−\frac{\mathrm{2}\mu}{\mathrm{1}+\mu}\right)−\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\sqrt{\left(\mathrm{sin}\:\theta−\frac{\mathrm{2}\mu}{\mathrm{1}+\mu}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}−\mu}{\mathrm{1}+\mu}\right)^{\mathrm{2}} +\mathrm{cos}^{\mathrm{2}} \:\theta}}{\left(\frac{\mathrm{1}−\mu}{\mathrm{1}+\mu}\right)^{\mathrm{2}} −\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\lambda=\frac{\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\left\{\mathrm{sin}\:\theta−\frac{\mathrm{2}\mu}{\mathrm{1}+\mu}−\sqrt{\frac{\mathrm{4}\mu\left(\mathrm{1}−\mathrm{sin}\:\theta\right)}{\mathrm{1}+\mu}}\right\}}{\left(\frac{\mathrm{1}−\mu}{\mathrm{1}+\mu}\right)^{\mathrm{2}} −\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$${or} \\ $$$$\lambda=\frac{\left(\mathrm{1}+\mathrm{sin}\:\theta\right)\left[\xi+\sqrt{\mathrm{2}\xi\left(\mathrm{1}−\mathrm{sin}\:\theta\right)}−\mathrm{sin}\:\theta\right]}{\xi\left(\mathrm{2}−\xi\right)−\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$${with}\:\xi=\frac{\mathrm{2}\mu}{\mathrm{1}+\mu}=\frac{\mathrm{2}{b}}{{a}+{b}} \\ $$
Commented by ajfour last updated on 08/Nov/21
Thank you Sir Seems satisfactory!
$$\:\:\:\:\:\:\:\:\:\:\:{Thank}\:{you}\:{Sir}\: \\ $$$$\:\:\:\:{Seems}\:{satisfactory}! \\ $$
Commented by mr W last updated on 08/Nov/21
Commented by mr W last updated on 08/Nov/21
Commented by mr W last updated on 08/Nov/21
Commented by mr W last updated on 08/Nov/21
Commented by mr W last updated on 08/Nov/21
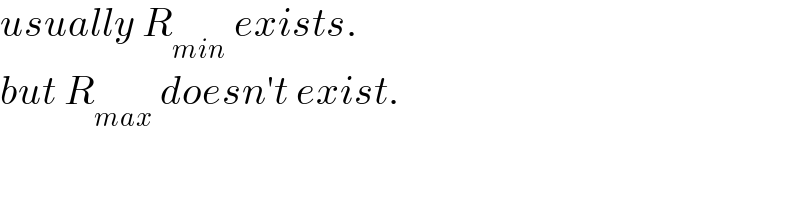
usually R_(min) exists. but R_(max) doesn′t exist.
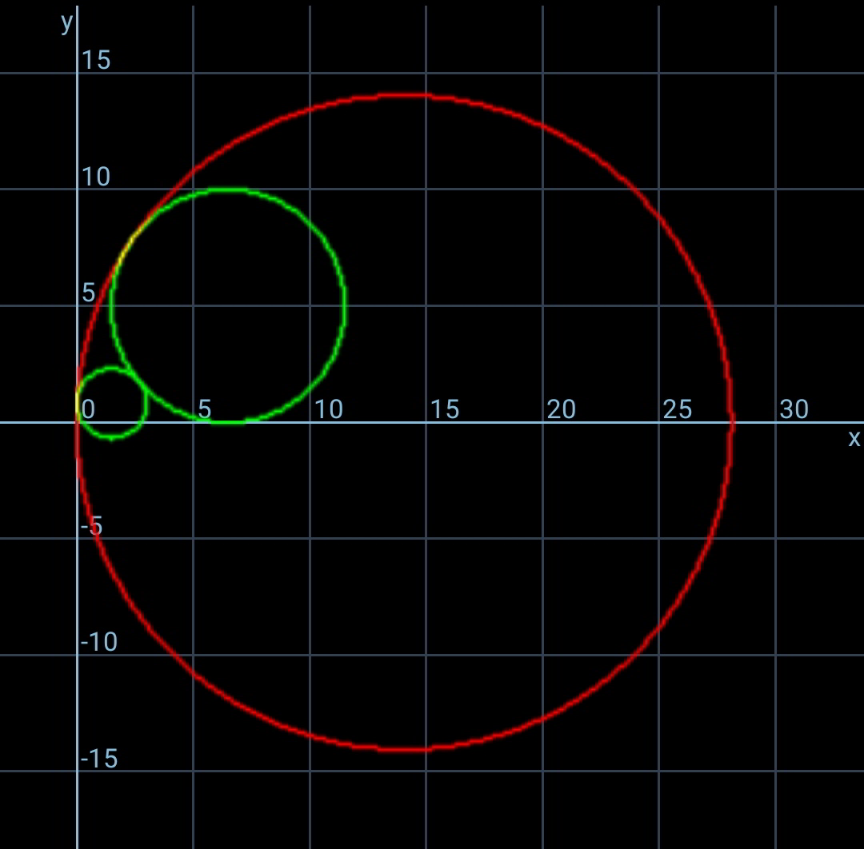
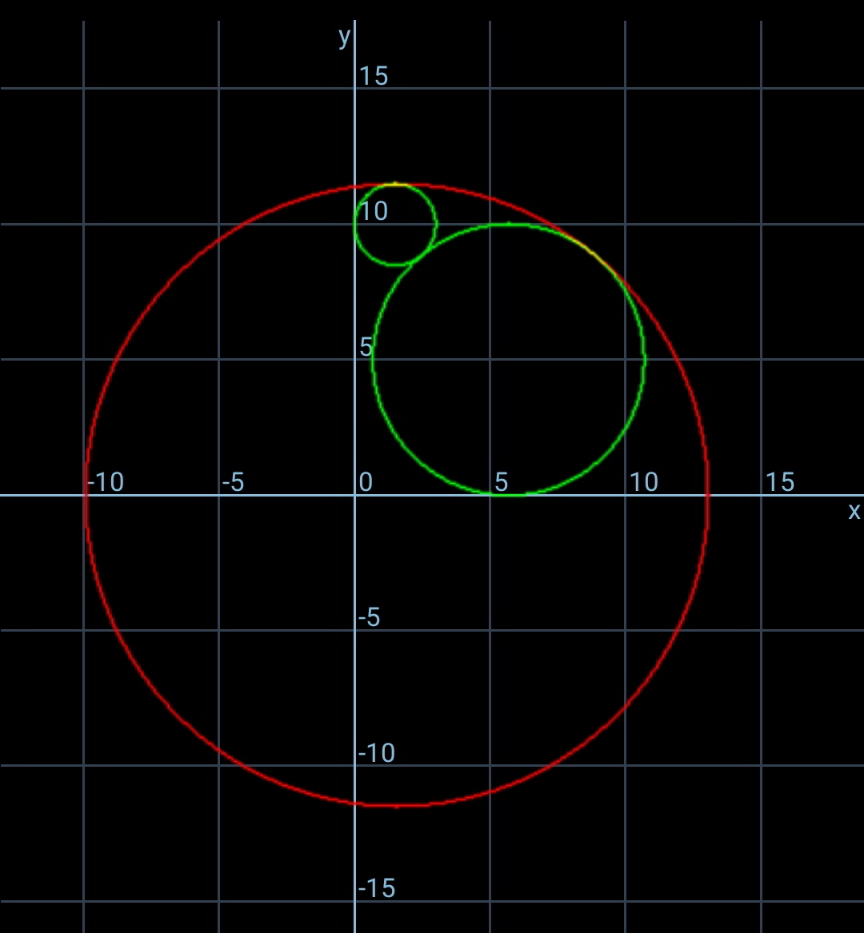
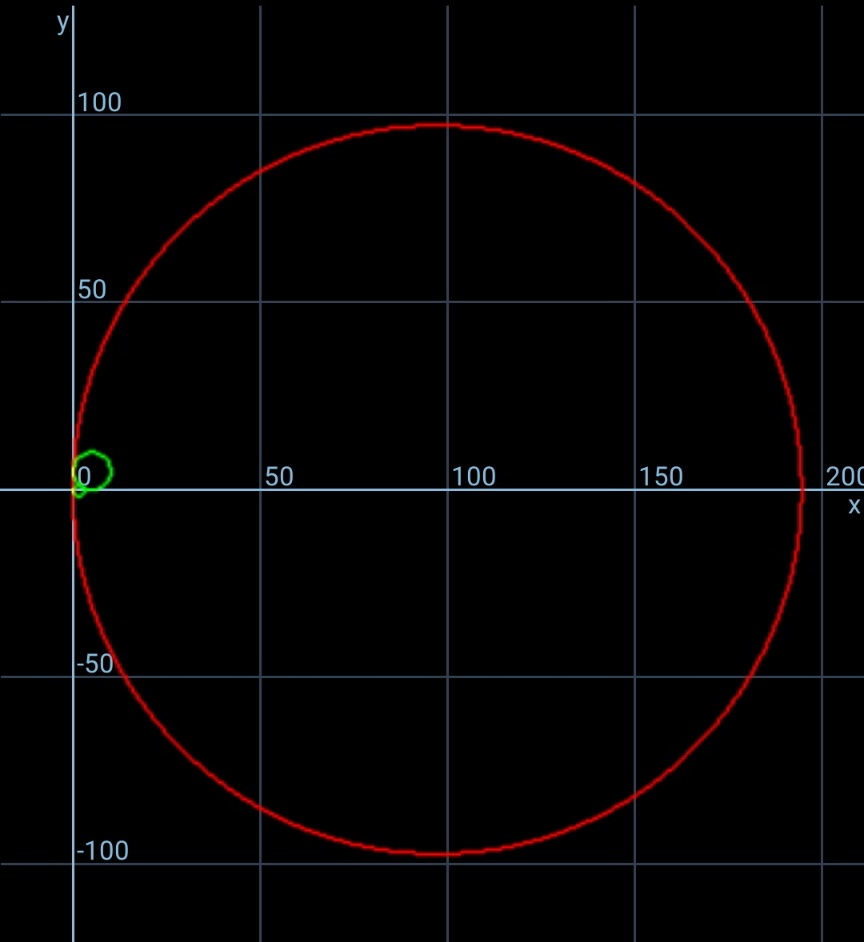
$${usually}\:{R}_{{min}} \:{exists}. \\ $$$${but}\:{R}_{{max}} \:{doesn}'{t}\:{exist}. \\ $$
Commented by mr W last updated on 09/Nov/21
Commented by ajfour last updated on 09/Nov/21
The situation is: a≥b. A is in contact with ground and B. B in contact with wall and A;(just the 1^(st) quadrant).
$${The}\:{situation}\:{is}:\:\:{a}\geqslant{b}.\:{A}\:{is} \\ $$$${in}\:{contact}\:{with}\:{ground}\:{and} \\ $$$${B}.\:{B}\:{in}\:{contact}\:{with}\:{wall} \\ $$$${and}\:{A};\left({just}\:{the}\:\mathrm{1}^{{st}} \:{quadrant}\right). \\ $$
Commented by mr W last updated on 09/Nov/21
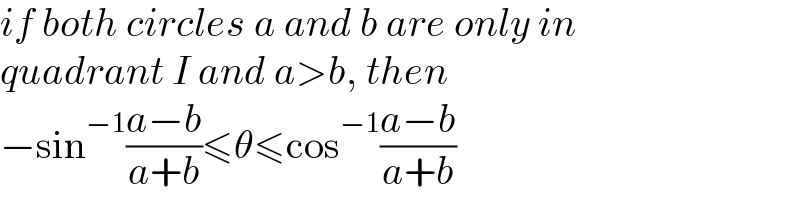
if both circles a and b are only in quadrant I and a>b, then −sin^(−1) ((a−b)/(a+b))≤θ≤cos^(−1) ((a−b)/(a+b))
$${if}\:{both}\:{circles}\:{a}\:{and}\:{b}\:{are}\:{only}\:{in} \\ $$$${quadrant}\:{I}\:{and}\:{a}>{b},\:{then} \\ $$$$−\mathrm{sin}^{−\mathrm{1}} \frac{{a}−{b}}{{a}+{b}}\leqslant\theta\leqslant\mathrm{cos}^{−\mathrm{1}} \frac{{a}−{b}}{{a}+{b}} \\ $$
Commented by mr W last updated on 09/Nov/21
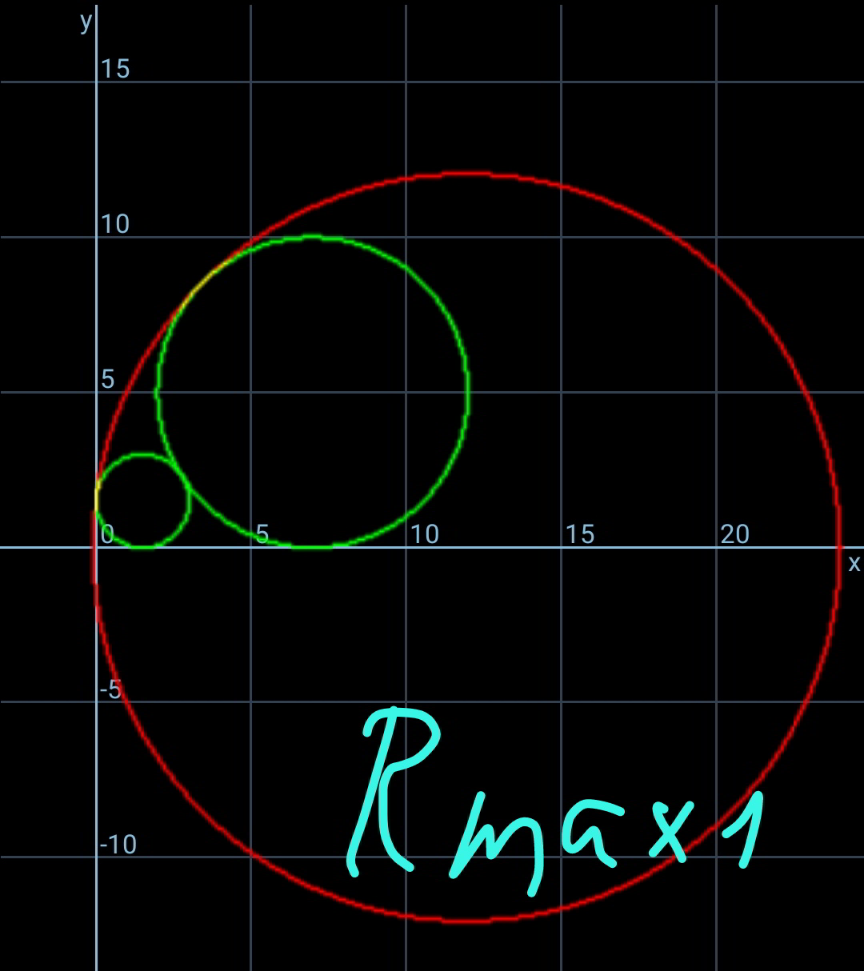
Commented by Tawa11 last updated on 16/Nov/21
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by ajfour last updated on 08/Nov/21
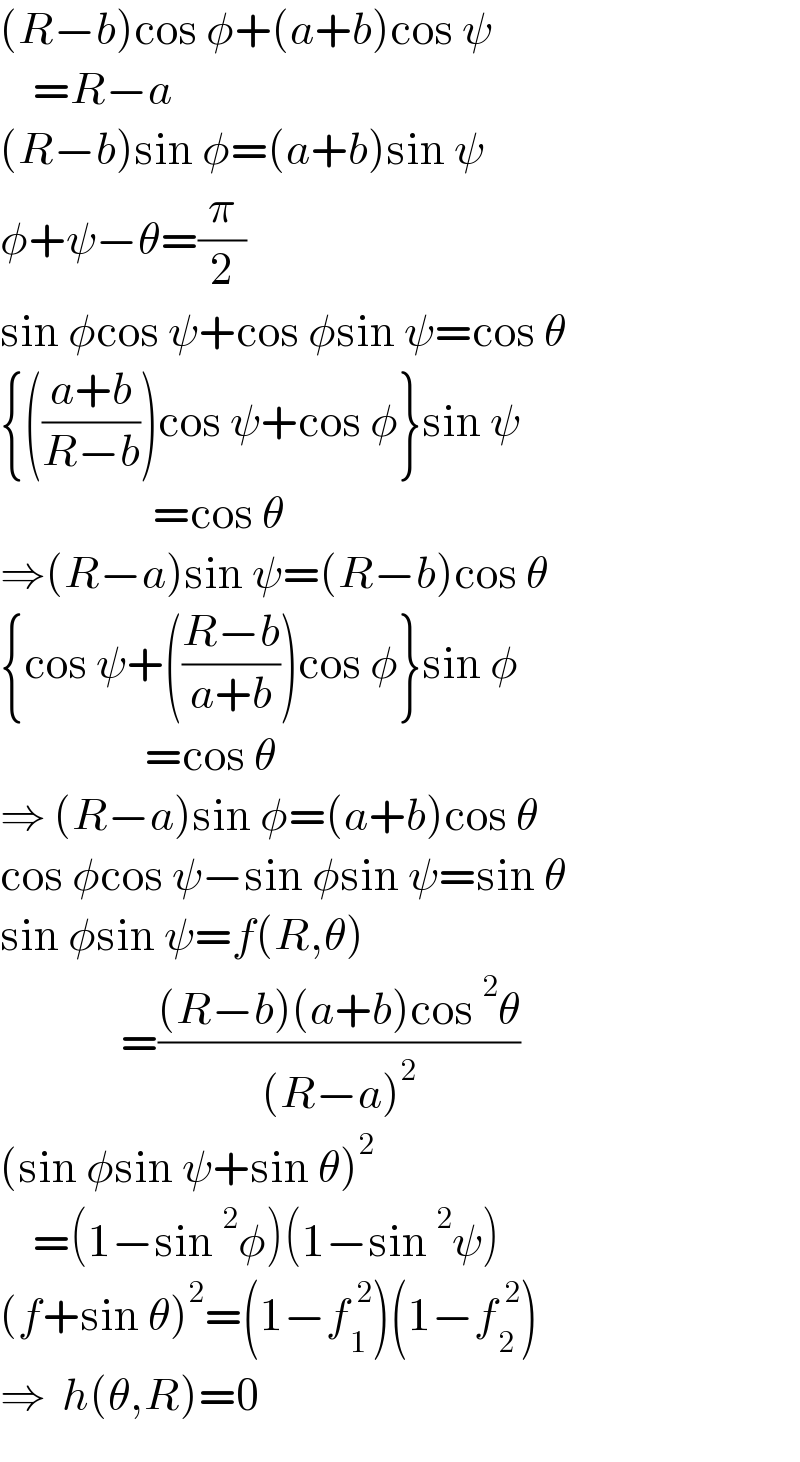
(R−b)cos φ+(a+b)cos ψ =R−a (R−b)sin φ=(a+b)sin ψ φ+ψ−θ=(π/2) sin φcos ψ+cos φsin ψ=cos θ {(((a+b)/(R−b)))cos ψ+cos φ}sin ψ =cos θ ⇒(R−a)sin ψ=(R−b)cos θ {cos ψ+(((R−b)/(a+b)))cos φ}sin φ =cos θ ⇒ (R−a)sin φ=(a+b)cos θ cos φcos ψ−sin φsin ψ=sin θ sin φsin ψ=f(R,θ) =(((R−b)(a+b)cos^2 θ)/((R−a)^2 )) (sin φsin ψ+sin θ)^2 =(1−sin^2 φ)(1−sin^2 ψ) (f+sin θ)^2 =(1−f_1 ^( 2) )(1−f_2 ^( 2) ) ⇒ h(θ,R)=0
$$\left({R}−{b}\right)\mathrm{cos}\:\phi+\left({a}+{b}\right)\mathrm{cos}\:\psi \\ $$$$\:\:\:\:={R}−{a} \\ $$$$\left({R}−{b}\right)\mathrm{sin}\:\phi=\left({a}+{b}\right)\mathrm{sin}\:\psi \\ $$$$\phi+\psi−\theta=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\phi\mathrm{cos}\:\psi+\mathrm{cos}\:\phi\mathrm{sin}\:\psi=\mathrm{cos}\:\theta \\ $$$$\left\{\left(\frac{{a}+{b}}{{R}−{b}}\right)\mathrm{cos}\:\psi+\mathrm{cos}\:\phi\right\}\mathrm{sin}\:\psi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{cos}\:\theta \\ $$$$\Rightarrow\left({R}−{a}\right)\mathrm{sin}\:\psi=\left({R}−{b}\right)\mathrm{cos}\:\theta \\ $$$$\left\{\mathrm{cos}\:\psi+\left(\frac{{R}−{b}}{{a}+{b}}\right)\mathrm{cos}\:\phi\right\}\mathrm{sin}\:\phi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{cos}\:\theta \\ $$$$\Rightarrow\:\left({R}−{a}\right)\mathrm{sin}\:\phi=\left({a}+{b}\right)\mathrm{cos}\:\theta \\ $$$$\mathrm{cos}\:\phi\mathrm{cos}\:\psi−\mathrm{sin}\:\phi\mathrm{sin}\:\psi=\mathrm{sin}\:\theta \\ $$$$\mathrm{sin}\:\phi\mathrm{sin}\:\psi={f}\left({R},\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left({R}−{b}\right)\left({a}+{b}\right)\mathrm{cos}\:^{\mathrm{2}} \theta}{\left({R}−{a}\right)^{\mathrm{2}} } \\ $$$$\left(\mathrm{sin}\:\phi\mathrm{sin}\:\psi+\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$$\:\:\:\:=\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \phi\right)\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \psi\right) \\ $$$$\left({f}+\mathrm{sin}\:\theta\right)^{\mathrm{2}} =\left(\mathrm{1}−{f}_{\mathrm{1}} ^{\:\mathrm{2}} \right)\left(\mathrm{1}−{f}_{\mathrm{2}} ^{\:\mathrm{2}} \right) \\ $$$$\Rightarrow\:\:{h}\left(\theta,{R}\right)=\mathrm{0} \\ $$
Commented by ajfour last updated on 08/Nov/21
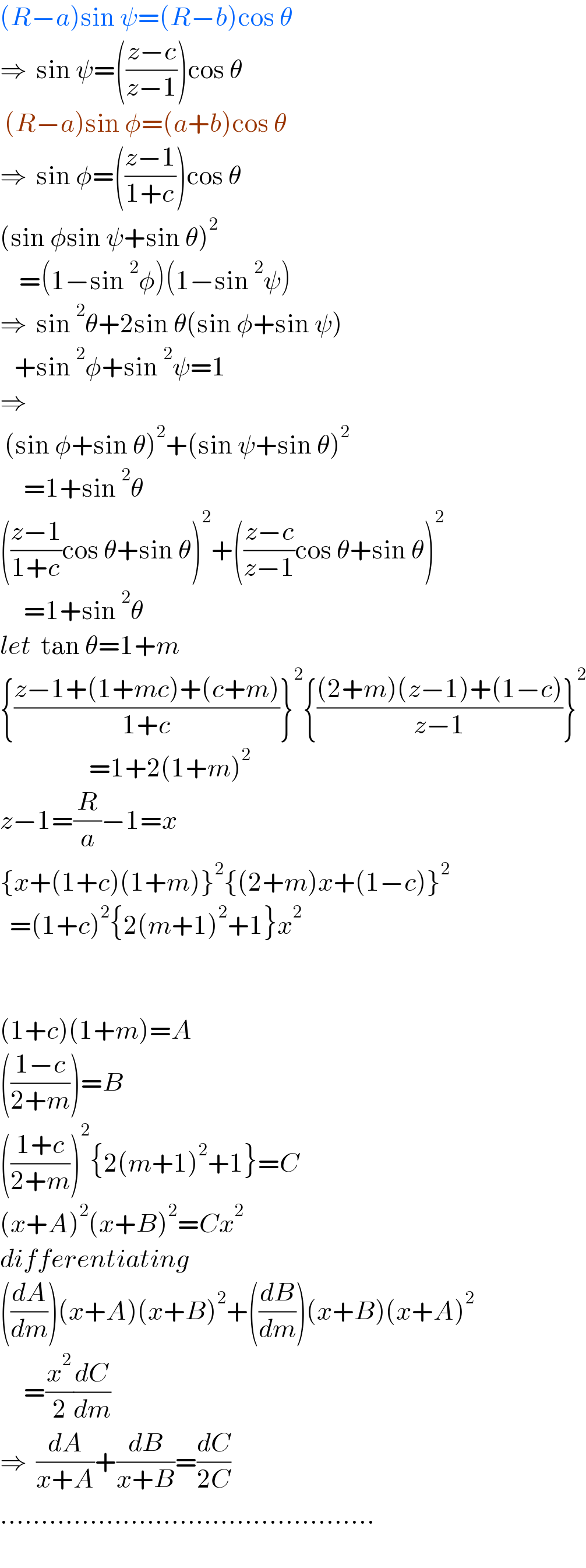
(R−a)sin ψ=(R−b)cos θ ⇒ sin ψ=(((z−c)/(z−1)))cos θ (R−a)sin φ=(a+b)cos θ ⇒ sin φ=(((z−1)/(1+c)))cos θ (sin φsin ψ+sin θ)^2 =(1−sin^2 φ)(1−sin^2 ψ) ⇒ sin^2 θ+2sin θ(sin φ+sin ψ) +sin^2 φ+sin^2 ψ=1 ⇒ (sin φ+sin θ)^2 +(sin ψ+sin θ)^2 =1+sin^2 θ (((z−1)/(1+c))cos θ+sin θ)^2 +(((z−c)/(z−1))cos θ+sin θ)^2 =1+sin^2 θ let tan θ=1+m {((z−1+(1+mc)+(c+m))/(1+c))}^2 {(((2+m)(z−1)+(1−c))/(z−1))}^2 =1+2(1+m)^2 z−1=(R/a)−1=x {x+(1+c)(1+m)}^2 {(2+m)x+(1−c)}^2 =(1+c)^2 {2(m+1)^2 +1}x^2 (1+c)(1+m)=A (((1−c)/(2+m)))=B (((1+c)/(2+m)))^2 {2(m+1)^2 +1}=C (x+A)^2 (x+B)^2 =Cx^2 differentiating ((dA/dm))(x+A)(x+B)^2 +((dB/dm))(x+B)(x+A)^2 =(x^2 /2)(dC/dm) ⇒ (dA/(x+A))+(dB/(x+B))=(dC/(2C)) ..............................................
$$\left({R}−{a}\right)\mathrm{sin}\:\psi=\left({R}−{b}\right)\mathrm{cos}\:\theta \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\psi=\left(\frac{{z}−{c}}{{z}−\mathrm{1}}\right)\mathrm{cos}\:\theta \\ $$$$\:\left({R}−{a}\right)\mathrm{sin}\:\phi=\left({a}+{b}\right)\mathrm{cos}\:\theta \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\phi=\left(\frac{{z}−\mathrm{1}}{\mathrm{1}+{c}}\right)\mathrm{cos}\:\theta \\ $$$$\left(\mathrm{sin}\:\phi\mathrm{sin}\:\psi+\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$$\:\:\:\:=\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \phi\right)\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \psi\right) \\ $$$$\Rightarrow\:\:\mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{2sin}\:\theta\left(\mathrm{sin}\:\phi+\mathrm{sin}\:\psi\right) \\ $$$$\:\:\:+\mathrm{sin}\:^{\mathrm{2}} \phi+\mathrm{sin}\:^{\mathrm{2}} \psi=\mathrm{1}\:\: \\ $$$$\Rightarrow \\ $$$$\:\left(\mathrm{sin}\:\phi+\mathrm{sin}\:\theta\right)^{\mathrm{2}} +\left(\mathrm{sin}\:\psi+\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:=\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \theta \\ $$$$\left(\frac{{z}−\mathrm{1}}{\mathrm{1}+{c}}\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right)^{\mathrm{2}} +\left(\frac{{z}−{c}}{{z}−\mathrm{1}}\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:=\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \theta \\ $$$${let}\:\:\mathrm{tan}\:\theta=\mathrm{1}+{m} \\ $$$$\left\{\frac{{z}−\mathrm{1}+\left(\mathrm{1}+{mc}\right)+\left({c}+{m}\right)}{\mathrm{1}+{c}}\right\}^{\mathrm{2}} \left\{\frac{\left(\mathrm{2}+{m}\right)\left({z}−\mathrm{1}\right)+\left(\mathrm{1}−{c}\right)}{{z}−\mathrm{1}}\right\}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}+\mathrm{2}\left(\mathrm{1}+{m}\right)^{\mathrm{2}} \\ $$$${z}−\mathrm{1}=\frac{{R}}{{a}}−\mathrm{1}={x} \\ $$$$\left\{{x}+\left(\mathrm{1}+{c}\right)\left(\mathrm{1}+{m}\right)\right\}^{\mathrm{2}} \left\{\left(\mathrm{2}+{m}\right){x}+\left(\mathrm{1}−{c}\right)\right\}^{\mathrm{2}} \\ $$$$\:\:=\left(\mathrm{1}+{c}\right)^{\mathrm{2}} \left\{\mathrm{2}\left({m}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right\}{x}^{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$\left(\mathrm{1}+{c}\right)\left(\mathrm{1}+{m}\right)={A} \\ $$$$\left(\frac{\mathrm{1}−{c}}{\mathrm{2}+{m}}\right)={B} \\ $$$$\left(\frac{\mathrm{1}+{c}}{\mathrm{2}+{m}}\right)^{\mathrm{2}} \left\{\mathrm{2}\left({m}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right\}={C} \\ $$$$\left({x}+{A}\right)^{\mathrm{2}} \left({x}+{B}\right)^{\mathrm{2}} ={Cx}^{\mathrm{2}} \\ $$$${differentiating} \\ $$$$\left(\frac{{dA}}{{dm}}\right)\left({x}+{A}\right)\left({x}+{B}\right)^{\mathrm{2}} +\left(\frac{{dB}}{{dm}}\right)\left({x}+{B}\right)\left({x}+{A}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\frac{{dC}}{{dm}} \\ $$$$\Rightarrow\:\:\frac{{dA}}{{x}+{A}}+\frac{{dB}}{{x}+{B}}=\frac{{dC}}{\mathrm{2}{C}} \\ $$$$………………………………………. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *