Question Number 27815 by goswamisubhabrata007@gmail.com last updated on 15/Jan/18
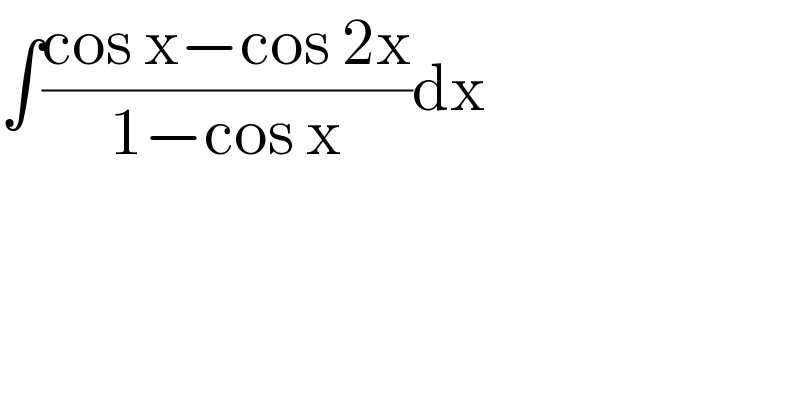
$$\int\frac{\mathrm{cos}\:\mathrm{x}−\mathrm{cos}\:\mathrm{2x}}{\mathrm{1}−\mathrm{cos}\:\mathrm{x}}\mathrm{dx} \\ $$
Answered by ajfour last updated on 15/Jan/18
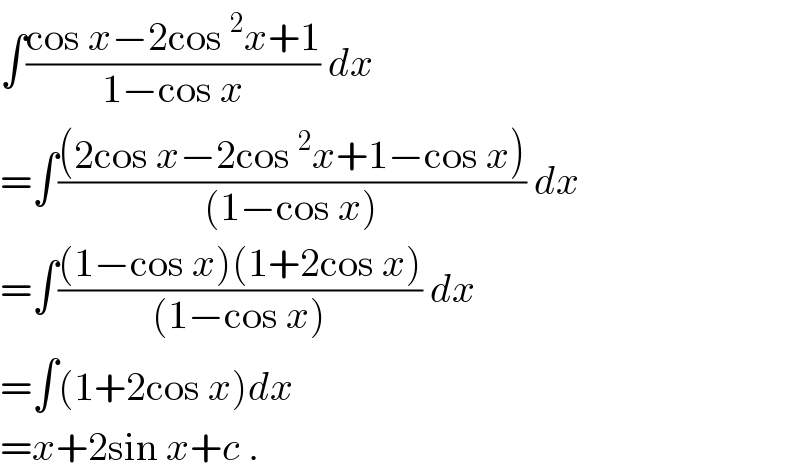
$$\int\frac{\mathrm{cos}\:{x}−\mathrm{2cos}\:^{\mathrm{2}} {x}+\mathrm{1}}{\mathrm{1}−\mathrm{cos}\:{x}}\:{dx} \\ $$$$=\int\frac{\left(\mathrm{2cos}\:{x}−\mathrm{2cos}\:^{\mathrm{2}} {x}+\mathrm{1}−\mathrm{cos}\:{x}\right)}{\left(\mathrm{1}−\mathrm{cos}\:{x}\right)}\:{dx} \\ $$$$=\int\frac{\left(\mathrm{1}−\mathrm{cos}\:{x}\right)\left(\mathrm{1}+\mathrm{2cos}\:{x}\right)}{\left(\mathrm{1}−\mathrm{cos}\:{x}\right)}\:{dx} \\ $$$$=\int\left(\mathrm{1}+\mathrm{2cos}\:{x}\right){dx} \\ $$$$={x}+\mathrm{2sin}\:{x}+{c}\:. \\ $$
