Menu Close

given-that-is-a-real-number-use-mathematical-induction-or-otherwise-to-show-that-cos-2-cos-2-2-cos-2-3-cos-2-n-sin-2-n-sin-2-n-hence-find-the-lim-n-

Tinku Tara 0 Comments
Pin




Question Number 93365 by Rio Michael last updated on 12/May/20
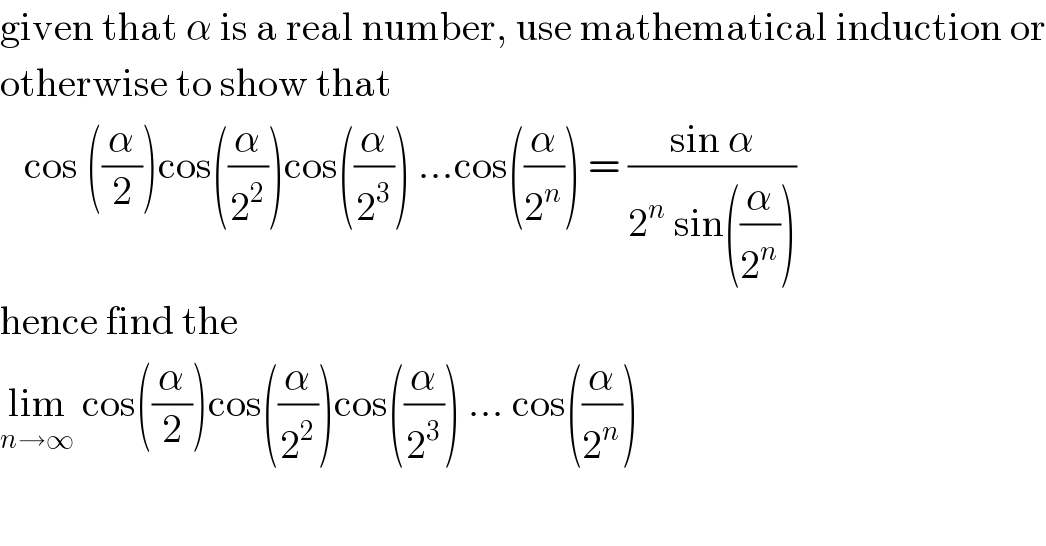
given that α is a real number, use mathematical induction or otherwise to show that cos ((α/2))cos((α/2^2 ))cos((α/2^3 )) ...cos((α/2^n )) = ((sin α)/(2^n sin((α/2^n )))) hence find the lim_(n→∞) cos((α/2))cos((α/2^2 ))cos((α/2^3 )) ... cos((α/2^n ))
$$\mathrm{given}\:\mathrm{that}\:\alpha\:\mathrm{is}\:\mathrm{a}\:\mathrm{real}\:\mathrm{number},\:\mathrm{use}\:\mathrm{mathematical}\:\mathrm{induction}\:\mathrm{or} \\ $$$$\mathrm{otherwise}\:\mathrm{to}\:\mathrm{show}\:\mathrm{that}\: \\ $$$$\:\:\:\mathrm{cos}\:\left(\frac{\alpha}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{\mathrm{2}} }\right)\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{\mathrm{3}} }\right)\:…\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right)\:=\:\frac{\mathrm{sin}\:\alpha}{\mathrm{2}^{{n}} \:\mathrm{sin}\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right)} \\ $$$$\mathrm{hence}\:\mathrm{find}\:\mathrm{the}\: \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{\mathrm{2}} }\right)\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{\mathrm{3}} }\right)\:…\:\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right) \\ $$
Commented by mr W last updated on 12/May/20
P=cos ((α/2))cos((α/2^2 ))cos((α/2^3 )) ...cos((α/2^n )) P 2 sin ((α/2^n ))=cos ((α/2))cos((α/2^2 ))cos((α/2^3 )) ...cos((α/2^n ))2 sin ((α/2^n )) P 2 sin ((α/2^n ))=cos ((α/2))cos((α/2^2 ))cos((α/2^3 )) ...cos((α/2^(n−1) )) sin ((α/2^n )) P 2^2 sin ((α/2^n ))=cos ((α/2))cos((α/2^2 ))cos((α/2^3 )) ...cos((α/2^(n−1) ))2 sin ((α/2^n )) P 2^2 sin ((α/2^n ))=cos ((α/2))cos((α/2^2 ))cos((α/2^3 )) ...cos((α/2^(n−2) ))sin ((α/2^(n−1) )) P 2^3 sin ((α/2^n ))=cos ((α/2))cos((α/2^2 ))cos((α/2^3 )) ...sin ((α/2^(n−2) )) ...... P 2^(n−1) sin ((α/2^n ))=cos ((α/2))sin ((α/2)) P 2^n sin ((α/2^n ))=cos ((α/2))2 sin ((α/2)) P 2^n sin ((α/2^n ))=sin (α) ⇒P=((sin (α))/(2^n sin ((α/2^n )))) ⇒lim_(n→∞) P=((sin (α))/α)×((((α/2^n )))/(sin ((α/2^n ))))=((sin (α))/α)
$${P}=\mathrm{cos}\:\left(\frac{\alpha}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{\mathrm{2}} }\right)\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{\mathrm{3}} }\right)\:…\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right) \\ $$$${P}\:\mathrm{2}\:\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right)=\mathrm{cos}\:\left(\frac{\alpha}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{\mathrm{2}} }\right)\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{\mathrm{3}} }\right)\:…\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right)\mathrm{2}\:\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right) \\ $$$${P}\:\mathrm{2}\:\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right)=\mathrm{cos}\:\left(\frac{\alpha}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{\mathrm{2}} }\right)\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{\mathrm{3}} }\right)\:…\mathrm{co}{s}\left(\frac{\alpha}{\mathrm{2}^{{n}−\mathrm{1}} }\right)\:\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right) \\ $$$${P}\:\mathrm{2}^{\mathrm{2}} \:\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right)=\mathrm{cos}\:\left(\frac{\alpha}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{\mathrm{2}} }\right)\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{\mathrm{3}} }\right)\:…\mathrm{co}{s}\left(\frac{\alpha}{\mathrm{2}^{{n}−\mathrm{1}} }\right)\mathrm{2}\:\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right) \\ $$$${P}\:\mathrm{2}^{\mathrm{2}} \:\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right)=\mathrm{cos}\:\left(\frac{\alpha}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{\mathrm{2}} }\right)\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{\mathrm{3}} }\right)\:…\mathrm{co}{s}\left(\frac{\alpha}{\mathrm{2}^{{n}−\mathrm{2}} }\right)\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}^{{n}−\mathrm{1}} }\right) \\ $$$${P}\:\mathrm{2}^{\mathrm{3}} \:\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right)=\mathrm{cos}\:\left(\frac{\alpha}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{\mathrm{2}} }\right)\mathrm{cos}\left(\frac{\alpha}{\mathrm{2}^{\mathrm{3}} }\right)\:…\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}^{{n}−\mathrm{2}} }\right) \\ $$$$…… \\ $$$${P}\:\mathrm{2}^{{n}−\mathrm{1}} \:\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right)=\mathrm{cos}\:\left(\frac{\alpha}{\mathrm{2}}\right)\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}}\right) \\ $$$${P}\:\mathrm{2}^{{n}} \:\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right)=\mathrm{cos}\:\left(\frac{\alpha}{\mathrm{2}}\right)\mathrm{2}\:\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}}\right) \\ $$$${P}\:\mathrm{2}^{{n}} \:\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right)=\mathrm{sin}\:\left(\alpha\right) \\ $$$$\Rightarrow{P}=\frac{\mathrm{sin}\:\left(\alpha\right)}{\mathrm{2}^{{n}} \mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right)} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}{P}=\frac{\mathrm{sin}\:\left(\alpha\right)}{\alpha}×\frac{\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right)}{\mathrm{sin}\:\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right)}=\frac{\mathrm{sin}\:\left(\alpha\right)}{\alpha} \\ $$
Commented by Rio Michael last updated on 12/May/20
perfect sir
$$\mathrm{perfect}\:\mathrm{sir} \\ $$
Commented by Rio Michael last updated on 12/May/20
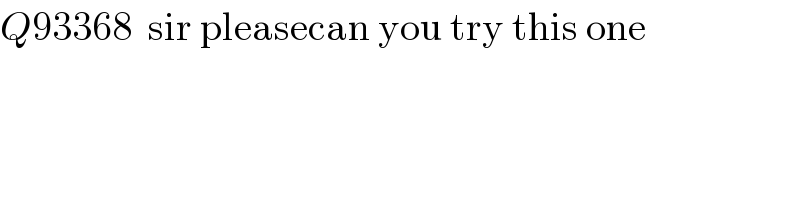
Q93368 sir pleasecan you try this one
$${Q}\mathrm{93368}\:\:\mathrm{sir}\:\mathrm{pleasecan}\:\mathrm{you}\:\mathrm{try}\:\mathrm{this}\:\mathrm{one} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *