Menu Close

Let-z-and-w-be-two-complex-numbers-such-that-z-1-w-1-and-z-iw-z-iw-2-then-find-the-value-of-z-

Tinku Tara
Pin




Question Number 230 by ssahoo last updated on 25/Jan/15
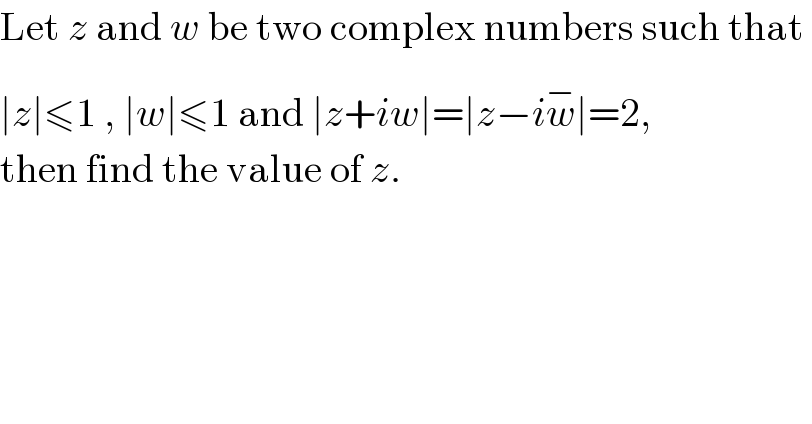
Let z and w be two complex numbers such that ∣z∣≤1 , ∣w∣≤1 and ∣z+iw∣=∣z−iw^(−) ∣=2, then find the value of z.
$$\mathrm{Let}\:{z}\:\mathrm{and}\:{w}\:\mathrm{be}\:\mathrm{two}\:\mathrm{complex}\:\mathrm{numbers}\:\mathrm{such}\:\mathrm{that}\: \\ $$$$\mid{z}\mid\leqslant\mathrm{1}\:,\:\mid{w}\mid\leqslant\mathrm{1}\:\mathrm{and}\:\mid{z}+{iw}\mid=\mid{z}−{i}\overline {{w}}\mid=\mathrm{2}, \\ $$$$\mathrm{then}\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{z}. \\ $$
Commented by 123456 last updated on 16/Dec/14
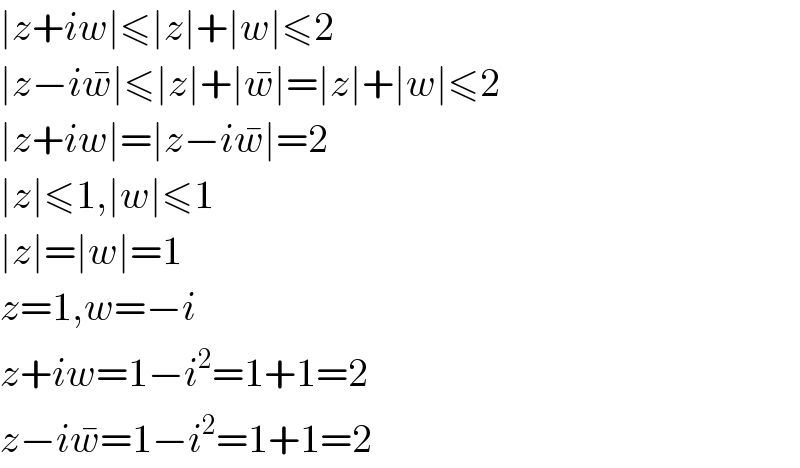
∣z+iw∣≤∣z∣+∣w∣≤2 ∣z−iw^� ∣≤∣z∣+∣w^� ∣=∣z∣+∣w∣≤2 ∣z+iw∣=∣z−iw^� ∣=2 ∣z∣≤1,∣w∣≤1 ∣z∣=∣w∣=1 z=1,w=−i z+iw=1−i^2 =1+1=2 z−iw^� =1−i^2 =1+1=2
$$\mid{z}+{iw}\mid\leqslant\mid{z}\mid+\mid{w}\mid\leqslant\mathrm{2} \\ $$$$\mid{z}−{i}\bar {{w}}\mid\leqslant\mid{z}\mid+\mid\bar {{w}}\mid=\mid{z}\mid+\mid{w}\mid\leqslant\mathrm{2} \\ $$$$\mid{z}+{iw}\mid=\mid{z}−{i}\bar {{w}}\mid=\mathrm{2} \\ $$$$\mid{z}\mid\leqslant\mathrm{1},\mid{w}\mid\leqslant\mathrm{1} \\ $$$$\mid{z}\mid=\mid{w}\mid=\mathrm{1} \\ $$$${z}=\mathrm{1},{w}=−{i} \\ $$$${z}+{iw}=\mathrm{1}−{i}^{\mathrm{2}} =\mathrm{1}+\mathrm{1}=\mathrm{2} \\ $$$${z}−{i}\bar {{w}}=\mathrm{1}−{i}^{\mathrm{2}} =\mathrm{1}+\mathrm{1}=\mathrm{2} \\ $$
Answered by prakash jain last updated on 16/Dec/14
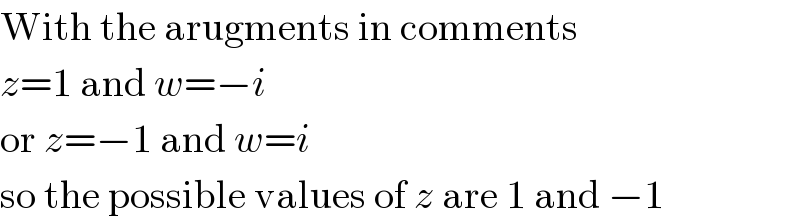
With the arugments in comments z=1 and w=−i or z=−1 and w=i so the possible values of z are 1 and −1
$$\mathrm{With}\:\mathrm{the}\:\mathrm{arugments}\:\mathrm{in}\:\mathrm{comments} \\ $$$${z}=\mathrm{1}\:\mathrm{and}\:{w}=−{i} \\ $$$$\mathrm{or}\:{z}=−\mathrm{1}\:\mathrm{and}\:{w}={i} \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{possible}\:\mathrm{values}\:\mathrm{of}\:{z}\:\mathrm{are}\:\mathrm{1}\:\mathrm{and}\:−\mathrm{1} \\ $$

Pin